Inferência Causal

Propensity Score

Prof. Carlos Trucíos
ctrucios@unicamp.br

Instituto de Matemática, Estatística e Computação Científica (IMECC),
Universidade Estadual de Campinas (UNICAMP).

Introdução

Introdução

  • Introduzido por Rosembaum e Rubin (1983), propensity score desempenha um papel crucial na inferência causal quando trabalhamos com estudos observacionais.
  • Propensity score é uma ferramenta importante na inferência causal. O foco da aula de hoje está em entender o motivo pelo qual é tão importante.

Propensity score

Propensity score

Assumindo uma amostragem IID, temos quatro variáveis aleatórias associadas a cada unidade \(i\):

  • \(X\),
  • \(Z\),
  • \(Y(1)\) e
  • \(Y(0)\).

Ademais, \[\begin{align} P(X, Z, Y(1), Y(0)) &= P(Z, Y(1), Y(0) | X) \times P(X), \\ &= P(Z | X, Y(1), Y(0)) \times P(Y(1), Y(0) | X) \times P(X) \end{align}\]

Propensity score

Definição (Propensity score):

Definimos \[e(X, Y(1), Y(0)) = P(Z = 1| X, Y(1), Y(0))\] como o propensity score. Sob ignorabilidade forte, \[e(X, Y(1), Y(0)) = P(Z = 1| X, Y(1), Y(0)) = P(Z = 1 | X)\] que é simplesmente denotado por \(e(X)\) e é a probabilidade condicional de receber o tratamento dado as covariáveis observadas

\(e(X)\) apresenta uma série de propriedades que serão bastante úteis para inferirmos causalidade.

Propensity Score: Redução de Dimensão

Propensity Score: Redução de Dimensão

Teorema

Se \(Z \perp\!\!\!\perp \{ Y(1), Y(0)\} | X\), então \(Z \perp\!\!\!\perp \{ Y(1), Y(0)\} | e(X)\)

  • O Teorema estabelece que, se ignorabilidade forte acontece (dado \(X\)), também acontece dado \(e(X)\).
  • Isto implica que condicionar em \(e(X)\) remove qualquer efeito confundidor induzido por \(X\).
  • \(X\) pode ser geral e multidimensional, já \(e(X)\) é unidimensional e está entre 0 e 1.
  • Então, propensity score reduz a dimensão das covariáveis originais mas ainda mantem a ignorabilidade.
  • Demostração (no quadro)

Propensity Score: Redução de Dimensão

O Teorema anterior motiva um método para estimar efeitos causais: Propensity Score Stratification.

  • Assuma que o propensity score é conhecido e com apenas \(K\) (\(K << n\)) possíveis valores \(\{e_1, e_2, \cdots, e_K \}\).
  • Neste caso, o Teorema anterior pode ser re-escrito como \[Z \perp\!\!\!\perp \{ Y(1), Y(0)\} | e(X) = e_k \quad (k = 1, \cdots, K).\]
  • Assim, temos um SRE, o que implica em \(K\) CRES independentes em cada estrato do propensity score e podemos analizar os dados observacionais da mesma forma como no SRE (mas agora estratificado em \(e(X)\)) 😄

Propensity Score: Redução de Dimensão

Na prática, \(e(X)\) não é conhecido e não é discreto 😭.

E agora?

  • Ajustamos um modelo para \(P(Z = 1 | X)\), por exemplo, um modelo logístico.
  • Os valores ajustados serão os propensity score estimados, \(\hat{e}(X)\).
  • \(\hat{e}(X)\) não precisa ser discreto (de fato pode assumir tanto valores quantas observações disponíveis) 😢.
  • Contudo, podemos discretizar (utilizando os quantis ou algum outro método) \(\hat{e}(X)\) e termos (aproximadamente) \[Z \perp\!\!\!\perp \{ Y(1), Y(0)\} | \hat{e}'(X) = e_k \quad (k = 1, \cdots, K),\] em que \(\hat{e}'(X)\) são os valores discretizados 😄.

Propensity Score: Redução de Dimensão

  • Para obtermos \(\hat{e}(X)\) precisamos ajustar um modelo, o que nos leva a pensar se o estimador final é dependente do modelo escolhido.
  • Note que a estratificação utilizando propensity score apenas precisa que a ordem esteja correta em lugar do que seus valores exatos.
  • Isto torna o método (um pouco) robusto à escolha do modelo.

Propensity Score: Redução de Dimensão

Como escolher \(K\)?
  • Rosenbaum and Rubin (1984) sugerem \(K = 5\).
  • Wang et al. (2020) sugerem escolher \(K\) como o máximo número de estratos nos quais o estimador estratificado está bem definido.
Como calcular o desvio padrão?
  • Alguns autores calculam o desvio padrão dentro de cada estrato obtido atraves de \(\hat{e}(X)\), mas a incerteza associada a \(\hat{e}(X)\) não é levada em consideração.
  • Outros preferem fazer um Bootstrap para levar em consideração a incerteza associada a \(\hat{e}(X)\).

Propensity Score: Redução de Dimensão

Exemplo

Dataset disponível aqui. Chang et al. (2016) estudam se a participação no programa da merenda nas escolas (School_meal) leva a um aumento no índice de massa muscular (BMI) das crianças. 12 outras covariáveis também estão disponíveis no dataset.

Code 
dados <- read.csv("datasets/nhanes_bmi.csv")[, -1]
z <- dados$School_meal
y <- dados$BMI
x <- scale(dados[, -c(1, 2)])

Calculamos \(\hat{e}(X)\)

Code 
prop_score <- glm(z ~ x, family = binomial)$fitted.values

Propensity Score: Redução de Dimensão

Estratificamos e estimamos o efeito causal médio.

Code 
neyman_sre <- function(y, z, x) {
  x_levels <- unique(x)
  K <- length(x_levels)
  pi_k <- rep(0, K)
  tau_k <- rep(0, K)
  v_k <- rep(0, K)
  n <- length(z)
  for (k in 1:K) {
    x_k <- x_levels[k]
    z_k <- z[x == x_k]
    y_k <- y[x == x_k]
    pi_k[k] <- length(z_k)/n
    tau_k[k] <- mean(y_k[z_k == 1]) - mean(y_k[z_k == 0])
    v_k[k] <- var(y_k[z_k == 1]) / sum(z_k) + var(y_k[z_k == 0]) / sum(1 - z_k)
  }
  tau_s <- sum(pi_k * tau_k)
  v_s <- sum(pi_k^2 * v_k) 
  return(c(tau_s, sqrt(v_s)))
}

K <- c(5, 10, 20, 50, 80)
resultados <- sapply(K, FUN = function(k){
                          q_prop_score = quantile(prop_score, (1:(k - 1))/k)
                          ps_estrato = cut(prop_score, breaks = c(0, q_prop_score, 1), labels = 1:k)
                          neyman_sre(y, z, ps_estrato)
                          })
colnames(resultados) <- K
rownames(resultados) <- c("Estim", "SE")
resultados
               5         10         20         50         80
Estim -0.1160964 -0.1776036 -0.1996877 -0.2647423 -0.2037701
SE     0.2833304  0.2824724  0.2789719  0.2724072         NA

Propensity Score: Redução de Dimensão

Como seriam os resultados se não utilizamos propensity score?

Code 
library(car)
naive <- lm(y ~ z)
fisher <- lm(y ~ z + x)
lin <- lm(y ~ z*x)
resultados <- matrix(c(coef(naive)[2], sqrt(hccm(naive)[2, 2]),
                       coef(fisher)[2], sqrt(hccm(fisher)[2, 2]),
                       coef(lin)[2], sqrt(hccm(lin)[2, 2])), ncol = 3)
colnames(resultados) <- c("Naive", "Fisher", "Lin")
rownames(resultados) <- c("Estim", "SE")
resultados
          Naive     Fisher         Lin
Estim 0.5339044 0.06124785 -0.01695389
SE    0.2254186 0.22673582  0.22587296

O estimador de Lin e o método de propensity score stratification fornecem, qualitativamente, os mesmo resultados. Já o estimador Naive difere bastante dos outros métodos (Why?) enquanto que Fisher devolve um efeito positivo, porém, insignificante.

Propensity Score: Redução de Dimensão

Code 
mahalanobis2 = function(z, x) {
  x1 <- x[z == 1, ]
  x0 <- x[z == 0, ]
  n1 <- nrow(x1)
  n0 <- nrow(x0)
  diff <- apply(x1, 2, mean) - apply(x0, 2, mean)
  covar <- (n1 + n0)/(n1 * n0) * cov(x)
  M <- t(diff) %*% solve(covar) %*% diff
  return(M)
}
mahalanobis2(z, x)
         [,1]
[1,] 619.0012

O (alto) nível de desbalanceameto explica o motivo pelo qual o método Naive difere tanto dos outros métodos.

Propensity Score: Ponderação

Propensity Score: Ponderação

Teorema

Se \(Z \perp\!\!\!\perp \{ Y(1), Y(0)\} | X\) e \(0 < e(X) < 1\), então: \[\mathbb{E}[Y(1)] = \mathbb{E} \Big [ \dfrac{ZY}{e(X)}\Big], \quad \mathbb{E}[Y(0)] = \mathbb{E} \Big [ \dfrac{(1 - Z)Y}{1 - e(X)}\Big] \quad e\] \[\tau = \mathbb{E}[Y(1) - Y(0)] = \mathbb{E} \Big [\dfrac{ZY}{e(X)} - \dfrac{(1-Z)Y}{1-e(X)} \Big]\]

Demostração (no quadro)

Estimador IPW

O estimador IPW (Inverse Propensity Score Weighting), também conhecido como estimador HT (Horvitz-Thompson) é motivado pelo Teorema anterior e é dado por \[\hat{\tau}^{IPW} = \dfrac{1}{n} \displaystyle \sum_{i = 1}^n \dfrac{Z_i Y_i}{\hat{e}(X_i)} - \dfrac{1}{n} \displaystyle \sum_{i = 1}^n \dfrac{(1 - Z_i)Y_i}{1- \hat{e}(X_i)},\] em que \(\hat{e}(X_i)\) é o propensity score estimado.

Estimador IPW

  • Suponha que em lugar de termos resultado observado \(Y_i\), temos \(\tilde{Y}_i = Y_i + c\) (\(\forall i\)).
  • Adicionar, para cada \(i\), uma constante ao resultado observado não deveria mudar o efeito causal médio.
  • Contudo, se adicionarmos, para cada \(i\), uma constante \(c\), temos que \(\hat{\tau}^{IPW}\) torna-se \[\hat{\tau}^{IPW} + c \Big[\dfrac{1}{n} \displaystyle \sum_{i = 1}^n \dfrac{Z_i}{\hat{e}(X_i)} - \dfrac{1}{n} \displaystyle \sum_{i = 1}^n \dfrac{1 - Z_i}{1 - \hat{e}(X_i)} \Big]\]

O estimador \(\hat{\tau}^{IPW}\) apresenta um sério problema: não é invariante a transformações de locação de \(Y\) 🙍.

Estimador IPW

  • \(\hat{\tau}^{IPW}\) não é um estimador razoável, pois depende de \(c\).
  • Uma forma simples de remediar o problema é normalizar os pesos. Este estimador é conhecido como o estimador de Hajek e é dado por \[\hat{\tau}^{Hajek} = \dfrac{\displaystyle \sum_{i = 1}^n \dfrac{Z_i Y_i}{\hat{e}(X_i)}}{\displaystyle \sum_{i = 1}^n \dfrac{Z_i}{\hat{e}(X_i)}} - \dfrac{\displaystyle \sum_{i = 1}^n \dfrac{(1 - Z_i)Y_i}{1- \hat{e}(X_i)}}{\displaystyle \sum_{i = 1}^n \dfrac{1 - Z_i}{1- \hat{e}(X_i)}}.\]
  • Pode-se mostrar que \(\hat{\tau}^{Hajek}\) é invariante a transformações de locação 😄.

Estimador IPW

  • Muitos resultados assintóticos requerem que \(0 < \alpha_L <e(X) < \alpha_U < 1\) (condicação conhecida como sobreposição forte).
  • Contudo, esta suposição é bastante forte (D’Amour et al. 2021) e mesmo se a condição é verificada para \(e(X)\) não há garantia que seja verificada para \(\hat{e}(X)\) (o que permite que o estimador exploda, tornando os resultados bastante instáveis).
  • Para evitar isto, podemos: substituir \(\hat{e}(X)\) por \(\max [\alpha_L, \min[\hat{e}(X_i), \alpha_U]]\).
  • Algumas escolhas comuns para \(\alpha_L\) e \(\alpha_U\) são 0.1 e 0.9 ou 0.05 e 0.95.

Estimador IPW

Implementação

Code 
estimador_ipw <- function(z, y, x, alphas = c(0, 1)) {
  prop_score <- glm(z ~ x, family = binomial)$fitted.values
  prop_score <- pmax(alphas[1], pmin(prop_score, alphas[2]))
  
  tau_ipw <- mean(z * y / prop_score) - mean((1 - z) * y / (1 - prop_score))
  tau_hajek <- mean(z * y / prop_score) / mean(z / prop_score) - mean((1 - z) * y / (1 - prop_score)) / mean((1 - z) / (1 - prop_score))
  
  out <- c(tau_ipw, tau_hajek)
  return(out)
}

Estimador IPW

Implementação

Code 
bootstrap_ipw <- function(z, y, x, n_boot = 500, alphas = c(0, 1)) {
  poit_estim <- estimador_ipw(z, y, x, alphas)
  
  n <- length(z)
  boot_estim <- replicate(n_boot, {
    sample_boot <- sample(1:n, n, replace = TRUE)
    estimador_ipw(z[sample_boot], y[sample_boot], x[sample_boot, ], alphas)
  })
  boot_se <- apply(boot_estim, 1, sd)
  out <- cbind(poit_estim, boot_se)
  colnames(out) <- c("Est", "SD")
  rownames(out) <- c("IPW", "Hajek")
  return(out)
}

Estimador IPW

Exemplo (Merenda e BMI)

Chang et al. (2016) estudam se a participação no programa da merenda nas escolas (School_meal) leva a um aumento no índice de massa muscular (BMI) das crianças. 12 outras covariáveis também estão disponíveis no dataset.

Code 
dados <- read.csv("datasets/nhanes_bmi.csv")[, -1]
z <- dados$School_meal
y <- dados$BMI
x <- scale(dados[, -c(1, 2)])

A maneira de exemplo, utilizaremos diversos valores de \(\alpha_L\) e \(\alpha_U\):

  • (0, 1)
  • (0.01, 0.99)
  • (0.05, 0.95)
  • (0.1, 0.9)

Estimador IPW

Exemplo (Merenda e BMI)

Code 
l_alphas <- list(alpha_01 = c(0, 1), alpha_02 = c(0.01, 0.99),
               alpha_03 = c(0.05, 0.95), alpha_04 = c(0.1, .9))

trim_estim <- lapply(l_alphas, 
                     function(a) {round(bootstrap_ipw(z, y, x, alphas = a), 3)} )
trim_estim
$alpha_01
         Est    SD
IPW   -1.516 0.481
Hajek -0.156 0.242

$alpha_02
         Est    SD
IPW   -1.516 0.487
Hajek -0.156 0.239

$alpha_03
         Est    SD
IPW   -1.499 0.460
Hajek -0.152 0.244

$alpha_04
         Est    SD
IPW   -0.713 0.411
Hajek -0.054 0.231
  • Note que o estimador de Hajek é sempre negativo e insignificante.
  • O estimador de HW (IPW) é bastante negativo e, dependendo do truncamento, significativo.
  • O estimador de HW é instável e devemos preferir Hajek!

Propensity Score: Balanceamento

Propensity Score: Balanceamento

Teorema

O propensity score satisfaz \[Z \perp\!\!\!\perp X | e(X).\] Ademais, para qualquer função \(h(\cdot)\), temos que \[\mathbb{E} \Big [\dfrac{Zh(X)}{e(X)} \Big] = \mathbb{E} \Big[\dfrac{(1 - Z) h(X)}{1- e(X)} \Big],\] desde que ambas as \(\mathbb{E}(\cdot)\) existam.

O que significa essa teorema?
  • Condicional no propensity score, a indicadora de tratamento e as covariáveis são independentes.
  • Portanto, dentro de cada nível do propensity score, a distribuição das covariáveis é balanceada entre tratamento e controle.

Propensity Score: Balanceamento

  • O Teorema anterior tem uma implicação direta na análise de dados.
  • Antes de termos acesso aos resultados (\(Y\)), podemos verificar se o modelo de propensity score está bem especificado como para garantir o balanceamento das covariáveis.
  • Por exemplo, pense no propensity score stratification. Discretizamos \(\hat{e}(X)\) para termos \(\hat{e}'(X)\) e então, aproximadamente \[Z \perp\!\!\!\perp X | \hat{e}'(X) = e_k \quad (k = 1, \cdots, K).\] Assim, podemos verificar se a distribuição das covariáveis é a mesma entre tratamento e controle dentro de cada estrato.

Propensity Score: Balanceamento

Code 
library(ggplot2)
balance_check <- sapply(1:ncol(x),
                FUN = function(px){
                  q_prop_score = quantile(prop_score, (1:4)/5)
                  prop_score_strata = cut(prop_score, breaks = c(0, q_prop_score, 1), labels = 1:5)
                  neyman_sre(x[, px], z, prop_score_strata)
                })

dat_balance <- data.frame(est = balance_check[1, ],
                         upper = balance_check[1, ] + 1.96*balance_check[2, ],
                         lower = balance_check[1, ] - 1.96*balance_check[2, ],
                         cov = factor(1:11))
ggplot(dat_balance) + 
  geom_errorbar(aes(x = cov, ymin = lower, ymax = upper), alpha = 0.6) + 
  geom_point(aes(x = cov, y = est), alpha = 0.6) +
  geom_hline(aes(yintercept = 0), alpha = 0.3) + 
  theme_bw() + 
  theme(panel.grid.major = element_blank(),
        panel.grid.minor = element_blank(),
        axis.title.y = element_blank()) +
  xlab("Verificando balanceamento com base na estratificação (K = 5)")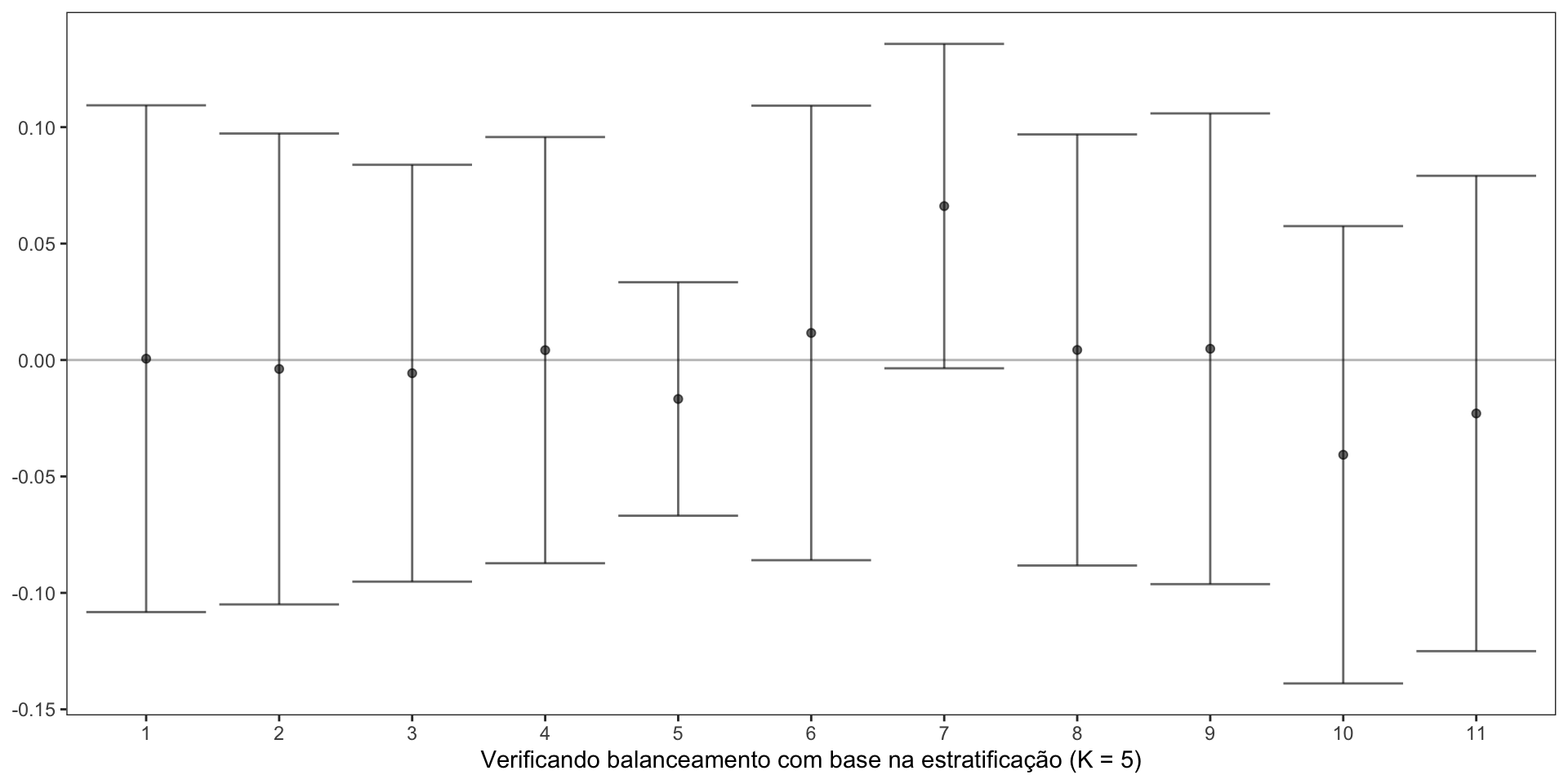

Propensity Score: Balanceamento

Code 
balance_check <- sapply(1:dim(x)[2],
                FUN = function(px){
                  bootstrap_ipw(z, x[, px], x)[2, ]
                })

dat_balance <- data.frame(est = balance_check[1, ],
                         upper = balance_check[1, ] + 1.96*balance_check[2, ],
                         lower = balance_check[1, ] - 1.96*balance_check[2, ],
                         cov = factor(1:11))
ggplot(dat_balance) + 
  geom_errorbar(aes(x = cov, ymin = lower, ymax = upper), alpha = 0.6) + 
  geom_point(aes(x = cov, y = est), alpha = 0.6) +
  geom_hline(aes(yintercept = 0), alpha = 0.3) + 
  theme_bw() + 
  theme(panel.grid.major = element_blank(),
        panel.grid.minor = element_blank(),
        axis.title.y=element_blank()) +
  xlab("balance check based on weighting")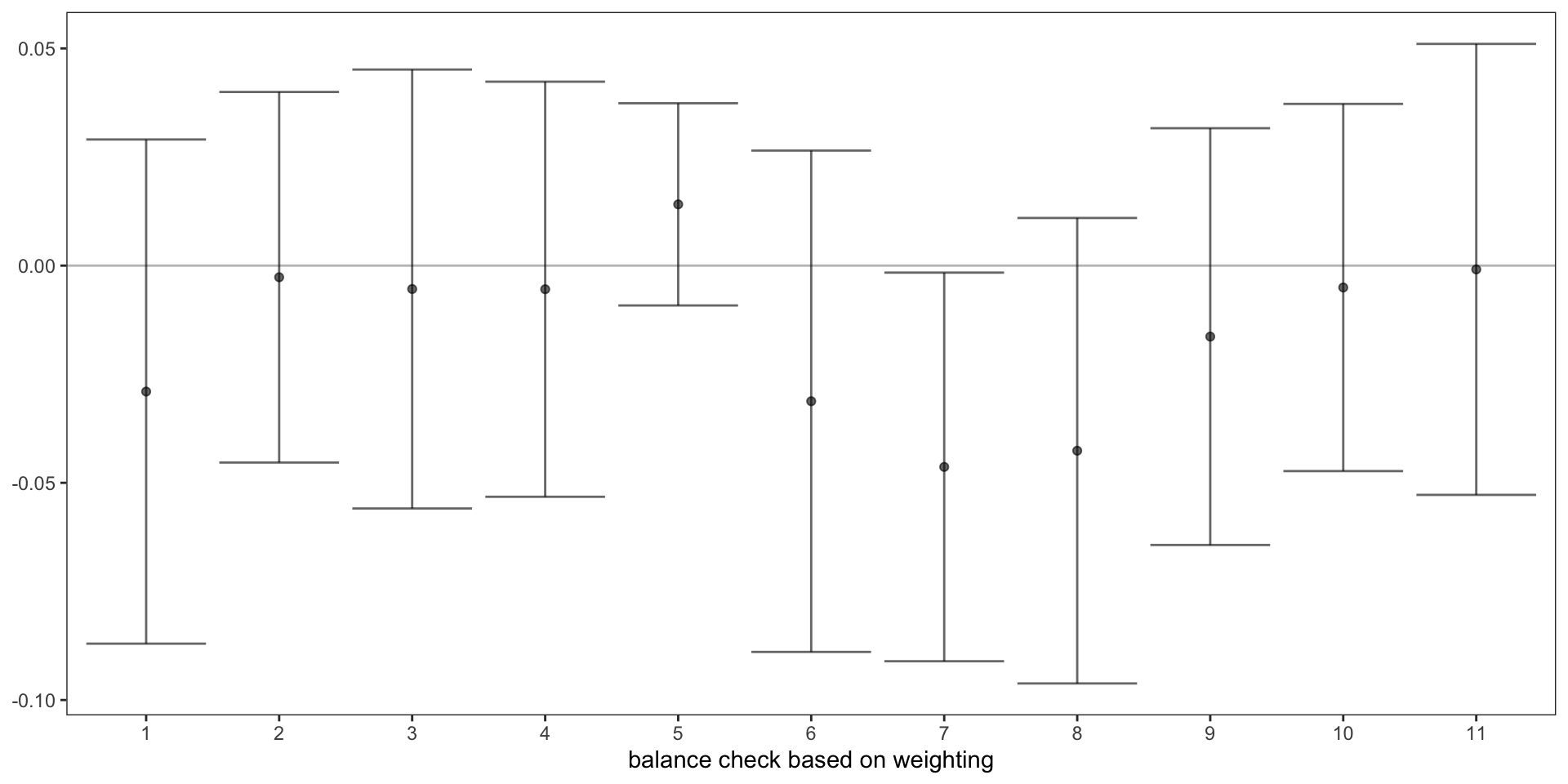

Referências

  • Peng Ding (2023). A First Course in Causal Inference. Capítulo 11.

Carlos Trucíos (IMECC/UNICAMP) | ME920/MI628 - Inferência Causal | ctruciosm.github.io