Experimentos Randomizados: comentários finais
Instituto de Matemática, Estatística e Computação Científica (IMECC),
Universidade Estadual de Campinas (UNICAMP).
Existem diversas escolhas de estatística de teste para o FRT. Contudo, existe uma vantagem de se utilizar a estatística \(t\) Studentizada, \[t = \dfrac{\hat{\tau}}{\sqrt{\hat{V}}}.\]
Resultado
Ding e Dasgupta (2017) mostram que o FRT com estatística \(t\) Studentizada fornece:
Importante
Seja
\[t = \dfrac{\hat{\tau}}{\sqrt{\hat{V}}} = \dfrac{\sqrt{\mathbb{V}(\hat{\tau})}}{\sqrt{\hat{V}}} \dfrac{\hat{\tau}}{\sqrt{\mathbb{V}(\hat{\tau})}},\]
Em que \(C \leq 1\), com a igualdade acontecendo se \(\tau_i = \tau, \quad \forall i\).
No caso do FRT, sob \(H_{0F}\), \(Y_i(1) = Y_i(0) = Y_i\), ou seja \(\tau_i = 0, \forall i\). Assim, \[t^{\pi} \xrightarrow D N(0,1),\] em que \(()^{\pi}\) denota a distribuição da permutação aleatória.
library(ggplot2)
a <- seq(-4, 4, by = 0.001)
n <- length(a)
dados <- data.frame(
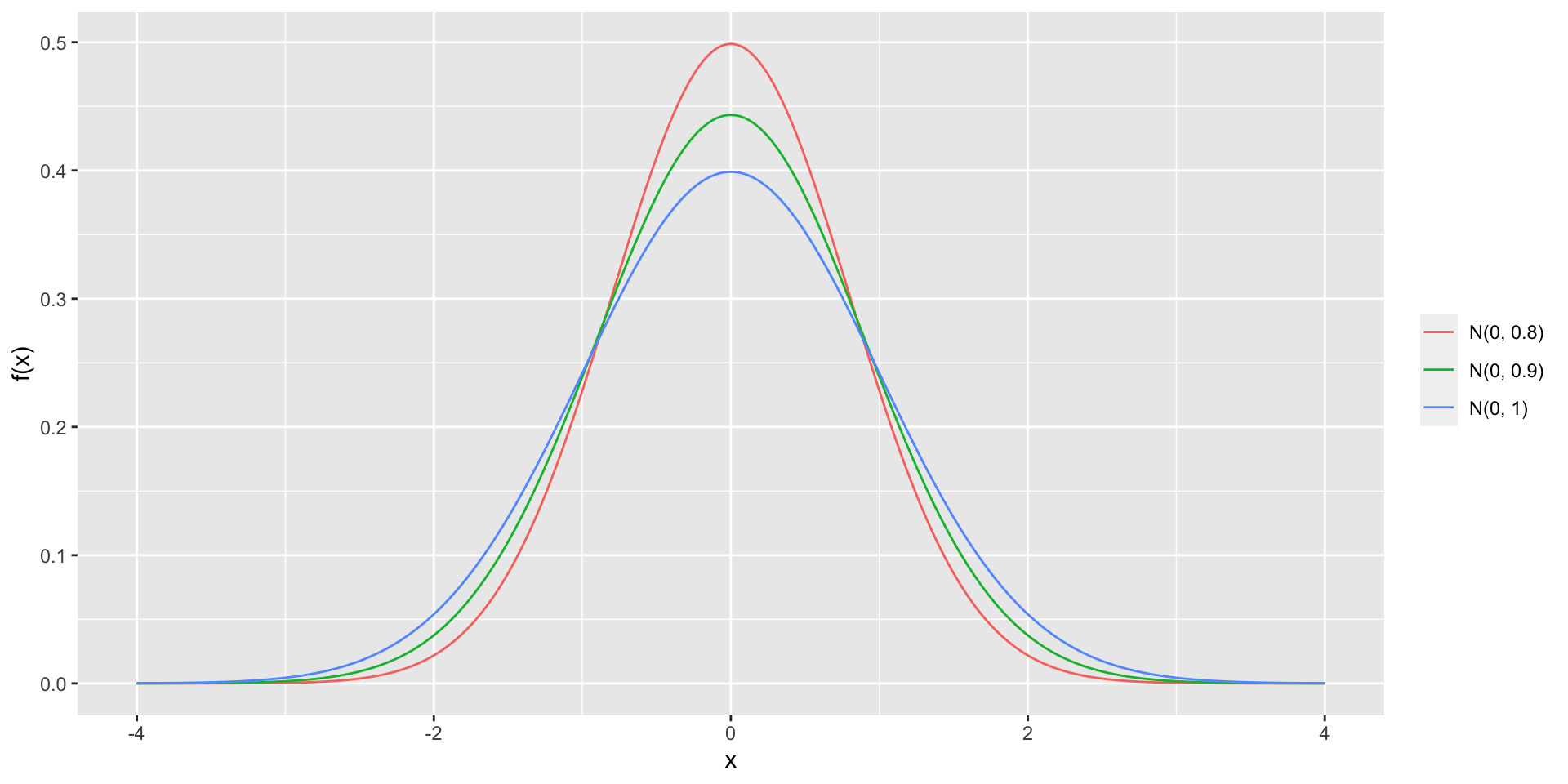
distri = rep(c("N(0, 1)", "N(0, 0.9)", "N(0, 0.8)"), each = n),
x = rep(a, 3),
y = c(dnorm(a), dnorm(a, 0, 0.9), dnorm(a, 0, 0.8)))
ggplot(data = dados) + geom_line(aes(x, y, color = distri)) +
ylab("f(x)") +
theme(legend.title = element_blank()) Como \(N(0,1)\) é mais disperso do que \(N(0,C^2)\), o \(p_{FRT}\) baseado em \(t\) é asintóticamente mais conservador.
De forma semelhante, na presença de covariáveis, Zhao e Ding (2021) recomedam utilizar FRT com \[t_L = \dfrac{\hat{\tau}_L}{\sqrt{\hat{V}_L}},\] em que \(\hat{\tau}_L\) é o estimador de Lin (2013.)
Baseados nos trabalhos de Ding e Dasgupta (2017) e Zhao e Ding (2021), podemos resumir as recomendações em:
| Sem covariável | Com covariável | |
|---|---|---|
| CRE | \(t = \hat{\tau} \big / \sqrt{\hat{V}}\) | \(t_{L} = \hat{\tau}_{L} \big / \sqrt{\hat{V}_{L}}\) |
| SRE | \(t_S = \hat{\tau}_S \big / \sqrt{\hat{V}_S}\) | \(t_{L,S} = \hat{\tau}_{L, S} \big / \sqrt{\hat{V}_{L,S}}\) |
| ReM | \(\times\) | \(t_{L} = \hat{\tau}_{L} \big / \sqrt{\hat{V}_{L}}\) |
Isto todo, traz algumas vantagens:
Contudo, esta abordagem é frequentemente criticada por ter validez interna mas não necessariamente validez externa 😭.
Definição (validez interna)
A análise estatística é valida para a amostra estudada.
Definição (validez externa)
A análise estatística é valida para a amostra estudada mas também para a população de onde a amostra foi extraida.
Sempre estamos interesados em validez externa e não apenas na interna. Contudo, como o arcabouço teórico até aqui construido é condicionado nos resultados potenciais, sob a perspectiva de população finita, os resultados são apenas válidos para a amostra observada.
Note então que precisamos de dois níveis de randomização: (1) do processo de amostragen e (2) do mecanismo de atribuição de tratamento.
Vamos assumir que a amostra foi aleatoriamente selecionada da população de interesse. Assim, todas nossas afirmações são a respeito da população de interesse e não apenas da amostra em estudo.
Vamos assumir que \[\{Z_i, Y_i(1), Y_i(0), X_i \}_{i = 1}^n \overset{IID}{\sim} \{Z, Y(1), Y(0), X\},\] em que temos omitido os subíndices \(i\) na super população.
Definimos o efeito causal médio da população como \[\tau = \mathbb{E}(Y(1) - Y(0)) = \mathbb{E}(Y(1)) - \mathbb{E}(Y(0)).\]
CRE (super população)
\[Z \perp\!\!\!\perp \{Y(1), Y(0), X \}.\]
Sob CRE, o efeito causal médio da população pode ser escrito como \[ \tau = \mathbb{E}(Y(1) | Z = 1) - \mathbb{E}(Y(0) | Z = 0) = \mathbb{E}(Y | Z = 1) - \mathbb{E}(Y | Z = 0) \]
Um estimador de momentos é dado por:
\[\hat{\tau} = {n_1}^{-1} \displaystyle \sum_{i = 1}^{n} Z_i Y_i - {n_0}^{-1} \displaystyle \sum_{i = 1}^{n} (1 - Z_i) Y_i\]
Sob IID, a variância amostral é não viesado para a variância populacional. Ou seja, o estimador (conservador) de Neyman é não viesado para \(\mathbb{V}(\hat{\tau} | textbf{Z})\) (o problema de ser um estimador conservador vá embora quando pensamos em super populações!)
\[\begin{align*} Y(1) & = \delta_1 + \beta_1'X + \varepsilon(1), \\ Y(0) & = \delta_0 + \beta_0'X + \varepsilon(0). \\ \end{align*}\]
\[\tau = \mathbb{E}(Y(1)-Y(0)) = (\delta_1 - \delta_0) + (\beta_1 - \beta_0)' \mathbb{E}(X),\]
E sua versão amostral é \[\hat{\tau}_{adj} = (\hat{\delta}_1 - \hat{\delta}_0) + (\hat{\beta}_1 - \hat{\beta}_0)' \bar{X},\] em que se \(X\) for centrado, temos:
\[\hat{\tau}_{adj} = \hat{\delta}_1 - \hat{\delta}_0 = \hat{\tau}_L,\] em que os coeficientes estimador são todos obtidos por MQO.
Para estimar a variância, precisaremos:
\[\hat{V}_{EHW} + (\hat{\beta}_1 - \hat{\beta}_0)'S_X^2(\hat{\beta}_1 - \hat{\beta}_0)/n,\] em que \((\hat{\beta}_1 - \hat{\beta}_0)\) é o coeficiente da interação \(Z_iX_i\) obtido no estimador de Lin.
Outra opção é fazer bootstrap para estimar a variância.
Ilustração
library(car)
lin_estimator <- function(Z, X, Y) {
X <- scale(X)
n <- length(Y)
p <- ncol(X)
modelo <- lm(Y ~ Z*X)
tau_lin <- coef(modelo)[2]
v_ehw <- hccm(modelo)[2, 2]
aux_beta <- matrix(coef(modelo)[-(1:(p + 2))], ncol = 1)
v_super_pop <- v_ehw + t(aux_beta) %*% cov(X) %*% aux_beta / n
out <- c(tau_lin, sqrt(v_ehw), sqrt(v_super_pop))
return(out)
}Ilustração
Ilustração
[1] 0.001441006[1] 0.152001[1] 0.1388576[1] 0.1532274[1] 0.926[1] 0.9505É possível extender a discusão para o caso de SRE.
Vamos assumir que \[\{Z_i, Y_i(1), Y_i(0), X_i \}_{i = 1}^n \overset{IID}{\sim} \{Z, Y(1), Y(0), X\},\] em que \(X_i \in \{1, \cdots, K\}\).
SRE (super população)
\[Z \perp\!\!\!\perp \{Y(1), Y(0) \} | X.\]
Então, \[\tau_{[k]} = \mathbb{E}(Y(1) - Y(0) | X = k) = \mathbb{E}(Y | Z = 1, X = k) - \mathbb{E}(Y | Z = 0, X = k).\]
Logo, \[\begin{align*} \tau & = \mathbb{E}(Y(1) - Y(0)) \\ & = \displaystyle \sum_{k = 1}^K p(X = k) \times \mathbb{E}(Y(1) - Y(0) | X = k) \\ & = \displaystyle \sum_{k = 1}^K p(X = k) \tau_{[k]} \\ \end{align*}\]
Carlos Trucíos (IMECC/UNICAMP) | ME920/MI628 - Inferência Causal | ctruciosm.github.io