Inferência Causal

Rerandomização e ajuste de regressão

Prof. Carlos Trucíos
ctrucios@unicamp.br

Instituto de Matemática, Estatística e Computação Científica (IMECC),
Universidade Estadual de Campinas (UNICAMP).

Introdução

Experimentos randomizados são o padrão ouro para estimar efeitos causais, porque a randomização equilibra, em média, todos os possíveis fatores de confusão (a.k.a. covariáveis). Contudo, pode acontecer que, em um determiado experimento, CRE crie grupos que são desbalanceados em alguma covariável importante.
Esse desbalanceamento traz consequências (já discutidas na aula anterior).
Nestes casos, continuamos com o experimento como esta ou re-randomizamos e continuamos o experimento com grupos balanceados?

Introdução

Estratificação e pós-estratificação são duais para covariável discreta no planejamento e análise de experimentos randomizados.
Mas como lidar com covariáveis multidimensionais e/ou contínuas?
Categorizar poderia ser uma respostas mas é longe de ser uma solução ótima 😿.
Rerandomizar e ajuste de regressão são o caminho a seguir 😄.

	Planejamento	Análise
Covariável Discreta	Estratificação	Pós-estratificação
Covariável Geral	Rerandomizar	Ajuste de regressão

Rerandomizar

Considere uma polulação com \(n\) unidades experimentais, das quais \(n_1\) recebem o tratamento e \(n_0\) o controle e seja \(\textbf{Z} = (Z_1, \cdots, Z_n)\) o vetor indicador de tratamento.
Para cada \(i\), seja \(X_i \in \mathbb{R}^K\) o vetor de covariáveis (discretas ou contínuas).
Denote, \(\textbf{X}_{n \times K} = (X_1, \cdots, X_n)'\) e por simplicidade assumiremos que \(n^{-1} \displaystyle \sum_{i = 1}^n X_i = 0.\)

Sob CRE, a diferença de médias das covariáveis, \[\hat{\tau}_X = n_1^{-1} \displaystyle \sum_{i = 1}^n Z_i X_i - n_0^{-1}\sum_{i = 1}^n (1- Z_i) X_i,\] tem \(\mathbb{E}(\hat{\tau}_X) = 0\) e \(\mathbb{V}(\hat{\tau}_X) = \dfrac{n}{n_1 n_0}S^2_X\), em que \(S^2_X = (n - 1)^{-1} \displaystyle \sum_{i = 1}^nX_i X_i'.\)

Rerandomizar

Randomizar, em média, equilibra as covariáveis.
Contudo, na alocação tratamento-controle realizada, é possível que covariáveis ainda sejam desbalanceadas, comprometendo a validade dos resultados.
Para evitar este desbalancemento, rerandomizamos.
Rerandomizar consite em refazer a randomização até que algum critério pre-especificado de equilibrio das covariáves seja atingido.
Este procedimento é computacionalmente caro (comparado com estratificar, por exemplo), mas hoje em dia isto não é mais um problema.

Rerandomizar

Uma forma de avaliar a diferença entre os grupos de tratamento e controle é através da distância de Mahalanobis:

\[M = \hat{\tau}_X' \Big (\underbrace{\dfrac{n}{n_1n_0}S^2_X}_{\mathbb{V}(\hat{\tau}_X)} \Big )^{-1}\hat{\tau}_X.\]

Lema

\(M\) permanece o mesmo se transformamos \(X_i\) em \(b_0 + B X_i\) para todas as unidades \(i = 1, \cdots, n\), em que \(b_0 \in \mathbb{R}^K\) e \(B \in \mathbb{R}^{K \times K}.\)

Sob CRE e para valores grandes de \(n\), \(M \sim \chi^2_K.\) Assim, \(M\) pode ter valores realizados grandes, afinal, \(M\) tem média \(K\) e variância \(2K\).

Rerandomizar

Code

mahalanobis2 = function(z, x) {
  x1 <- x[z == 1, ]
  x0 <- x[z == 0, ]
  n1 <- nrow(x1)
  n0 <- nrow(x0)
  diff <- apply(x1, 2, mean) - apply(x0, 2, mean)
  covar <- (n1 + n0)/(n1 * n0) * cov(x)
  M <- t(diff) %*% solve(covar) %*% diff
  return(M)
}

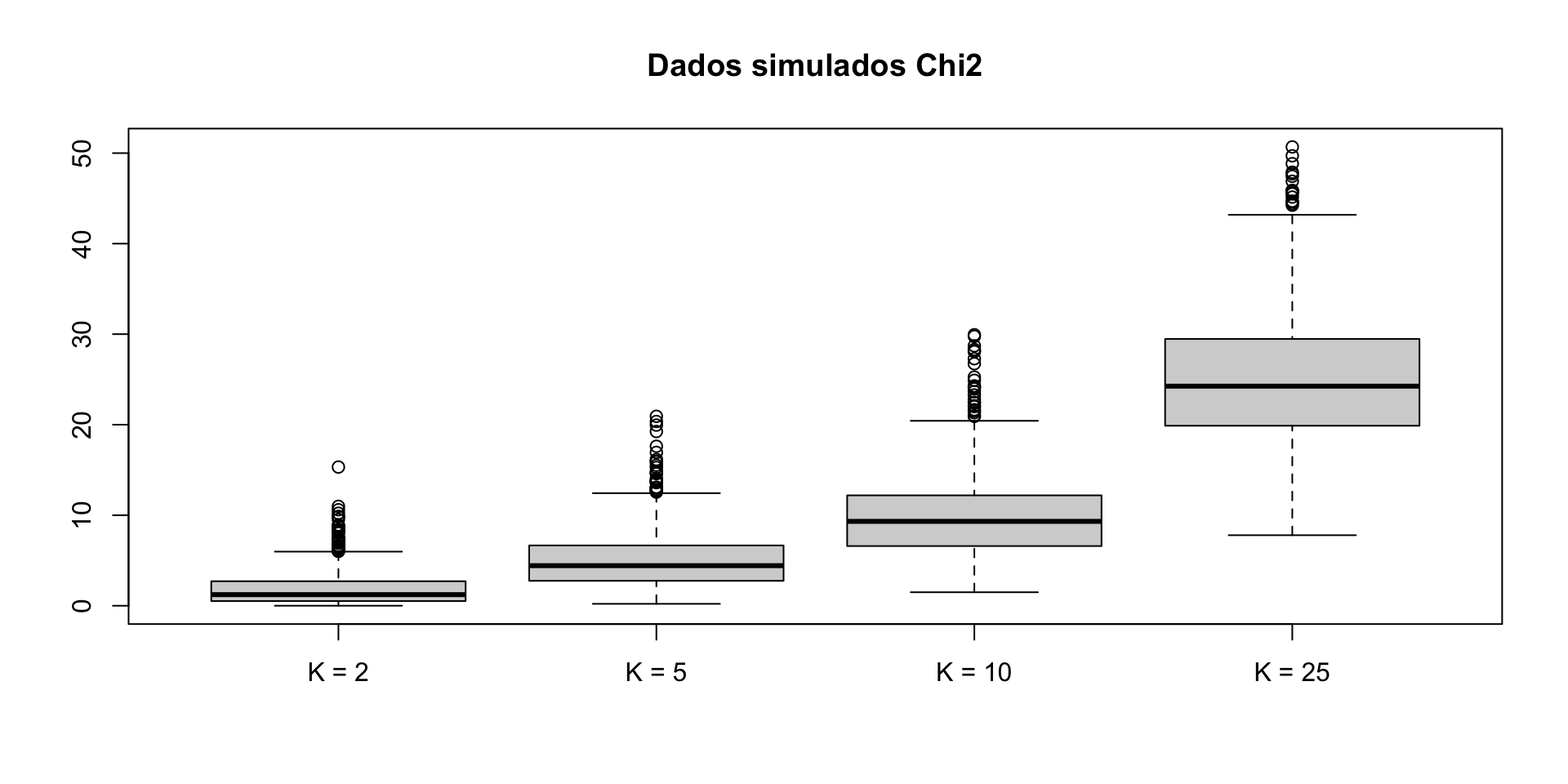
Rerandomizar

Rerandomizar evita o desbalanceamento das covariáveis descartando as alocações de tratamento (\(\textbf{z}\)) nas quais \(M\) é grande.

Definição (ReM): Rerandomizaçao utilizando a distância de Mahalanobis (\(M\))

Selecione \(\textbf{Z}\) de um CRE e aceite este sss \[M \leq a,\] para algum valor predeterminado de \(a > 0.\)

Como escolher a?

Uma prática comúm é escolher \(a\) pequeno ou utilizar algum quantil da \(\chi^2_K\).

Rerandomizar

Uma outra forma de escolher \(a\) é fixando primeiro \(p_a\) tal que \[p_a = P(M \leq a),\] em que \(p_a\) é a proporção de todas as randomizações consideradas aceitáveis pelo critério de rerandomização.
Na prática, a escolha de \(p_a\) é feita em termos do PRIV.

Percent Reduction in Variance (PRIV)

\[PRIV = 100 \times \Big (\dfrac{\mathbb{V}(\hat{\tau}_X) - \mathbb{V}_a(\hat{\tau}_X)}{\mathbb{V}(\hat{\tau}_X)} \Big) = 100 \times \Big ( 1 - \dfrac{P(\chi_{k+2}^2 \leq a)}{P(\chi_{k}^2 \leq a)} \Big)\]

Rerandomizar

Exemplo

Suponha que \(k = 10\), devemos escolher \(p_a = 0.001\) ou \(p_a = 0.0001\)?

\(p_a = 0.001 \rightarrow a = 1.478743 \rightarrow PRIV \approx 88\%\)
\(p_a = 0.0001 \rightarrow a = 0.8889204 \rightarrow PRIV \approx 93\%\)

Note que, o número de rerandomizações até o primeiro aceitável é \(1/p_a\). Dependendo do tempo computacional necessário (o que tem testes de permutação é um fator importante), o 5% adicional na redução da variância pode ou não valer a pena.

Rerandomizar

Code

rem <- function(x, n1, n0, a) {
  z     <- sample(c(rep(1, n1), rep(0, n0)))
  M     <- mahalanobis2(z, x)
  while (M > a) {
    z <- sample(z)
    M <- mahalanobis2(z, x)
  }
  return(z)
}

Rerandomizar

Como analisar dados sob ReM?

Sempre podemos utilizar FRT, desde que simulemos \(\textbf{Z}\) sob a restrição de que \(M \leq a\) (Morgan e Rubin, 2012).
Não temos propriedades em amostras finitas sem assumir a hipótese nula forte, mas temos alguns resultados assintóticos que nos ajudarão a testar a hipótese nula fraca.

Notação

Seja \(L_{K,a} \sim D_1 | \textbf{D}'\textbf{D} \leq a,\) em que \(\textbf{D} = (D_1, \cdots, D_K) \sim N_K(0, I)\) e seja \(\varepsilon \sim N(0,1)\), então \(L_{K, a}\) e \(\varepsilon\) são independentes

Rerandomizar

Teorema

Sob ReM com \(M \leq a\), quando \(n \rightarrow \infty\) e se as condições (1)–(3) acontecem, então \[\hat{\tau} - \tau \sim \sqrt{\mathbb{V}(\hat{\tau})} \Big \{\sqrt{R^2}L_{K,a} + \sqrt{1 - R^2}\varepsilon \Big \},\] em que \(\mathbb{V}(\hat{\tau}) = \dfrac{S^2(1)}{n_1} + \dfrac{S^2(0)}{n_0} - \dfrac{S^2(\tau)}{n}\) e \(R^2 = \mathbb{C}or^2(\hat{\tau}, \hat{\tau}_X)\) (sob CRE).

Condições:

\(n_1/n \rightarrow k_1\) e \(n_1/n \rightarrow k_2\) com \(0 \leq k_1, k_2 < \infty\).
\(\{X_i, Y_i(1), Y_i(0), \tau_i \}\) tem variância finita.
\(\max_{1 \leq i \leq n} \{Y_i(1)-\bar{Y}(1) \}^2 / n \rightarrow 0\), \(\max_{1 \leq i \leq n} \{Y_i(0)-\bar{Y}(0) \}^2 / n \rightarrow 0\) e \(\max_{1 \leq i \leq n} X_i'X_i / n \rightarrow 0\).

Quando \(a = \infty\), \(\hat{\tau}- \tau \sim \sqrt{\mathbb{V}(\hat{\tau})}\varepsilon\).
Quando \(a \rightarrow 0\), \(\hat{\tau}- \tau \sim \sqrt{\mathbb{V}(\hat{\tau})(1 - R^2)}\varepsilon\).

Rerandomizar

\[R^2 = \mathbb{C}or(\hat{\tau}, \hat{\tau}_X) = \dfrac{n_1^{-1}S^2(1|X) + n_0^{-1}S^2(0|X) - n^{-1}S^2(\tau | X)}{_1^{-1}S^2(1) + n_0^{-1}S^2(0) - n^{-1}S^2(\tau)},\] em que \(S^2(1)\), \(S^2(0)\), \(S^2(\tau)\) são as variâncias de \(\{Y_i(1)\}_{i = 1}^n\), \(\{Y_i(0)\}_{i = 1}^n\), \(\{\tau_i\}_{i = 1}^n\) e \(S^2(1|X)\), \(S^2(0|X)\), \(S^2(\tau|X)\) são as variâncias das suas projeções em \((1, X)\).

Quando \(0<a<\infty\), a distribuição de \(\hat{\tau}\) é bem mais complexa mas é mais concentrada em \(\tau\). Assim, \(\hat{\tau}\) é mais preciso sob ReM do que sob CRE.

Observação: Se ignorarmos o ReM e ainda utilizarmos o intervalo de confiança baseado na fórmula de variância de Neyman (1923) e na aproximação Normal, este será excessivamente conservador.

Ajuste de regressão

O que acontece se não fizemos uma rerandomização na etapa de planejamento mas queremos lidar com o desbalanceamento das covariáveis?

Obviamente não somos Marty McFly e não podemos voltar no tempo para utilizar rerandomização. Contudo, não todo está perdido e é aqui que ajuste de regressão entra no jogo.

Ajuste de regressão

FRT ajustado por covariável

As covariáveis \(\textbf{X}\) são todas fixas e, sob \(H_{0F}\), os resultados observados também são fixos. Assim, podemos simular a distribuição de qualquer test \(T = T(\textbf{Y}, \textbf{Z}, \textbf{X})\) e calcular p-valores. A ideia central do FRT continua a mesma na presença de covariáveis.

Existem duas estratégias gerais para construir a estatística de teste, as quais são apresentadas a seguir:

Ajuste de regressão

Definição: estratégia de pseudo-resultado

Podemos construir a estatística de teste baseados nos residuos (\(\hat{\varepsilon}\)) do modelo ajustado (considerando \(\textbf{Y}\) como variável dependente e \(\textbf{X}\) como independentes) e utilizar os resíduos como o pseudo-resultado para construir o teste.

Definição: estratégia da “saida” do modelo (model-output)

Podemos ajustar o modelo (considerando \(\textbf{Y}\) como variável dependente e \(\textbf{X}\) e \(\textbf{Z}\) como independentes) para obter o coeficiente de \(\textbf{Z}\) e utilizá-lo como estatística de teste.

Na primeira estratégia, precisamos rodar o modelo de regressão apenas uma vez. Já na segunda estratégia precisamos rodar o modelo várias vezes.

Observação: Um dos modelos ajustados mais utilizado é regressão linear (por MQO), mas nada impede que outras abordagens tais como regressão logística ou mesmo modelos de machine learning sejam utilizados.

Ajuste de regressão

E se não quisermos testar \(H_{0F}\) mas \(H_{0N}\)?

Os seguintes métodos focam na estimação do efeito médio causal, \(\tau\).

ANCOVA

Fisher (1925) propõe ANCOVA para melhorar a eficiência.
A ideia básica é ajustar um modelo de regressão por MQO, \[y_i = \beta_0 + \beta_1 z_i + \beta_2 x_{i1} + \cdots, \beta_{k+1} x_{ik} + u,\] e considerar \(\hat{\beta}_1\) como um estimador para \(\tau\), que será denotado aqui por \(\hat{\tau}_F\).

Ajuste de regressão

Freedman

David Freedman (2008) reanalisou ANCOVA sob o olhar dos resultados potenciais e encontrou o seguinte:

\(\hat{\tau}_F\) é viesado mas a simple diferença de médias, \(\hat{\tau}\), é não viesado.
A variância assintótica de \(\hat{\tau}_F\) pode ser ainda maior do que a de \(\hat{\tau}\) quando \(n_1 \neq n_0\).
O erro padrão do MQO é inconsistente para o verdadeiro erro padrão de \(\hat{\tau}_F\) sob CRE.

Lin

Winston Lin na sua tese de doutorado (2013), respondeu a algumas das críticas do Freedman e encontrou o seguinte:

O vies de \(\hat{\tau}_F\) é pequeno em grandes amostras e quando \(n \rightarrow \infty\), o vies \(\rightarrow 0\).
A eficiência assintótica de \(\hat{\tau}_F\) pode ser melhorada utilizando o coeficiente de \(Z_i\) resultante da regressão de \(\textbf{Y}\) sob \((1, \textbf{Z}, \textbf{X}, \textbf{Z} \times \textbf{X})\), denotaremos o estimador por \(\hat{\tau}_L\). Além disso, o erro padrão EHW é um estimador conservador do verdadeiro erro padrão de \(\hat{\tau}_L\) sob CRE.
O erro padrão EHW para \(\hat{\tau}_F\) ( regressão de \(\textbf{Y}\) sob \((1, \textbf{Z}, \textbf{X})\)) é um estimador conservador para o verdadeiro erro padrão de \(\hat{\tau}_F\)

Lin e SRE

Pode ser o caso de termos um SRE, estratificado numa variável discreta \(C\) e também termos outras covariáveis \(X\). Se todos os estratos são grandes, podemos obter um estimador de Lin como \[\hat{\tau}_{L,S} = \displaystyle \sum_{k = 1}^K \pi_{[k]} \hat{\tau}_{L,[k]},\] e um estimador (conservador) de \(\mathbb{V}(\hat{\tau}_{L,S})\) dado por \[\hat{V}_{L,S} = \displaystyle \sum_{k = 1}^K \pi_{[k]}^2 \hat{V}_{EHW, [k]}\]

Exemplo

[Angrist et al. (2009)]

Os dados vem de um experimento avaliando diferentes estratégias para melhorar o desempenho acadêmico nos calouros em uma universidade do Canada.
Por simplicidade, vamos focar apenas no grupo controle (control) e no tratamento que consiste em serviços de apoio acadêmico e incentivos financeiros (sfsp).
O resultado de interesse é o CR no final do primero ano (GPA_year1).
Dados faltantes são imputados com a média.
As covariáveis são genero (gender) e nota do vestibular (gpa0)
Os dados estão disponíveis aqui

Exemplo

[Angrist et al. (2009)]

Code

library(foreign)
library(dplyr)
library(car)
dados <- read.dta("datasets/star.dta")
dados <- dados |> 
  filter(control == 1 | sfsp == 1) |> 
  mutate(GPA_year1 = ifelse(is.na(GPA_year1), mean(GPA_year1, na.rm = TRUE), GPA_year1)) |> 
  select(GPA_year1, sfsp, female, gpa0)
y <- dados$GPA_year1
z <- dados$sfsp
x <- dados[, c("female", "gpa0")]

# Unadjusted estimator (Neyman)
modelo_unadj <- lm(y ~ z)
tau_unadj <- coef(modelo_unadj)[2]
se_unadj <- sqrt(hccm(modelo_unadj, type = "hc2")[2, 2])
c(tau_unadj, se_unadj)

         z            
0.05182942 0.07753077

Exemplo

[Angrist et al. (2009)]

Code

# Regression adjustment (Lin)
x <- scale(x)
modelo_adj <- lm(y ~ z*x)
tau_adj <- coef(modelo_adj)[2]
se_adj <- sqrt(hccm(modelo_adj, type = "hc2")[2, 2]) # apenas para manter coerencia com o ajuste anterior
c(tau_adj, se_adj)

        z           
0.0681657 0.0736601

Exemplo

[Angrist et al. (2009)]

Code

# Calculamo os p-valores
pvalor_unadj <- 2 - 2*pnorm(abs(tau_unadj/se_unadj))
pvalor_adj <- 2 - 2*pnorm(abs(tau_adj/se_adj))
c(pvalor_unadj, pvalor_adj)

        z         z 
0.5038137 0.3547533

Simulação

Code

library(ggplot2)
x2       <- cbind(x, x[, 2]^2)
dados_sim    <- data.frame(y = y, z = z, x2 = x2)
y1lm     <- lm(y ~ x2, weights = z, data = dados_sim)
sigma1   <- summary(y1lm)$sigma 
y0lm     <- lm(y ~ x2, weights = 1 - z, data = dados_sim)
sigma0   <- summary(y0lm)$sigma 

a  <- 0.05
mc <- 2000
n1 <- sum(z)
n0 <- sum(1 - z)
n <-  n1 + n0

rescale <- 0.2
y1_sim <- predict(y1lm, data = dados_sim) + rnorm(n)*sigma1*rescale
y0_sim <- predict(y0lm, data = dados_sim) + rnorm(n)*sigma0*rescale
tau <- mean(y1_sim - y0_sim)

tau_hat_cre <- rep(0, mc)
tau_hat_lim <- rep(0, mc)
tau_hat_rem <- rep(0, mc)
tau_hat_rem_lim <- rep(0, mc)

for (i in 1:mc) {
  ## CRE
  z_cre <- sample(z)
  y_cre <- z_cre * y1_sim + (1 - z_cre) * y0_sim
  tau_hat_cre[i] <- mean(y_cre[z_cre == 1]) - mean(y_cre[z_cre == 0])
  ## Regression Adjustement (Lim)
  tau_hat_lim[i] <- lm(y_cre ~ z_cre * x)$coef[2]
  ## ReM
  z_rem <- rem(x, n1, n0, a)
  y_rem <- z_rem * y1_sim + (1 - z_rem) * y0_sim
  tau_hat_rem[i] <- mean(y_rem[z_rem == 1]) - mean(y_rem[z_rem == 0])
  tau_hat_rem_lim[i] = lm(y_rem ~ z_rem * x)$coef[2]
}

Simulação

Code

data_plot <- data.frame(Est = c(tau_hat_cre, tau_hat_lim, tau_hat_rem, tau_hat_rem_lim),
                        Metodo = rep(c("CRE", "Lim", "ReM", "ReM-Lim"), each = mc))
ggplot(data_plot) + geom_boxplot(aes(x = Metodo, y = Est, fill = Metodo))

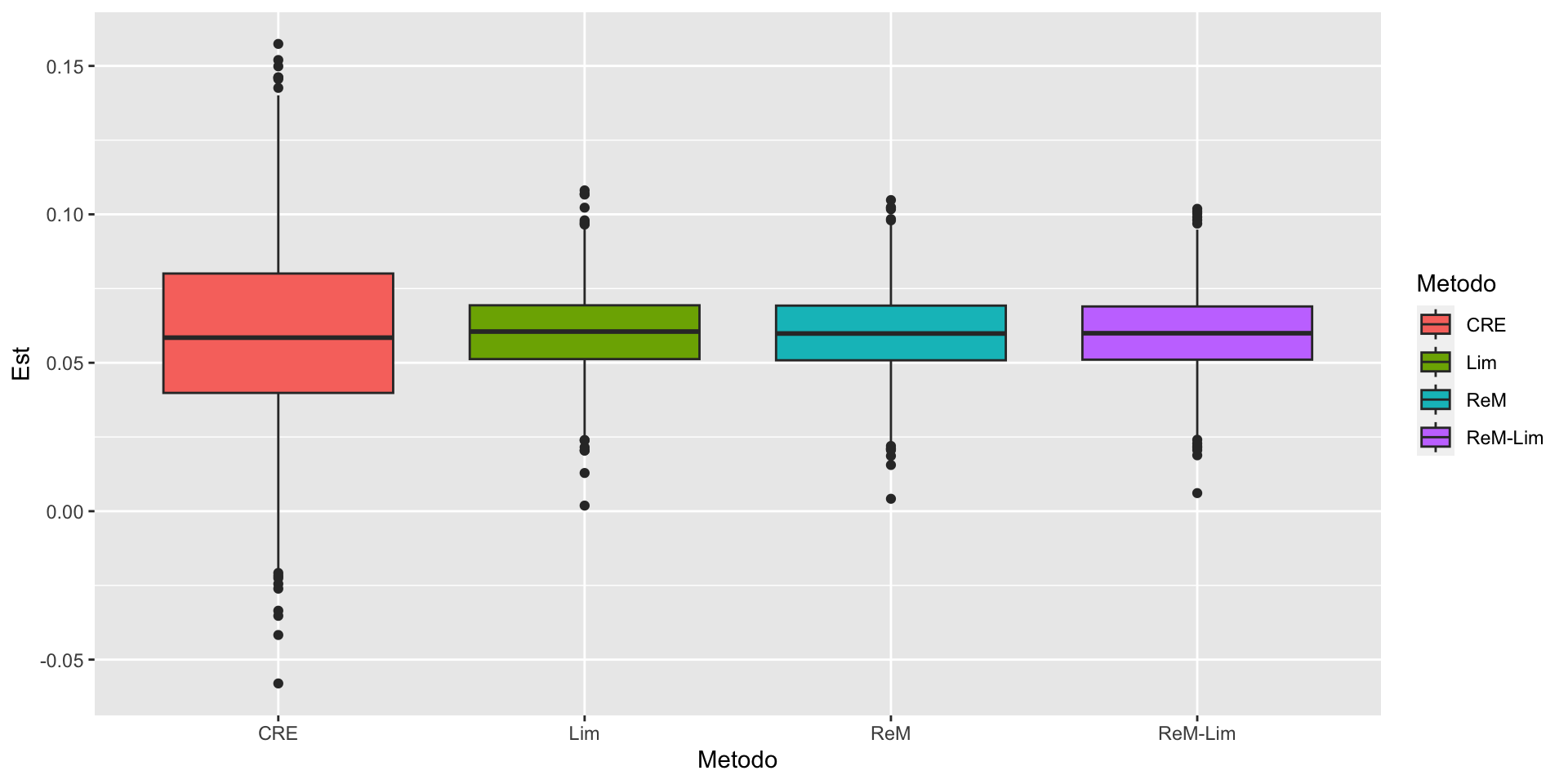
Simulação

Observação:

No experimento de simulação temos, além dos métodos vistos na aula de hoje, utilizado o estimador de Lim num contexto de rerandomização. De fato, Li e Ding (2020), mostram que é possível fazer isto e que, em geral, está combinação melhora o equilibrio da covariável tanto na parte do desenho amostral quando na parte de análise, dando uma maior eficiencia.

Code

c(sd(tau_hat_cre), sd(tau_hat_lim), sd(tau_hat_rem), sd(tau_hat_rem_lim))

[1] 0.03041661 0.01374499 0.01389687 0.01352262

Importante

Li et al. (2018) mostram quem, quando \(a\) é pequeno, a distribuição assintótica de \(\hat{\tau}\) sob ReM e a distribuição assintócica de \(\hat{\tau}_L\) sob CRE são quase idênticas.

Referências

Peng Ding (2023). A First Course in Causal Inference. Capítulo 6.
Morgan, K. L., & Rubin, D. B. (2012). Rerandomization to improve covariate balance in experiments.
Angrist, J., Lang, D., & Oreopoulos, P. (2009). Incentives and services for college achievement: Evidence from a randomized trial. American Economic Journal: Applied Economics, 1(1), 136-163.
Li, X., & Ding, P. (2020). Rerandomization and regression adjustment. Journal of the Royal Statistical Society Series B: Statistical Methodology, 82(1), 241-268.
Li, X., Ding, P., & Rubin, D. B. (2018). Asymptotic theory of rerandomization in treatment–control experiments. Proceedings of the National Academy of Sciences, 115(37), 9157-9162.