Risk-based Portfolio Allocation Strategies
ctrucios@unicamp.br
Instituto de Matemática, Estatística e Computação Científica (IMECC),
Universidade Estadual de Campinas (UNICAMP).
A statistician working on portfolio allocation?
A statistician working on portfolio allocation?

A statistician working on portfolio allocation?


A statistician working on portfolio allocation?

Introduction
Introdução

Introdução
- Suponha que temos 2 ativos, \(A\) e \(B\), nos quais estamos interessados em investir. Como alocaria seus recursos neste investimento?
- Suponha que temos 2 ativos, \(A\) e \(B\), com retornos esperados de \(3\) e \(5\) e variâncias iguais \(2\) e \(4\), respectivamente. Como alocaria seus recursos de forma a maximizar seu retorno esperado e minimizar seu risco?
- Suponha que temos 2 ativos, \(A\) e \(B\), com retornos esperados de \(3\) e \(5\) e variâncias iguais \(2\) e \(4\), respectivamente e correlação igual a 0.5. Como alocaria seus recursos de forma a maximizar seu retorno esperado e minimizar seu risco?
- Seja \(\omega\) e \(\mu\) os vetores (coluna) de pesos e retornos esperados, respectivamente e seja \(\Sigma\) a matriz de covariância associada (risco). Queremos maximizar \[\mu' \omega - \lambda \omega' \Sigma \omega,\] em que \(\lambda\) é o parâmetro de aversão ao risco (quanto maior, mais advessos ao risco somos)
Markowitz
Markowitz (1952)
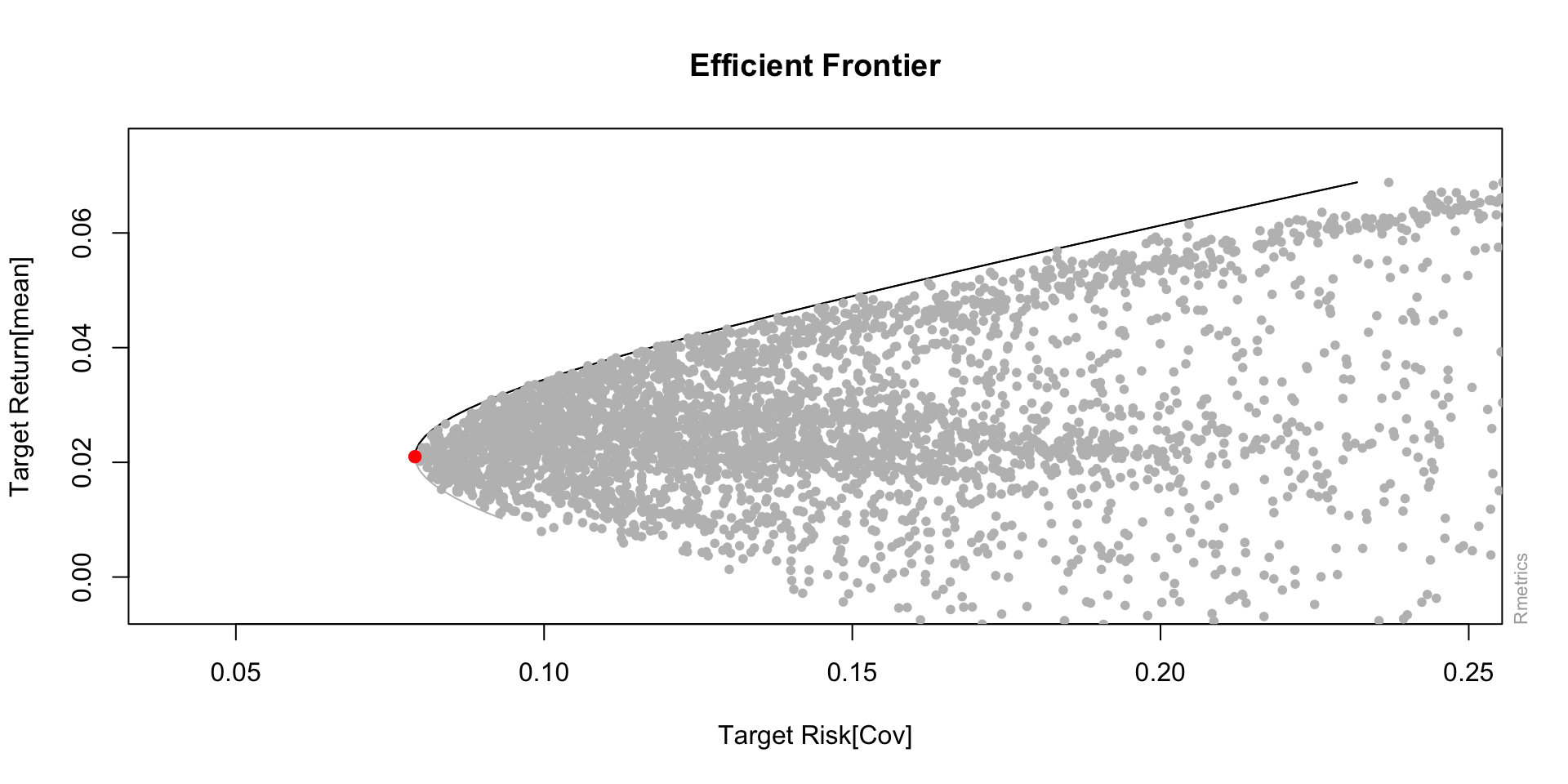
Markowitz
Quando \(\lambda\) é grande, o problema a ser resolvido, torna-se, aproximadamente, minimizar \[\omega' \Sigma \omega,\]
- Vamos assumir que todo nosso capital será alocado, ou seja \(\displaystyle \sum_{i = 1}^N\omega_i = 1\)
- Então, queremos minimizar com restrição
Markowitz
Seja um portfolio com \(N\) ativos e matriz de covariância \(\Sigma\). Queremos minimizar \[L(\boldsymbol{\omega}, \lambda) = \boldsymbol{\omega}' \Sigma \boldsymbol{\omega} + \lambda (\boldsymbol{1}'\boldsymbol{\omega} - 1),\] em que \(\boldsymbol{1} = [1, 1, \cdots, 1]'.\)
Derivando w.r.t. \(\boldsymbol{\omega}\) e \(\lambda\)
- \(\dfrac{\partial L}{\partial \boldsymbol{\omega}} = 2 \Sigma \boldsymbol{\omega} + \lambda \boldsymbol{1}\)
- \(\dfrac{\partial L}{\partial \lambda} = \boldsymbol{1}' \boldsymbol{\omega} - 1\)
Igualando a zero, \[\Sigma \boldsymbol{\omega} = - \dfrac{\lambda \boldsymbol{1}}{2} \rightarrow \boldsymbol{\omega} = \dfrac{-\lambda}{2} \Sigma^{-1} \boldsymbol{1}\]
Markowitz
Igualando a zero \(\dfrac{\partial L}{\partial \lambda} = \boldsymbol{1}' \boldsymbol{\omega} - 1\), temos:
\[1 = \boldsymbol{1}' \boldsymbol{\omega} = \dfrac{-\lambda}{2} \boldsymbol{1}' \Sigma^{-1} \boldsymbol{1} \rightarrow \lambda = \dfrac{-2}{\boldsymbol{1}' \Sigma^{-1} \boldsymbol{1}}.\]
Assim,
\[\boldsymbol{\omega} = \dfrac{-\lambda}{2} \Sigma^{-1} \boldsymbol{1} = \dfrac{\Sigma^{-1} \boldsymbol{1}}{\boldsymbol{1}' \Sigma^{-1} \boldsymbol{1}},\] são os pesos ótimos da carteira de variância mínima.
Hands-On I
Hands-On I
Utilizando retornos mensais das ações na B3, calcularemos os pesos para a carteira de variância mínima. Utilizaremos os pacotes do R yfR, RiskPortfolios, tidyr e dplyr.
Hands-On I
Hands-On
Code
Hands-On
Code
[,1]
ASSET1 0.1450
ASSET2 0.2530
ASSET3 0.2270
ASSET4 0.1988
ASSET5 0.1868
ASSET6 -0.0297
ASSET7 0.0578
ASSET8 0.0150
ASSET9 -0.0505
ASSET10 -0.0033\[\boldsymbol{\omega} = \dfrac{\Sigma^{-1} \boldsymbol{1}}{\boldsymbol{1}' \Sigma^{-1} \boldsymbol{1}},\]
Hands-On
Code
omega
ASSET1 0.14497249 0.14497249
ASSET2 0.25304038 0.25304038
ASSET3 0.22699176 0.22699176
ASSET4 0.19881419 0.19881419
ASSET5 0.18675677 0.18675677
ASSET6 -0.02965077 -0.02965077
ASSET7 0.05782148 0.05782148
ASSET8 0.01501568 0.01501568
ASSET9 -0.05046142 -0.05046142
ASSET10 -0.00330055 -0.00330055Hands-On I
- Na prática, \(\Sigma\) não é conhecido, devendo ser estimado com os dados (\(\hat{\Sigma}\)).
- Utilizar \(\hat{\Sigma}\) em lugar de \(\Sigma\) implica em erro de estimação.
- Isto faz com que os pesos estejam alocados em poucos ativos, exista pouca diversificação e o desempenhho fora da amostra seja pobre 😢
- Para lidar com este problema, diversas abordagens tem sido propostas.
Observações:
- Na prática é muito dificil estimar \(\mu\). É por isso que carteiras baseadas em rico (\(\Sigma\)) são preferidas.
- É comúm impor a restrição de que \(\omega_i \geq 0\) (no-short-selling constraints ou restrição de não venda a descoberto).
Hands-On I
Outros portfolios
Outros portfolios
Pesos iguais
- Também chamada de estratégia ingênua ou \(1/N\).
- É a estratégia mais simples e não precisa cálculos difíceis nem resolver problemas de otimização.
- Para um conjunto de \(N\) ativos financeiros, os pesos são obtidos como \[\omega_i = 1/N, \quad \forall i= 1, \cdots, N.\]
- Apesar da sua simplicidade, diversos autores mencionam que o desempenho fora da amostra desta estratégia é dificilmente superado por métodos mais complexos (DeMiguel et al. 2009)
Outros portfolios
Volatilidade inversa
Proposto por Leote De Carvalho et al. (2012), esta estratégia não leva em consideração covariâncias, mas apenas variâncias. Os pesos são obtidos como:
\[\boldsymbol{\omega} = \Big( \dfrac{1/\sigma_1}{ \displaystyle \sum_{j = 1}^N 1/\sigma_j}, \cdots, \dfrac{1/\sigma_N}{ \displaystyle \sum_{j = 1}^N 1/\sigma_j} \Big)'\]
No R
optimalPortfolio(Sigma, control = list(type = 'invvol', constraint = 'lo'))
Outros portfolios
Diversificação máxima
Proposto por Choueifaty and Coignard (2008), o objetivo é maximizar a razão \[DR = \dfrac{\boldsymbol{\omega}'\boldsymbol{\sigma}}{\sqrt{\boldsymbol{\omega}' \Sigma \boldsymbol{\omega}}},\] sujeito á restrição de que \(\boldsymbol{1}' \boldsymbol{\omega} = 1\) e \(\omega_i \geq 0\) e em que \(\boldsymbol{\sigma} = \sqrt{diag(\Sigma)}\).
Note que no caso extremos de que a carteira esteja formada po apenas um ativo, \(DR = 1\), implicando uma carteira pobremente diversificada.
No R
optimalPortfolio(Sigma, control = list(type = 'maxdiv', constraint = 'lo'))
Outros portfolios
Igual contribuição ao risco
Popularizada por Qian (2005), a ideia desta estratégia é que cada um dos ativos tenha a mesma contribuição marginal ao risco (volatilidade) da carteira, ou seja, que a proporção da contribuição ao risco de cada ativo deve ser \(1/N\). Ativos com pouco risco receberão pessos maiores e ativos com muito risco receberão pesos menores.
Os pesos são obtidos minimizando \[\displaystyle \sum_{i = 1}^N (\%RC_i - 1/N)^2,\] sujeito á restrição de que \(\boldsymbol{1}' \boldsymbol{\omega} = 1\), em que \(\%RC_i = \omega_i [\Sigma \boldsymbol{\omega}]_i / \boldsymbol{\omega}' \Sigma \boldsymbol{\omega}\) é a porcentagem de risco com que o ativo \(i\) contribui para o risco total.
No R
optimalPortfolio(Sigma, control = list(type = 'erc', constraint = 'lo'))
Outros portfolios
Máxima decorrelation
Proposto por Christoffersen et al. (2012), esta estratégia pode ser vista como um caso particular do portfolio de variância mínima mas com \(\rho\) (matriz de correlação) em lugar de \(\Sigma\) (matriz de covariância). Assim, queremos minimizar \[\boldsymbol{\omega} \rho \boldsymbol{\omega},\] sujeito á restrição de que \(\boldsymbol{1}' \boldsymbol{\omega} = 1\)
No R
optimalPortfolio(Sigma, control = list(type = 'maxdec', constraint = 'lo'))
Hands-On II
Hands-On II
Utilizando os dados anteriores, calcularemos os pesos ótimos utiliando as estratégias vistas anteriormente.
Code
omega_invol <- optimalPortfolio(Sigma, control = list(type = 'invvol', constraint = 'lo'))
omega_erc <- optimalPortfolio(Sigma, control = list(type = 'erc', constraint = 'lo'))
omega_maxdiv <- optimalPortfolio(Sigma, control = list(type = 'maxdiv', constraint = 'lo'))
omega_maxdec <- optimalPortfolio(Sigma, control = list(type = 'maxdec', constraint = 'lo'))Hands-On II
Code
MV IV ERC MaxDiv MaxDec
ASSET1 0.14441636 0.10180771 0.10302562 0.04982798 0.04891108
ASSET2 0.19927819 0.10138439 0.08394694 0.03722635 0.03669391
ASSET3 0.19731862 0.10180305 0.10214902 0.12238143 0.12013496
ASSET4 0.19871602 0.10124235 0.14352016 0.19926099 0.19668659
ASSET5 0.18682494 0.10154481 0.10313840 0.07846716 0.07722268
ASSET6 0.00000000 0.09871593 0.09834150 0.07444889 0.07536776
ASSET7 0.05856234 0.09900181 0.10191129 0.15308962 0.15453158
ASSET8 0.01488354 0.09823150 0.10044598 0.12267356 0.12480008
ASSET9 0.00000000 0.09820804 0.08129069 0.05246468 0.05338689
ASSET10 0.00000000 0.09806042 0.08223041 0.11015936 0.11226446ML Risk-Based Portfolios
ML Risk-Based Portfolios
- Recentemente, novas estratégias de alocação de carteiras baseadas em machine learning tem surgido na literatura.
- Algumas destas estratégias utilizam algoritmos de clusterização hierárquica (HRP, HCAA, HERC, DHRP).
- Estas estratégias surgem para superar algumas das limitações da estratégia de Markowitz, bem como incluir a ideia de que “sistemas complexos, como o mercado financeiro, estão organizados de forma hierárquica”
ML Risk-Based Portfolios
Hierarchical Risk Parity (HRP)
- Proposta por Lopez de Prado (2016)
- Surge como uma alternativa para evitar os problemas observados da optimização de Markowitz.
- A ideia básica do algoritmo é transformar a matriz de covariância em matriz de distâncias, aplicar um método de agrupamento hierárquico, fazer bissecções e calcular os pesos através da estratégia de volatilidade inversa.
ML Risk-Based Portfolios
Hierarchical Risk Parity (HRP)
- A matriz de distância utilizada no método de agrupamento hierárquico é denotada por \(\tilde{D}\) cujos elementos \({\tilde{d}_{ij}}\) são obtidos como \[\tilde{d}_{ij} = \sqrt{\displaystyle \sum_{k = 1}^N (d_{ki} - d_{kj})^2},\] em que \(N\) é o número de ativos e \(d_{ij} = \sqrt{0.5 \times (1 - \rho_{ij})}\) com \(\rho_{ij}\) sendo a correlaçõ entre os ativos \(i\) e \(j\).
ML Risk-Based Portfolios
Hierarchical Risk Parity (HRP)

ML Risk-Based Portfolios
Hierarchical Risk Parity (HRP)
- Inicialize todos os pesos em \(\omega_i = 1\)
- Dentro de cada grupo, o vetor de pesos prévios do grupo \(k\) (\(k = 1, 2\)) é obtido através do método de volatilidade inversa, \[\boldsymbol{\omega}_{aux}^{(k)} = \dfrac{1}{Trace(Diag(\Sigma^{(k)})^{-1})} \times Diag(\Sigma^{(k)})^{-1},\] em que \(\Sigma^{(k)}\) é a matriz de covariância dos ativos no grupo \(k\).
- Com os pesos obtidos, calculamos a variância de cada grupo como \(V^{(k)} = \boldsymbol{\omega}_{aux}^{(k)} \Sigma^{(k)}\boldsymbol{\omega}_{aux}^{(k) \prime},\) e, finalmente \(\alpha = 1 - \frac{V^{(1)}}{V^{(1)} + V^{(2)}}\) que é um fator de ponderação que atualizará o peso de cada ativo.
- Os pesos finais são atualizados para \(\boldsymbol{\omega}^{(1)} = \alpha \boldsymbol{\omega}^{(1)}\) e \(\boldsymbol{\omega}^{(2)} = (1 - \alpha) \boldsymbol{\omega}^{(2)}\).
- O processo se repete até que cada grupo tenha apenas um ativo.
ML Risk-Based Portfolios
Hierarchical Risk Parity (HRP)

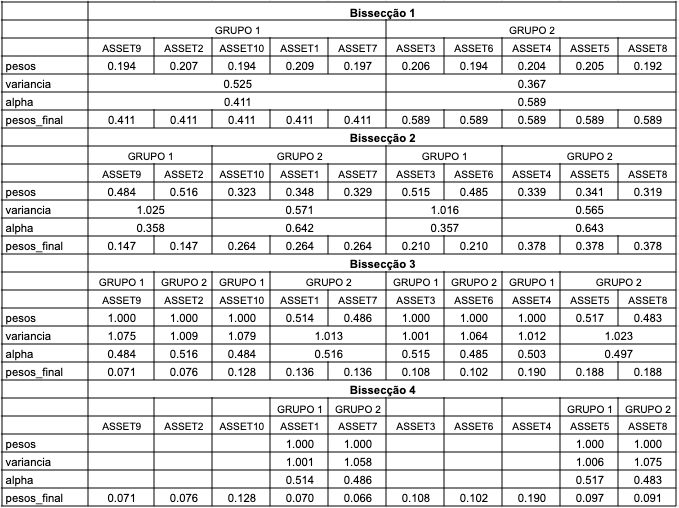
ML Risk-Based Portfolios
Hierarchical Risk Parity (HRP)
ML Risk-Based Portfolios
Hierarchical Risk Parity (HRP)
- Uma das críticas do HRP é que ele não utiliza a clusterização mas apenas a ordem.
- Algumas modificações do algoritmo surguiram na literatura:
- Hierarchical Clustering-Based Asset Allocation (HCAA) (Raffinot, 2017)
- Hierarchical Equal Risk Contribution (HERC) (Raffinot, 2018)
- A Constrained Hierarchical Risk Parity Algorithm with Cluster-based Capital Allocation (DHRP) (Pfitzingera and Katzke, 2019)
ML Risk-Based Portfolios
A Constrained Hierarchical Risk Parity Algorithm with Cluster-based Capital Allocation (DHRP)
- Visando incorporar uma maior parte da informação extraida a partir da clusterização, bem como incluir algumas práticas usuais do mercado financeiro, Pfitzinger et al.(2019) propõe três modificações à proposta de Lopez de Prado (2016).
- A primeira modificação consiste em utilizar um algoritmo divisivo em vez de algoritmo aglomerativo como sugerido por Lopez de Prado (2016).
- Permite a inclusão de restrições nos pesos e,
- Através de um parâmetro \(\tau\), é possível aproveitar toda a estrutura hierarquica obtida na clusterização (\(\tau = 1\)), parte dela (\(\tau \in (0, 1)\)) ou apenas a ordenação (\(\tau = 0\)).
ML Risk-Based Portfolios
Hierarchical Clustering-Based Asset Allocation (HCAA)
- HRP e DHRP não levam em consideração o número de clusters a serem formados.
- HCAA leva isto em consideração e, após selecionar o número de grupos a serem formados, os pesos são calculados entre os grupos e dentro dos grupos.
- A ideia é distribuir o capital total a ser investido de forma igual entre os clusters hierarquicamente (assim ativos correlacionados que formarão um cluster recebem o mesmo peso total do que um ativo não correlacionado, obtendo diversificação).
- Dentro de cada cluster, os pesos são calculados através da estratégia de pesos iguais.
ML Risk-Based Portfolios
Hierarchical Clustering-Based Asset Allocation (HCAA)
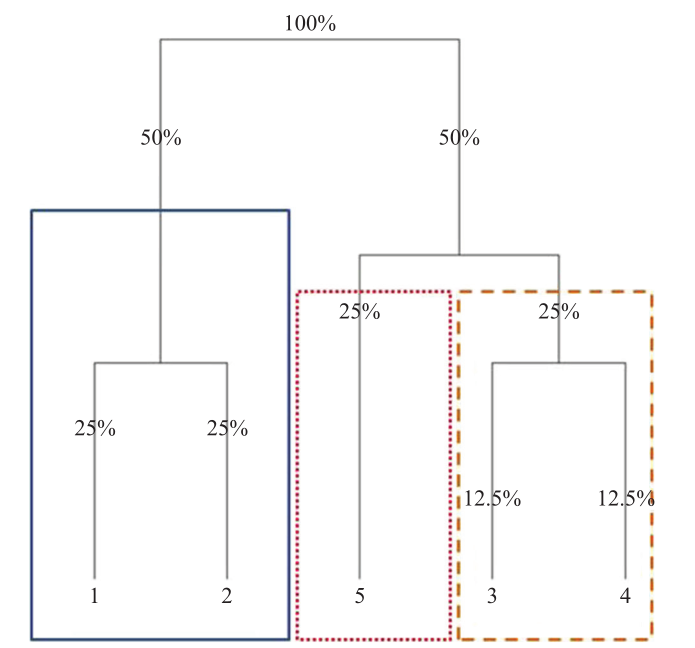
ML Risk-Based Portfolios
Hierarchical Clustering-Based Asset Allocation (HCAA)
ML Risk-Based Portfolios
Hierarchical Equal Risk Contribution (HERC)
- HRP faz as bissecções considerando apenas a ordem do dendrograma e não o dendrograma per se.
- Parecido com HACC mas em lugar de calcular os pesos de forma que o total a ser investido seja dividio de forma igual entre cluster, calcula os pesos de forma que a contribuição ao risco seja a mesma dentro de cada cluter.
- Dentro de cada cluster, utiliza-se o método de volatilidade inversa.
ML Risk-Based Portfolios
Hierarchical Equal Risk Contribution (HERC)
ML Risk-Based Portfolios
Hierarchical Equal Risk Contribution (HERC)
- Fazer um agrupamento hierárquico. Raffinot 2018 sugere utilizar a ligação ward mas qualquer outra ligação poderia ser utilizada.
- Selecionar o número de clusters a serem utilizados segundo algum critério. Raffinot 2018 sugere utilizar o índice Gap.
- Dentro de cada cluster, calcular os pesos (iniciais) segundo o método Naive Risk Parity.
- Utilizando os pesos obtidos no paso anterior, calcular o risco de cada cluster (e em cada hierarquia).
- Em cada hierarquia, calcular os pesos como \(\omega^{(1)} = \dfrac{RC_2}{RC_1 + RC_2}\) e \(\omega^{(2)} = \dfrac{RC_1}{RC_1 + RC_2}\), em que RC é o risco no cluster. Por ultimo, os pesos iniciais serão atualizados utilizando os diveros \(\omega^{(1)}\) e \(\omega^{(2)}\) obtidos.
ML Risk-Based Portfolios
Hierarchical Equal Risk Contribution (HERC)
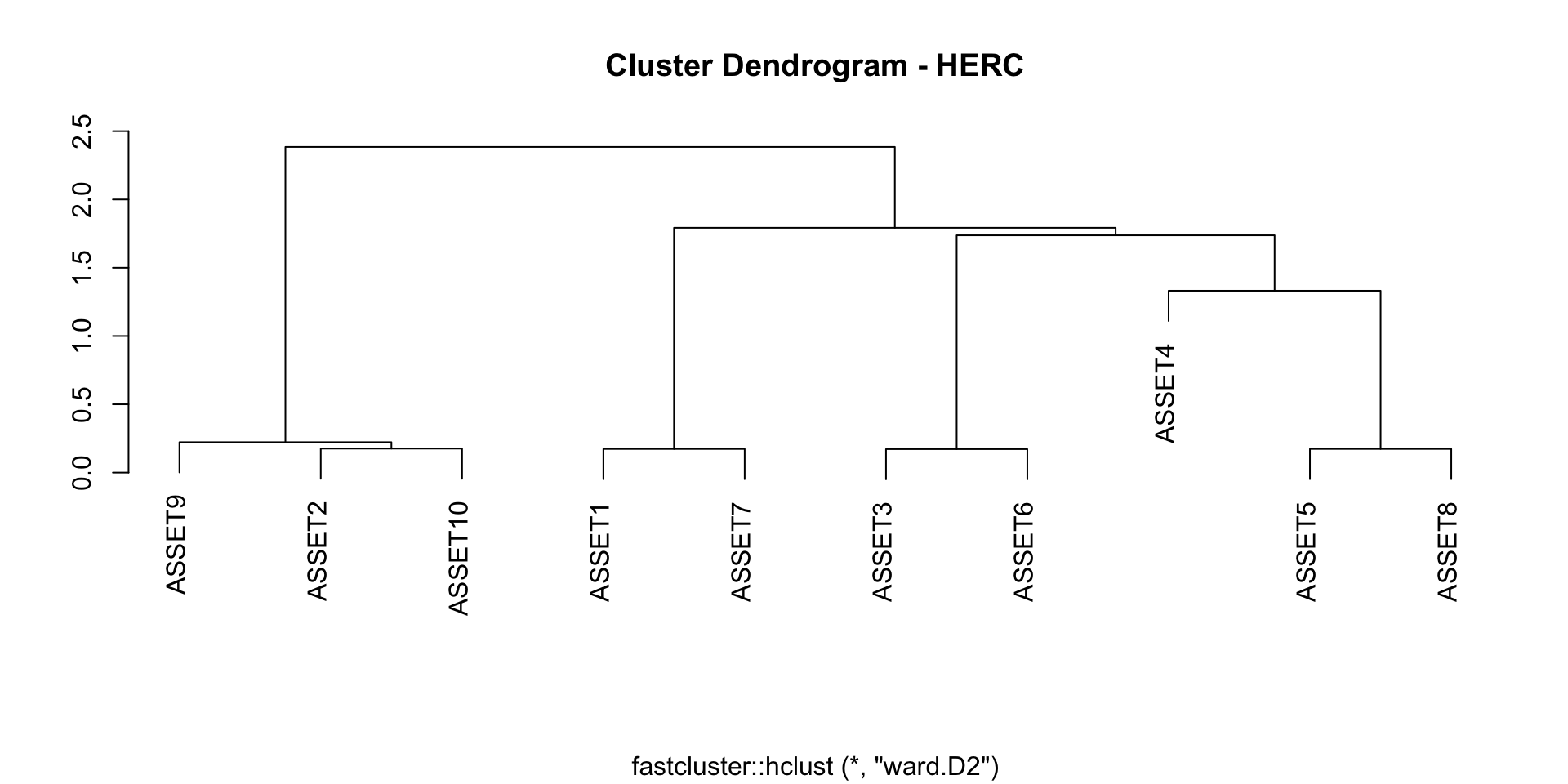
ML Risk-Based Portfolios
Code
MV IV MaxDec MaxDiv ERC HRP DHRP HACC HERC
ASSET1 0.144 0.102 0.049 0.050 0.103 0.070 0.109 0.125 0.078
ASSET2 0.199 0.101 0.037 0.037 0.084 0.076 0.053 0.167 0.278
ASSET3 0.197 0.102 0.120 0.122 0.102 0.108 0.104 0.062 0.017
ASSET4 0.199 0.101 0.197 0.199 0.144 0.190 0.194 0.062 0.008
ASSET5 0.187 0.102 0.077 0.078 0.103 0.097 0.099 0.031 0.004
ASSET6 0.000 0.099 0.075 0.074 0.098 0.102 0.098 0.062 0.016
ASSET7 0.059 0.099 0.155 0.153 0.102 0.066 0.103 0.125 0.074
ASSET8 0.015 0.098 0.125 0.123 0.100 0.091 0.093 0.031 0.004
ASSET9 0.000 0.098 0.053 0.052 0.081 0.071 0.098 0.167 0.261
ASSET10 0.000 0.098 0.112 0.110 0.082 0.128 0.049 0.167 0.260Avaliando Portfolios
Medidas de desempenho
Seja \(p\) o tamanho do período fora da amostra
- Average (AV): \[AV = 12\frac{\sum_{i = 1}^{p}R_{i}}{p},\] em que \(R_{i}\) são os retornos fora da amostra. AV calcula a média anualizado o qual é multiplicado por 12. Quanto maior, melhor o desempenho da carteira.
- Standard Deviation (SD): \[SD = \sqrt{12}\hat{\sigma}_{p},\] em que \(\hat{\sigma}_{p}\) é o desvio-padrão anualizado dos retornos fora da amostra. Quanto menor, menor o risco e tem um desempenho melhor da carteira.
Medidas de desempenho
- Sharpe Ratio (SR): \[SR = \frac{\bar{R}_{p} - \bar{R}_{f}}{\bar{\sigma}_{p-f}},\] em que \(R_{f}\) é a taxa livre de risco, \(\bar{R}_{p}\) é a média dos retornos fora da amostra e \(\bar{\sigma}_{p-f}\) é desvio-padrão estimado do excesso de retorno. Quanto maior, melhor o desempenho da carteira.
- Adjusted Sharpe Ratio (ASR): \[SR = SR(1 + (\frac{\mu_{3}}{6})SR - (\frac{\mu_{4}-3}{24})SR^2),\] em que \(\mu_{3}\) é a assimetria, \(\mu_{4}\) é a cúrtose e \(SR\) é o Sharpe Ratio acima apresentado. Está métrica ajusta o Sharpe ratio incluindo o terceiro e segundo momento amostral. Quanto maior este valor, melhor o desempenho da carteira.
Medidas de desempenho
- Sortino ratio (SO): \[SO = \frac{\bar{R}_{p}}{\sqrt{\frac{\sum_{i=1}^{K}min(0,R_{p,i} - MAR)^2}{K}}},\] em que \(K\) é o tamanho do periodo fora da amostra e MAR é retorno mínimo aceitado, os quais é igual a taxa livre de risco mensal. Quanto maior, melhor o desempenho de portfólio.
Aplicação
Aplicação
Code
Error in dplyr::rename(., ticker = Ticker, company = Company, industry = Industry) :
Can't rename columns that don't exist.
✖ Column `Ticker` doesn't exist.Code
ibov_tickers <- paste0(acoes$ticker, ".SA")
retornos <- yf_get(tickers = ibov_tickers,
first_date = "2010-01-01",
last_date = "2024-04-30",
freq_data = "monthly") |>
select(ref_date, ticker, ret_adjusted_prices) |>
pivot_wider(id_cols = ref_date, values_from = ret_adjusted_prices, names_from = ticker) |>
drop_na()
retornos[, -1] <- retornos[, -1]*100
glimpse(retornos)Rows: 145
Columns: 64
$ ref_date <date> 2012-04-02, 2012-05-02, 2012-06-01, 2012-07-02, 2012-08-01,…
$ ABEV3.SA <dbl> 7.11404489, -7.15027039, 1.25521655, 1.80493276, -0.82423748…
$ ALPA4.SA <dbl> 7.979721, -17.395751, 5.098031, -9.104464, 8.119680, 8.69563…
$ AMER3.SA <dbl> -2.0481893, -25.4612612, -3.4653487, 14.1880461, 17.5149651,…
$ B3SA3.SA <dbl> -4.6263164, -9.8467027, 7.3298642, 12.1950528, -6.0574288, 1…
$ BBAS3.SA <dbl> -9.1329184, -14.9411726, -0.9076693, 11.6230722, 6.8994761, …
$ BBDC3.SA <dbl> -5.1420765, -3.6453849, 0.9580030, 5.6350921, 3.4586492, -1.…
$ BBDC4.SA <dbl> -3.8981990, -3.3072231, 1.9174968, 5.6063285, 4.0235991, -0.…
$ BEEF3.SA <dbl> 22.2065440, -10.4166955, 9.5607187, 8.6084945, 15.3094618, 5…
$ BPAN4.SA <dbl> -9.9560501, -24.3902491, 9.6774017, -22.5490137, 22.7848004,…
$ BRAP4.SA <dbl> 4.0093897, -9.5701796, 4.3726261, -6.7092002, -14.3832978, 6…
$ BRFS3.SA <dbl> -3.1944294, -9.9282766, -2.8186487, -3.4550866, 11.1451994, …
$ BRKM5.SA <dbl> -3.1329618, -16.0447706, 18.9333512, -7.3991204, 3.3091284, …
$ CCRO3.SA <dbl> 0.5160133, 6.0810779, 4.0127475, 4.7152526, 6.6666755, -2.35…
$ CMIG4.SA <dbl> 10.4559178, -6.8819791, 6.6341774, 4.3962597, -11.7661665, -…
$ COGN3.SA <dbl> 0.0000000, 0.0000000, -32.3077009, -9.0909151, 10.0000073, 0…
$ CPFE3.SA <dbl> 0.01621584, -7.39211285, 2.91733701, -6.92914586, -5.8695342…
$ CPLE6.SA <dbl> 14.773955, -15.054880, 7.752282, -4.796352, -14.211029, -8.3…
$ CSAN3.SA <dbl> -2.5323981, -9.4864230, 3.4379528, 0.6776224, 10.8042393, 9.…
$ CSNA3.SA <dbl> -0.2124576, -20.5504500, -12.3941774, -7.4692486, -5.6030157…
$ CYRE3.SA <dbl> -2.8672052, -1.8181497, -2.1164020, 0.0000000, 11.5540384, 5…
$ DXCO3.SA <dbl> -2.693320, -13.749999, 10.041404, 13.360964, 1.924685, 9.113…
$ ECOR3.SA <dbl> -0.3134660, 1.5094219, 0.1858710, 2.5974208, 0.9644228, 5.37…
$ EGIE3.SA <dbl> 1.6138506, 1.8265068, 11.0612363, -1.6150594, -4.8794278, -5…
$ ELET3.SA <dbl> -4.9008186, -18.5889558, 7.3850620, -0.7017479, -7.9858739, …
$ ELET6.SA <dbl> -3.374089, -11.122027, 4.385041, 2.715151, -7.980051, -1.192…
$ EMBR3.SA <dbl> 12.2950973, -12.7128793, -6.3487057, -1.6467131, 6.5449076, …
$ ENEV3.SA <dbl> 8.2206293, -14.6748027, -11.1111101, 7.4675353, 14.1993969, …
$ ENGI11.SA <dbl> -0.4650800, 0.0000000, 0.4672531, -4.6511904, 4.3129832, 6.2…
$ EQTL3.SA <dbl> 2.7007203, 4.4776029, 2.0408541, 1.0666477, 2.5725544, 15.11…
$ EZTC3.SA <dbl> -4.1085802, -4.9881677, 3.1000153, 5.6256111, 12.7180946, 2.…
$ FLRY3.SA <dbl> 1.9087193, -1.7100794, 5.6337791, -16.0392348, 3.5926644, 9.…
$ GGBR4.SA <dbl> 2.6346012, -11.1746864, 11.6015531, 5.1977228, -3.1960870, 7…
$ GOAU4.SA <dbl> 3.37927438, -13.87172438, 10.97742525, 5.32972625, -4.602824…
$ GOLL4.SA <dbl> -16.7350290, -20.7881747, 10.9452751, 7.0627815, 1.5706766, …
$ HYPE3.SA <dbl> -4.8248880, -9.8119419, 7.6155645, 8.6773522, 1.9379790, 13.…
$ ITSA4.SA <dbl> -11.2803817, -2.7594441, -3.3541936, 13.0588685, -2.7055245,…
$ ITUB4.SA <dbl> -14.0770277, -2.2844785, -3.3975812, 14.8364329, -1.4783404,…
$ JBSS3.SA <dbl> 0.000000, -27.333337, 10.642198, -11.111110, 8.955231, 15.06…
$ JHSF3.SA <dbl> -0.1669474, 0.1672266, 0.1669474, 2.5000368, 28.1300602, -3.…
$ LREN3.SA <dbl> 0.34189458, -5.09219500, -2.79818482, 8.73115360, 9.22142011…
$ MGLU3.SA <dbl> -4.8494923, -17.9068265, 0.7502554, 9.0425186, 10.2438995, 8…
$ MRFG3.SA <dbl> -8.7826092, -13.2507266, 2.6373660, 1.1777355, 21.2698320, 2…
$ MRVE3.SA <dbl> -14.3629470, -18.4640387, 7.3903151, 19.8924439, 4.3049439, …
$ MULT3.SA <dbl> 5.50995962, 7.09807752, 2.63047858, 5.41089829, -0.01930367,…
$ PCAR3.SA <dbl> 3.4828470, 0.0000000, 0.9096970, 0.0000000, 0.9097256, 0.000…
$ PETR3.SA <dbl> -7.8600740, -10.6916624, -4.5454710, 6.0846615, 6.2344271, 9…
$ PETR4.SA <dbl> -8.8222474, -9.2159259, -4.6001375, 6.8493476, 6.4615223, 7.…
$ PRIO3.SA <dbl> -13.326792, -38.412409, -7.259255, -20.447291, -6.626503, -4…
$ QUAL3.SA <dbl> 6.0702898, 3.6144655, 2.0930185, 3.9293733, 9.3150904, -0.75…
$ RADL3.SA <dbl> 15.7183309, -9.2015837, 8.8839173, 15.5555703, -7.6922824, 8…
$ RENT3.SA <dbl> -3.1249929, -1.2882515, -5.1562278, 9.7701959, 7.9445975, -0…
$ SANB11.SA <dbl> -7.49999967, 4.89060343, -4.57144353, 0.71429856, -0.0644877…
$ SBSP3.SA <dbl> 7.4361397, -5.1175825, 8.4354465, 13.6103723, -1.5774985, -3…
$ SUZB3.SA <dbl> 0.0000000, 0.0000000, 0.0000000, 0.0000000, 0.0000000, 0.000…
$ TAEE11.SA <dbl> 13.9087829, -16.0177301, 20.9091071, 6.7669179, 3.5211227, 0…
$ TIMS3.SA <dbl> -1.8491505, -14.0211693, 14.4615424, -23.4766907, -6.4402964…
$ TOTS3.SA <dbl> 10.2373737, -1.7496546, 6.0273526, -2.3255395, 4.3650796, 6.…
$ UGPA3.SA <dbl> 8.2499698, -4.1801290, 8.9419339, 6.8583591, -8.5116603, 4.3…
$ USIM5.SA <dbl> -9.075774, -22.161174, -25.647056, 16.772159, 10.433597, 24.…
$ VALE3.SA <dbl> 1.7998567, -11.7605768, 6.7571101, -7.4258605, -9.0713231, 8…
$ VIVT3.SA <dbl> -2.915185, -9.940544, 3.777844, -2.434183, -11.440815, 2.005…
$ WEGE3.SA <dbl> 1.7171847, 3.2770939, -5.9780995, -4.4974075, 8.5899369, 17.…
$ YDUQ3.SA <dbl> 22.01691774, 6.30252417, -3.95256318, 3.82714815, 24.8513624…Aplicação
Code
n_obs <- nrow(retornos)
ins <- 90
oos <- n_obs - ins
Rp <- matrix(NA, ncol = 10, nrow = oos)
for (i in 1:oos) {
r <- retornos[i:(i + ins - 1), -1]
Sigma <- cov(r)
w_mv <- optimalPortfolio(Sigma, control = list(type = 'minvol', constraint = 'lo'))
w_iv <- optimalPortfolio(Sigma, control = list(type = 'invvol', constraint = 'lo'))
w_erc <- optimalPortfolio(Sigma, control = list(type = 'erc', constraint = 'lo'))
w_md <- optimalPortfolio(Sigma, control = list(type = 'maxdiv', constraint = 'lo'))
w_mdec <- optimalPortfolio(Sigma, control = list(type = 'maxdec', constraint = 'lo'))
w_hrp <- HRP_Portfolio(Sigma)$w
w_dhrp <- DHRP_Portfolio(Sigma)$w
w_hcaa <- HCAA_Portfolio(Sigma)$w
w_herc <- HERC_Portfolio(Sigma)$w
Rp[i, ] <- c(mean(as.numeric(retornos[i + ins, -1])),
sum(w_mv * retornos[i + ins, -1]),
sum(w_iv * retornos[i + ins, -1]),
sum(w_erc * retornos[i + ins, -1]),
sum(w_md * retornos[i + ins, -1]),
sum(w_mdec * retornos[i + ins, -1]),
sum(w_hrp * retornos[i + ins, -1]),
sum(w_dhrp * retornos[i + ins, -1]),
sum(w_hcaa * retornos[i + ins, -1]),
sum(w_herc * retornos[i + ins, -1]))
}[1] "Number of clusters: 7"
[1] "Number of clusters: 7"
[1] "Number of clusters: 7"
[1] "Number of clusters: 6"
[1] "Number of clusters: 6"
[1] "Number of clusters: 7"
[1] "Number of clusters: 5"
[1] "Number of clusters: 5"
[1] "Number of clusters: 5"
[1] "Number of clusters: 5"
[1] "Number of clusters: 5"
[1] "Number of clusters: 5"
[1] "Number of clusters: 5"
[1] "Number of clusters: 5"
[1] "Number of clusters: 5"
[1] "Number of clusters: 5"
[1] "Number of clusters: 5"
[1] "Number of clusters: 5"
[1] "Number of clusters: 5"
[1] "Number of clusters: 5"
[1] "Number of clusters: 6"
[1] "Number of clusters: 5"
[1] "Number of clusters: 6"
[1] "Number of clusters: 6"
[1] "Number of clusters: 5"
[1] "Number of clusters: 5"
[1] "Number of clusters: 5"
[1] "Number of clusters: 5"
[1] "Number of clusters: 6"
[1] "Number of clusters: 6"
[1] "Number of clusters: 6"
[1] "Number of clusters: 6"
[1] "Number of clusters: 5"
[1] "Number of clusters: 5"
[1] "Number of clusters: 5"
[1] "Number of clusters: 5"
[1] "Number of clusters: 5"
[1] "Number of clusters: 5"
[1] "Number of clusters: 6"
[1] "Number of clusters: 5"
[1] "Number of clusters: 6"
[1] "Number of clusters: 6"
[1] "Number of clusters: 5"
[1] "Number of clusters: 6"
[1] "Number of clusters: 6"
[1] "Number of clusters: 6"
[1] "Number of clusters: 6"
[1] "Number of clusters: 6"
[1] "Number of clusters: 6"
[1] "Number of clusters: 6"
[1] "Number of clusters: 6"
[1] "Number of clusters: 6"
[1] "Number of clusters: 6"
[1] "Number of clusters: 6"
[1] "Number of clusters: 6"Aplicação
Code
medidas <- function(x) {
# Annualized Average
AV <- mean(x)
# Annualized SD
SD <- sd(x)
# Information (or Sharpe) Ratio
SR <- mean(x)/sd(x)
# Adjusted Sharpe Ratio
ASR <- SR*(1 + (moments::skewness(x)/6)*SR - ((moments::kurtosis(x) - 3)/24)*SR^2)
# Sortino Ratio
SO <- mean(x)/sqrt(mean(ifelse(x < 0, 0, x^2)))
output <- c(12*AV, sqrt(12)*SD, sqrt(12)*SR, sqrt(12)*ASR, sqrt(12)*SO)
return(output)
}Aplicação
Code
AV SD SR ASR SO
EW 10.585417 28.03836 0.3775333 0.3698439 0.5406683
Min Var 13.658973 21.14320 0.6460221 0.6323241 0.8237391
Inv Vol 10.113954 25.93608 0.3899569 0.3815767 0.5565186
ERC 11.199226 24.85598 0.4505647 0.4408735 0.6268675
Max Div 13.233163 25.63452 0.5162243 0.5055968 0.6852115
Max Dec 13.879596 29.98986 0.4628096 0.4607294 0.5980135
HRP 9.800678 22.73546 0.4310745 0.4207513 0.6075124
DHRP 11.410010 22.64509 0.5038625 0.4891308 0.6968257
HCAA 14.883575 27.89803 0.5334992 0.5188800 0.7302500
HERC 17.693374 56.85116 0.3112228 0.3022183 0.4777920Tópicos de pesquisa
Tópicos de pesquisa
- Custos de transação / Otimização
- Outros estimadores da matriz de covariância
- Variância (covariância) condicional
- Dados em alta dimensão
- Dados em alta frequência
- Metodologias híbridas

Carlos Trucíos (IMECC/UNICAMP) | Semana da Estatística UFJF 2024 | Risk-Based Portfolio Allocation | ctruciosm.github.io