Inferência Causal

Ignorabilidade e sobreposição

Prof. Carlos Trucíos
ctrucios@unicamp.br

Instituto de Matemática, Estatística e Computação Científica (IMECC),
Universidade Estadual de Campinas (UNICAMP).

Introdução

Até agora, temos discutido como estimar efeitos causais em estudos observacionais assumindo ignorabilidade e sobreposição.
Contudo, na prática, ambas suposições são bastatnte fortes e são violadas na prática.
Aprenderemos quais as implicações e como lidar com este problema.

Diagramas

Diagramas causais ou DAGs (directed acyclic graph) foram introduzidos por Pearl (1995).
São uma ferramenta valiosa na inferência causal.
Utilizaremos estes diagramas como uma forma intuitiva de ilustrar as relações causais entre variáveis.

Diagramas

Exemplo 1

Se tivermos o diagrama ao lado e o foco for o efeito causal de \(Z\) sob \(Y\), estamos dizendo que o processo gerador de dados é da forma:

\[\begin{align} &X \sim F_X(x), \\ &Z = f_Z(X, \epsilon_Z), \\ &Y(z) = f_Y(X, z, \epsilon_y(z)), \end{align}\] em que \(\epsilon_Z \perp\!\!\!\perp \epsilon_Y(z)\). Ademais, é fácil ver \(Z \perp\!\!\!\perp Y(z) | X\)

Diagramas

Exemplo 2

\[\begin{align} &X \sim F_X(x), \\ &U \sim F_U(u), \\ &Z = f_Z(X, U, \epsilon_Z), \\ &Y(z) = f_Y(X, U, z, \epsilon_y(z)), \end{align}\] em que \(\epsilon_Z \perp\!\!\!\perp \epsilon_Y(z)\). Ademais, é fácil ver \(Z \perp\!\!\!\perp Y(z) | (X, U)\) (ignorabilidade acontece condicionado em \((X, U)\) mas não condicionado apenas em \(X\)).

\(U\) é uma variável de confusão não medida.

Avaliando inconfundibilidade

A suposição de ignorabilidade (também conhecida, inconfundibilidade) é dada por \[Z \perp\!\!\!\perp Y(1) | X \quad e \quad Z \perp\!\!\!\perp Y(0) | X,\] o que implica que \[\begin{align} P(Y(1) | Z = 1, X) & = P(Y(1) | Z = 0, X), \\ P(Y(0) | Z = 1, X) & = P(Y(0) | Z = 0, X). \end{align}\]

Ou seja, que as distribuições dos contrafactuais \(P(Y(1) | Z = 0, X)\) e \(P(Y(0) | Z = 1, X)\) sejam as mesmas do que as distribuições dos factuais \(P(Y(1) | Z = 1, X)\) e \(P(Y(0) | Z = 0, X)\)!.

Avaliando inconfundibilidade

Sem suposições adicionais, não é possível testar a suposição de ignorabilidade.
Contudo, aprenderemos duas estratégias para avaliar a suposição de ignorabilidade:
- negative outcomes
- negative exposures

Avaliando inconfundibilidade: negative outcomes

Suponha que \(Yn\) é similar a \(Y\) (idealmente, compartilha a mesma estrutura de confusão).
Se \(Z \perp\!\!\!\perp Y(z) | X\) então \(Z \perp\!\!\!\perp Yn(z) | X\)
\(Yn\) deve ser de tal forma que conheçamos, a priori, o efeito de \(Z\) sob \(Yn\): \[\tau(Z \rightarrow Yn) = \mathbb{E}[Yn(1) - Yn(0)],\] sendo um exemplo importante quanto \(\tau(Z \rightarrow Yn) = 0.\)
Qual seria um diagrama que satisfaz esses requerimentos?

Avaliando inconfundibilidade: negative outcomes

Exemplo 1

Cornfield et al. (1959) estudaram o efeito de fumar cigarros no câncer de pulmão através de um estudo observacional. Os autores incluiram diversar covariáveis mas ainda existe a possibilidade de termos uma variável de confusão não medida que pode causar vies no efeito observado.

Para fortalecer as evidências de causalidade, os autores também reportaram o efeito de fumar cigarros sob accidentes de auto (que foi perto de zero, como esperado). Assim, as análises baseadas no negative outcomes fazem com que a evidência de causalidade entre fumar cigarros no câncer de pulmão de torne-se mais forte.

Negative outcomes consiste em, utilizando \(Yn\) e sabendo que o efeito causal de \(Z\) sob \(Yn\) é nulo, verificar através dos dados, se é nulo mesmo. Desta forma, descartamos que o efeito causal de \(Z\) sob \(Y\) seja por causa de uma variável de confusão não medida.

Avaliando inconfundibilidade: negative outcomes

Exemplo 2

Imbens e Rubin (2015) sugerem utilizar o resultado defasado como negative outcome.

Em muitos casos, é razoável acreditar que o resultado defasado e o resultado tem a mesma estrutura de confusão.

Como o resultado defasado acontece antes do tratamento, o efeito causal médio deve ser 0.

Avaliando inconfundibilidade: negative outcomes

Exemplo 3

Um estudo observacional com pessoas idosas mostrou que vacina contra a influenza reduz o risco de pneumonia/hospitalização por influenza, bem como mortalidade (por todas as causas) na temporarada seguinte.

Jackson et al. (2006), duvidando das conclusões, realizam uma análise suplementar com negative outcomes.

Vacinação começa outono e a transmisão da influenza é minima até o inverno. Assim, o efeito da vacinação deve ser mais proominente durante a época de influenza. Contudo, Jackson et al. (2006) encontram um efeito maior antes do período de influenza, sugerindo que o efeito observado é, na verdade, devido a variáveis de confusão não observadas.

Negative outcomes é uma estratégia interessante. Contudo, encontrar \(Yn\) não é trivial e precisa de um amplo conhecimento do problema em estudo.

Avaliando inconfundibilidade: negative expousures

Assuma que \(Zn\) é similar a \(Z\) (idealmente compartilha a mesma estrutura de confusão).
Se \(Z \perp\!\!\!\perp Y(z) | X\) então \(Zn \perp\!\!\!\perp Y(z) | X\)
Ademais, conhecemos, a priori, o efeito de \(Zn\) sob \(Y\): \[\tau(Zn \rightarrow Y) = \mathbb{E}[Y(1^n) - Y(0^n)].\]
Um exemplo importante é quando \(\tau(Zn \rightarrow Y) = 0\). Qual seria o dirgamra que satisfaz estes requerimentos?

Avaliando inconfundibilidade: negative expousures

Exemplo 4

Sanderson et al. (2017) dão muitos exemplos de negative expousures na determinação do efeito da exposição intrauterina nos resultados posteriores. Eles comparam a associação da exposição materna durante a gravidez com o resultado de interesse, com a associação da exposição paterna com o mesmo resultado. Eles revisam estudos sobre o efeito do tabagismo materno e paterno nos resultados dos filhos, e estudos sobre o efeito do IMC materno e paterno no IMC dos filhos e no transtorno do espectro autista. Nestes exemplos, esperamos que a associação da exposição materna (\(Z\)) com o resultado seja maior do que a da exposição paterna (\(Zn\)) com resultado.

Avaliando inconfundibilidade:

Alguns comentários:

Testar inconfundibilidade não é possível, mas podemos utilizar negative outcomes ou negative exposures como análise suplementar a fortalecer a nossa evidência sobre causalidade.
Contudo, utilizar esta abordagem não é trivial, principalmente, por dois motivos:
- Requer mais dados (que nem sempre teremos)
- Requer um amplo conhecimento do problema em análise para saber escolher bem \(Yn\) ou \(Zn\).

Sobreajuste

Nas aulas anteriores discutimos como estimar efeitos causais sob e suposição de inconfundibilidade ou ignorabilidade:

\[Z \perp\!\!\!\perp \{ Y(1), Y(0) \} | X\]

Nesta suposição, é vital escolhermos o conjunto certo de covariáveis \(X\). Mas, qual é esse conjunto certo?

Todas as variáveis pre-tratamento [Rosembaum (2002) e Rubin (2007)].
Contudo, não todos concordam com esta abordagem. De fato, Pearl da dois contraexemplos.

Sobreajuste

M-vies

M-vies aparece no seguinte DAG (com forma de “M”).

em que \(X\) é observado mas \(U1\) e \(U2\) não são.

Sobreajuste

M-vies

\(U1 \perp\!\!\!\perp U2\),
\(Z = f_Z(U1, \epsilon_z)\),
\(X = f_X(U1, U2, \epsilon_x)\),
\(Y = Y(z) = f_Y(U2, \epsilon_y)\),
\((\epsilon_z, \epsilon_x, \epsilon_y)\) são termos aleatórios independentes.

Note que se mudarmos o valor de \(Z\), o valor de \(Y\) não muda. Ou seja, o verdadeiro efeito causal de de \(Z\) sob \(Y\) é zero.

Sobreajuste

M-vies

Ademais, \[\tau_{PF} = \mathbb{E}[Y | Z = 1] - \mathbb{E}[Y | Z = 0] = 0\]

Isto significa que, sem ajustar por covariáveis, teremos um estimador não viesado para o verdadeiro valor do parâmetro.

Sobreajuste

M-vies

Suponha que:

\(X = aU_1 + b U_2 + \epsilon_X\),
\(Z = cU_1 + \epsilon_Z\),
\(Y = dU_2 + \epsilon_Y\),
\((U_1, U_2, \epsilon_X, \epsilon_Z, \epsilon_Y) \sim N(0,1)\)

\[\mathbb{C}ov(Z, Y) = \mathbb{C}ov(cU_1 + \epsilon_Z, dU_2 + \epsilon_Y) = 0\]

Contudo, \[\rho_{ZY|X} = \dfrac{\rho_{ZY} - \rho_{ZX}\rho_{YX}}{\sqrt{1 - \rho^2_{ZX}} \sqrt{1 - \rho^2_{YX}}} \propto -\mathbb{C}ov(Z, X) \mathbb{C}ov(Y, X) \propto -abdc\]

Sobreajuste

M-vies

Code

n <- 10^6
U1 <- rnorm(n)
U2 <- rnorm(n)
X <- U1 + U2 + rnorm(n)
Y <- U2 + rnorm(n)
Z <- U1 + rnorm(n)
tau <- summary(lm(Y ~ Z))$coef[2, 1]
tau_adj <- summary(lm(Y ~ Z + X))$coef[2, 1]
round(c(tau, tau_adj), 3)

[1]  0.001 -0.199

O estimador simples é não viesado, mas o ajustado por covariáveis é viesado.

Ou seja, neste caso, condicionar por todas as covariáveis pre-tratamento não é benéfico 😢.

Em geral, quando o PGD é da forma do diagrama apresentado anteriormente (com forma de “M”), condicionar por todas as covariáveis pre-tratamento causará um vies.

Sobreajuste

Z-vies

Consideremos o seguinte diagrama causal:

Sobreajuste

Z-vies

Suponha que:

\(Z = aX + bU + \epsilon_Z,\)
\(Y(z) = \tau z + cU + \epsilon_y\)
\((U, X, \epsilon_Z, \epsilon_Y) \sim N(0,1)\)

\[\tau_{unAdj} = \dfrac{\mathbb{C}ov(Z, Y)}{\mathbb{V}(Z)} = \tau + \dfrac{bc}{a^2 + b^2 + 1}\]

\[\tau_{Adj} = \tau + \dfrac{bc}{b^2 + 1}\]

Sobreajuste

Z-vies

Code

n <- 10^6
X <- rnorm(n)
U <- rnorm(n)
a <- 1
Z <- a*X + U + rnorm(n)
Y <- U + rnorm(n)
tau_unadj <- summary(lm(Y ~ Z))$coef[2, 1]
tau_adj <- summary(lm(Y ~ Z + X))$coef[2, 1]
round(c(tau_unadj, tau_adj), 3)

[1] 0.333 0.499

Code

a <- 5
Z <- a*X + U + rnorm(n)
tau_unadj <- summary(lm(Y ~ Z))$coef[2, 1]
tau_adj <- summary(lm(Y ~ Z + X))$coef[2, 1]
round(c(tau_unadj, tau_adj), 3)

[1] 0.037 0.499

Code

a <- 10
Z <- a*X + U + rnorm(n)
tau_unadj <- summary(lm(Y ~ Z))$coef[2, 1]
tau_adj <- summary(lm(Y ~ Z + X))$coef[2, 1]
round(c(tau_unadj, tau_adj), 3)

[1] 0.010 0.498

Ou seja, neste caso, condicionar por todas as covariáveis pre-tratamento não é benéfico 😭.

Sobreajuste

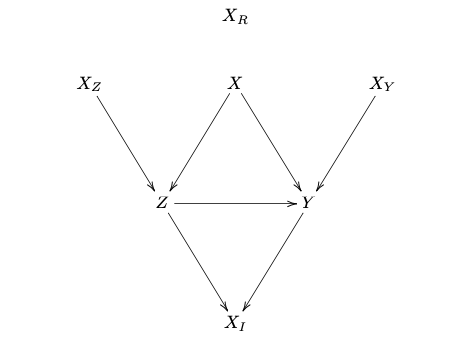
Quais variáveis, devem, então, estar em \(X\)?

Sobreajuste

\(X\) afeta tanto \(Z\) quanto \(Y\). Condicionar em \(X\) garante ignorabilidade. Assim, devemos controlar por \(X\).
\(X_R\) é um ruido e não afeta nem \(Z\) nem \(Y\). Incluir \(X_R\) não trará vies mas aumentará a variância (o velho problema de inclur variáveis irrelevantes)
\(X_Z\) afeta o resultado apenas através de \(Z\). Incluí-lo na análise não trará vies mas aumentará a variância. Contudo, com variáveis de confusão não medidas, aumenta o vies.
\(X_Y\) afeta o resultado mas não o tratamento. Sem condicional nela, ignorabilidade ainda acontece. Como ela é preditiva do resultado, incluí-la aumentará a precisão.
\(X_I\) é afetada pelo tratamento e pelo resultado (é uma variável pós-tratamento, não pre-tratamento). Não devemos incluir esta variável.

Devemos incluir \(X\) para remover o vies e \(X_Y\) para reduzir variância.

Referências

Peng Ding (2023). A First Course in Causal Inference. Capítulo 16.
Lipsitch, M., Tchetgen, E. T., & Cohen, T. (2010). Negative controls: a tool for detecting confounding and bias in observational studies. Epidemiology, 21(3), 383-388.