Code
[1] 19.857227 8.792532Regressão não linear
Instituto de Matemática, Estatística e Computação Científica (IMECC),
Universidade Estadual de Campinas (UNICAMP).
Exemplo
Seja o modelo \[y_i = \underbrace{f(x_i, \beta)}_{x_i(\beta)} + u_i, \quad u_i \sim IID(0, \sigma^2), \quad i = 1, \cdots, n,\] em que \(x_i(\beta)\) é chamada função de regressão não linear.
Equivalentemente, \[\textbf{Y} = \textbf{X}(\beta) + \textbf{u}, \quad \textbf{u} \sim IID(0, \sigma^2I)\]
Seja o modelo \[y_i = \beta_0 + \beta_1 x_{i1} + \dfrac{1}{\beta_1} x_{i2} + u_i, \quad u_i \sim IID(0, \sigma^2).\]
A função de regressão não linear é dada por \(x(\beta) = \beta_0 + \beta_1 x_1 + \dfrac{1}{\beta_1}x_2\).
Seja o MRL com erros AR(1): \[\begin{align} y_t &= \textbf{X}_t \beta + u_t, \\ u_t &= \rho u_{t-1} + \epsilon_t, \\ \epsilon_t &\sim IID(0, \sigma^2) \end{align}\]
No caso dos modelos de regressão linear, temos:
No caso dos modelos de regressão não linear, teremos:
Observação
Existem (pelo menos) duas formas de aproximar o assintóticamente eficiente, mas inviável, MM que utiliza \(\textbf{W} = \textbf{X}_0 = \textbf{X}_0(\beta)\).
Forma 1:
Forma 2
Considerar a condição de momentos \[\textbf{X}'_0(\beta)(\textbf{y} - x(\beta)) = 0.\]
Pode-se provar que a condição de momentos é equivalente a minimizar \[SQR(\beta) = \displaystyle \sum_{t = 1}^n (y_t - x_t(\beta))' (y_t - x_t(\beta))\]
Exemplo
Utilizaremos um conjunto de dados simulados em que \[y = (a*x)/(b + x),\] e queremos estimar um modelo que captura propriadamente a dinâmica dos dados.
Formula: y ~ a * x/(b + x)
Parameters:
Estimate Std. Error t value Pr(>|t|)
a 19.7063 0.1219 161.65 <2e-16 ***
b 8.4538 0.2831 29.86 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.027 on 399 degrees of freedom
Number of iterations to convergence: 6
Achieved convergence tolerance: 3.797e-08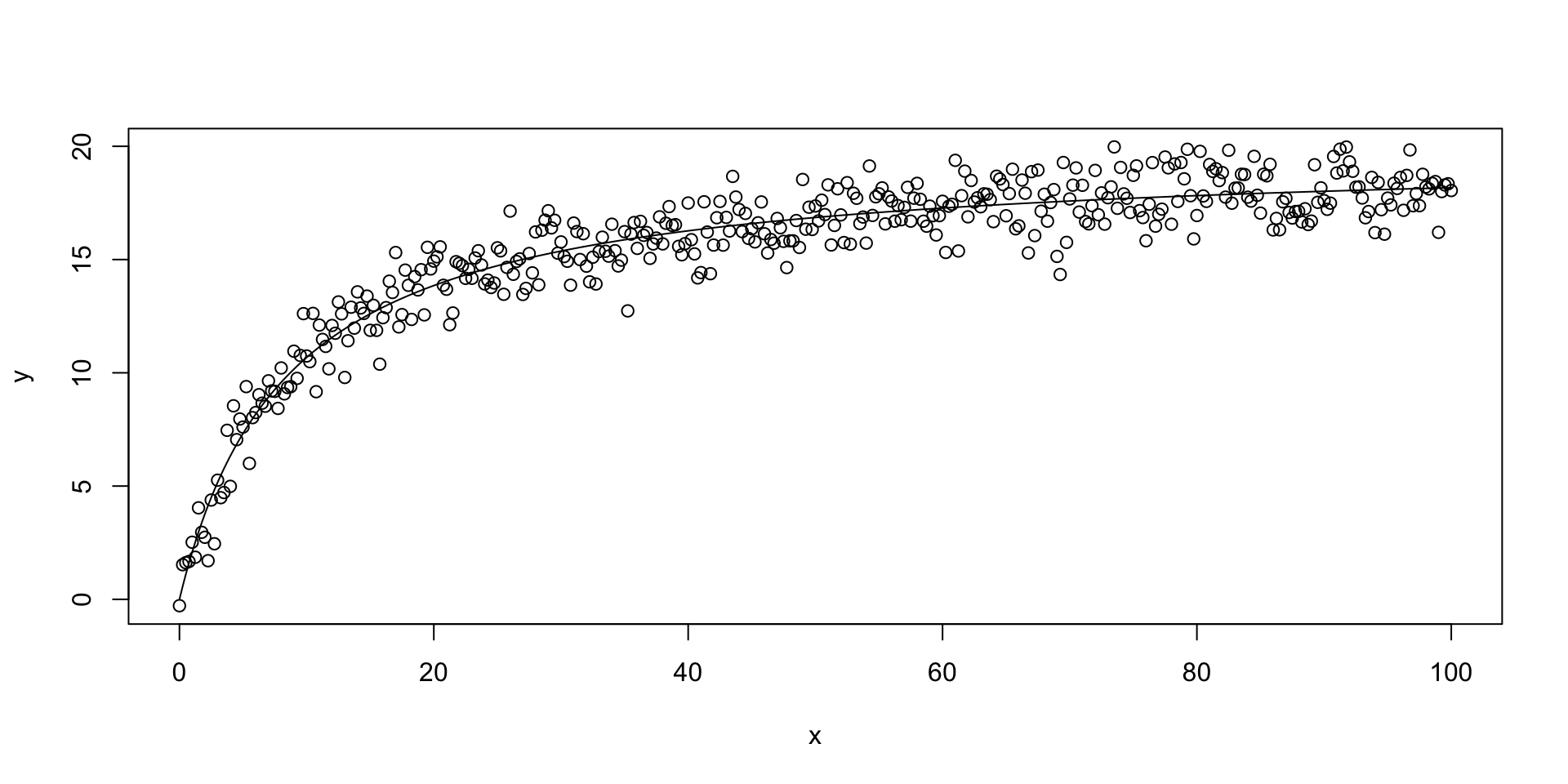

Carlos Trucíos (IMECC/UNICAMP) | ME715 - Econometria | ctruciosm.github.io