ME715 - Econometria

Modelo de Regressão Linear II

Prof. Carlos Trucíos
ctrucios@unicamp.br

Instituto de Matemática, Estatística e Computação Científica (IMECC),
Universidade Estadual de Campinas (UNICAMP).

Outras propriedades

Outras propriedades

Hipóteses do modelo

Note

• HRLM1: O modelo populacional é linear nos parâmetros, \(Y = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \ldots + \beta_k X_k + u\) (equivalentemente, em forma matricial, \(Y = \textbf{X} \beta + \textbf{u}\)).
• HRLM2: \((Y_1, X_{1,1}, \ldots, X_{1,k}), \cdots, (Y_n, X_{n,1}, \ldots, X_{n,k})\) constituem uma a.a. de tamanho \(n\) do modelo populacional.
• HRLM3: Não existe colinearidade perfeita entre as variáveis independentes e nenhuma das variáveis independentes é constante.
• HRLM4: \(\mathbb{E}(\textbf{u}|\textbf{X}) = 0\)
• HRLM5: Os erros tem variância constante (homocedasticidade), \(\mathbb{V}(\textbf{u}|\textbf{X}) = \sigma^2 \textbf{I}\)

Além ds hipóteses já vistas, a seguinte hipótese é algumas vezes também utilizada.

HRLM6: \(u\) é independente das variáveis explicativas e \(u | \textbf{X} \sim N(0,\sigma^2 I)\).

HRLM1–HRLM6 são conhecidas como as hipóteses do modelo linear clássico.

Outras propriedades

Sob HRLM1–HRLM6, condicional em \(\textbf{X}\):

\[\hat{\beta} - \beta \sim N(0, \sigma^2 (X'X)^{-1}),\]

\[\dfrac{(n-k-1)s^2}{\sigma^2}\sim \chi^2_{n-k-1},\]

\[\dfrac{\hat{\beta}_j - \beta_j}{\sqrt{\widehat{\mathbb{V}}(\hat{\beta}_j|X)}} \sim t_{n-k-1},\]

em que \(s^2 = \dfrac{\hat{u}' \hat{u}}{n-k-1}\) e \(\widehat{\mathbb{V}}(\hat{\beta}|X) = s^2 (X'X)^{-1}.\)

Propriedades Assintóticas do EMQO

Propriedades Assintóticas do EMQO

Teoria assintótica nos permite relaxar algumas suposições do modelo necessárias para obter a distribuição amostral dos estimador desde que o tamanho amostral seja suficientemente grande.

Distribuições amostrais são importantes pois nos permitem obter intervalos de confiança e realizar testes de hipóteses sobre \(\beta\).

Duas propriedades interessante são:

\[\hat{\beta} \rightarrow_p \beta \quad e\] \[\hat{\beta} - \beta \rightarrow_d N(0, \sigma^2 (X'X)^{-1})\]

Propriedades Assintóticas do EMQO

Para ilustrar a primeira propriedade, pense no seguinte DGP.

Code

n <- 50000
u <- rnorm(n)
x <- runif(n)
y <- 0.9 + 1.3*x + u
j <- 1
beta <- matrix(NA, ncol = 2, nrow = 5000)
for (i in seq(10, n, by = 10)) {
  beta[j,] <- c(i, coef(lm(y[1:i]~x[1:i]))[2])
  j <- j + 1
}
plot(beta, type = "l", ylab = expression(hat(beta)[1]), xlab = "n")
abline(h = 1.3, col = "red")

Propriedades Assintóticas do EMQO

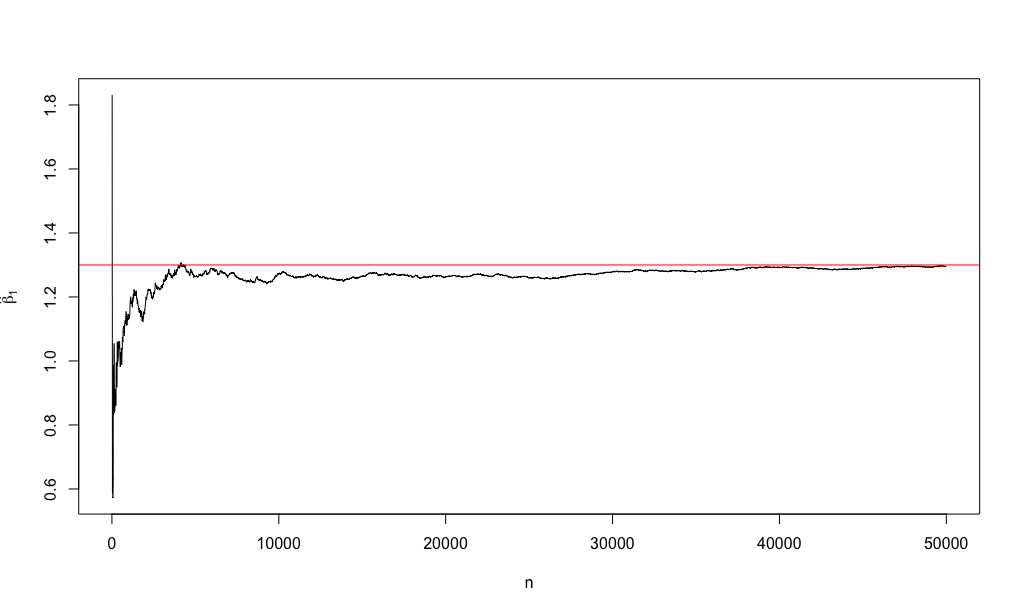
Propriedades Assintóticas do EMQO

Para ilustrar a segunda, pense no seguinte:

Code

library(ggplot2)
library(tidyr)
n <- 100
mc <- 100000
b0 <- 1
b1 <- 0.7
b_hat <- matrix(NA, ncol = 2, nrow = mc)
x <- rnorm(n, 4, 1)
for (i in 1:mc) {
  u <- rnorm(n)
  y <- b0 + b1*x + u
  b_hat[i, 1] <- as.numeric(coef(lm(y~x)))[2]
}
X <- matrix(c(rep(1, n), x), n, 2)
b_hat[, 2] <- rnorm(mc, 0.7, sqrt(solve(t(X) %*% X)[2,2]))
colnames(b_hat) <- c("beta_hat", "normal")
b_hat <- b_hat |> data.frame() |> pivot_longer(cols = everything(), names_to = "betas", values_to = "values")
ggplot(b_hat, aes(x = values, group = betas, color = betas)) + geom_density()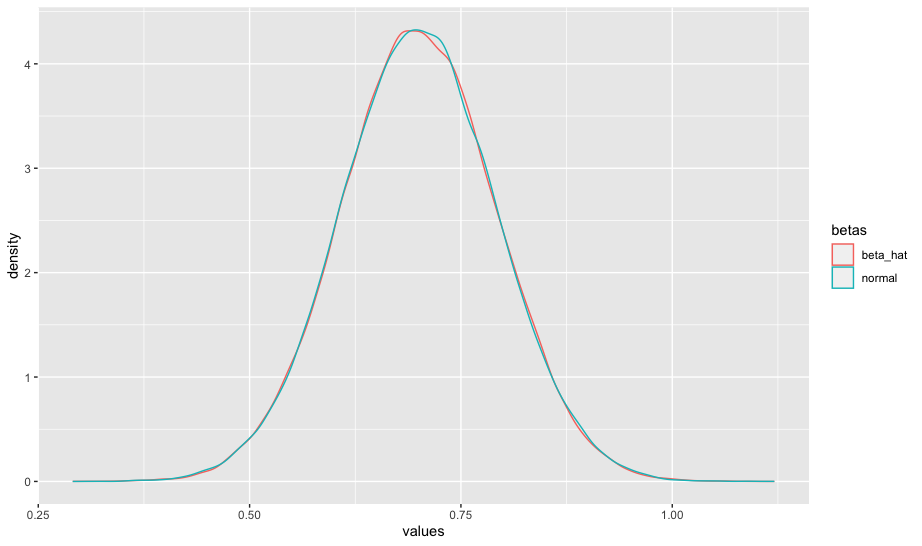

Propriedades Assintóticas do EMQO

1. O que é de se esperar se utilizarmos \(n = 25\)?
2. O que é de se esperar se utilizarmos \(n = 1000\)?
3. O que é de se esperar se utilizarmos \(n = 25\) e \(u = \dfrac{v-1}{\sqrt{2}}\), em que \(v \sim X^2_1\)?
4. O que é de se esperar se utilizarmos \(n = 100\) e \(u = \dfrac{v-1}{\sqrt{2}}\), em que \(v \sim X^2_1\)?
5. O que é de se esperar se utilizarmos \(n = 1000\) e \(u = \dfrac{v-1}{\sqrt{2}}\), em que \(v \sim X^2_1\)?

Propriedades Assintóticas do EMQO

• HRLM1–HRLM6 garante que \(\hat{\beta}\) seja normalmente distribuiía (independentemente do tamanho amostral).
• A convergência em distribuição (teoria assintótica) nos diz que, mesmo que \(u\) não tenha uma distribuição normal, \(\hat{\beta}\) será normalmente distribuida desde que o tamanho amostral seja grande.

Unidades de medida

Unidades de medida

Se a variável independente for dividida/multiplicada por uma constante \(c \neq 0\), então o \(\hat{\beta}\) associado a essa variável será multiplicado ou dividido por \(c\).

Code

n <- 100
u <- rnorm(n)
x <- rnorm(n)
y <- 1.7 + 1.2*x + u
c <- 5
x_n <- x/c
coef(lm(y~x))

(Intercept)           x 
   1.405688    1.146386 

Code

coef(lm(y~x_n))

(Intercept)         x_n 
   1.405688    5.731928 

Code

coef(lm(y~x))[2]*c

       x 
5.731928 

Unidades de medida

Mudar as unidades de medida da variável independente não muda \(\hat{\beta}_0\).

Code

n <- 100
u <- rnorm(n)
x <- rnorm(n)
y <- 1.7 + 1.2*x + u
c <- 5
x_n <- x/c
coef(lm(y~x))

(Intercept)           x 
   1.486434    1.091008 

Code

coef(lm(y~x_n))

(Intercept)         x_n 
   1.486434    5.455040 

Unidades de medida

Mudanças de unidade de medida não alteram o \(R^2\) (a qualidade de ajuste do modelo não depende das unidades de medida).

Code

summary(lm(y~x))

Call:
lm(formula = y ~ x)

Residuals:
    Min      1Q  Median      3Q     Max 
-3.1844 -0.5727 -0.0363  0.6700  1.9335 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  1.48643    0.09832   15.12   <2e-16 ***
x            1.09101    0.09510   11.47   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.9825 on 98 degrees of freedom
Multiple R-squared:  0.5732,    Adjusted R-squared:  0.5688 
F-statistic: 131.6 on 1 and 98 DF,  p-value: < 2.2e-16

Code

summary(lm(y~x_n))

Call:
lm(formula = y ~ x_n)

Residuals:
    Min      1Q  Median      3Q     Max 
-3.1844 -0.5727 -0.0363  0.6700  1.9335 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  1.48643    0.09832   15.12   <2e-16 ***
x_n          5.45504    0.47549   11.47   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.9825 on 98 degrees of freedom
Multiple R-squared:  0.5732,    Adjusted R-squared:  0.5688 
F-statistic: 131.6 on 1 and 98 DF,  p-value: < 2.2e-16

Unidades de medida

Quando mudamos as unidades de medida da variável (seja esta independente ou dependente) quando ela aparece em escala logarítmica, nada acontece com a inclinação mas o intercepto muda.

Code

n <- 100
u <- rnorm(n)
x <- runif(n, 1, 20)
y <- 1.7 + 1.2*x + u
c <- 5
x_n <- x/c
coef(lm(y~log(x)))

(Intercept)      log(x) 
  -4.421139    8.590856 

Code

coef(lm(y~log(x_n)))

(Intercept)    log(x_n) 
   9.405310    8.590856 

Não linearidades

Não linearidades

• Em geral, relações lineares não são suficientes para todas as aplicações.
• Duas opções simples para incluir não linearidades são: (a) aplicar \(\log(\cdot)\), (b) incluir termos polinomiais.
• Em termos de estimação, nada muda. Contudo, devemos nos atentar à interpretação do modelo.

Não linearidades

Transformação logarítmica

• A transformação pode linearizar a variável
• Gera um modelo com (aproximadamente) um efeito percentual constante \(\log(y) = \beta_0 + \beta_1 x + u\)
• \(\Delta \log(y) = \log(y_1) - \log(y_0) \approx (y_1-y_0)/y_0 = \Delta y/y_0\), então \[100 \times \Delta \log(y) \approx \% \Delta y\]
• Logo, se \(\Delta u = 0\), temos que \[\% \Delta y \approx 100 \times \Delta \log(y) = (100 \beta_1) \Delta x\]

(para uma revisão de \(\log(\cdot)\) ver Apêndice A.4b)

Não linearidades

Modelo	V. Dependente	V. Independente	Interpretação \(\beta_1\)
Nível-Nível	\(y\)	\(x\)	\(\Delta y = \beta_1 \Delta x\)
Nível-Log	\(y\)	\(\log(x)\)	\(\Delta y = \big(\beta_1/100 \big) \% \Delta x\)
Log-Nível	\(\log(y)\)	\(x\)	\(\% \Delta y = 100\beta_1 \Delta x\)
Log-Log	\(\log(y)\)	\(\log(x)\)	\(\% \Delta y = \beta_1 \% \Delta x\)

Não linearidades

Exemplo: O dataset wage1 do pacote wooldridge contém informação de 526 pessoas. A variável wage é o salário médio por hora e a variável educ são os anos de educação formal.

Ajustando um modelo RLS \[\log(wage) = \beta_0 + \beta_1 educ + u\], obtemos:

Code

library(wooldridge)
coef(lm(log(wage)~educ, data = wage1))

(Intercept)        educ 
 0.58377267  0.08274437 

Qual interpretação é correta?

• A cada ano adicional de educação, o salário médio por hora aumenta em \(\approx\) 0.0827 USD
• A cada ano adicional de educação, o salário médio por hora aumenta em \(\approx\) 8.27%

Não linearidades

Exemplo: O dataset hprice2 do pacote wooldridge contém informação de 506 comunidades na área de Boston nos Estados Unidos. As variáveis price, nox, rooms, dist e stratio representam o preço médio das casas, quantidade de óxido nitroso no ar, número médio de cômodos nas casas da comunidade, distância média ponderada da comunidade em relação às cinco centrais de emprego e a razão média estudante-professor nas escolas da comunidade. Se ajustarmos o modelo \[\log(price) = \beta_0 + \beta_1 \log(nox) + \beta_2 rooms + \beta_3 \log(dist) + \beta_4 stratio + u\], obtemos:

Code

coef(lm(log(price) ~ log(nox) + rooms, data = hprice2))

(Intercept)    log(nox)       rooms 
  9.2337378  -0.7176735   0.3059183 

Como interpretaria \(\hat{\beta}_1\)?

A cada aumento de 1% na quantidade de óxido nitroso no ar, o preço médio da casa diminui em \(\approx\) 0.72 %.

Não linearidades

Exemplo: O dataset MEAP93 do pacote wooldridge contém informação de 408 escolas de Ensino Médio do estado de Michigan em 1993.

Se ajustarmos o modelo \[math10 = \beta_0 + \beta_1 \log(expend) + \beta_2lnchprg + u,\] obtemos:

(Intercept) log(expend)     lnchprg 
-20.3608165   6.2296983  -0.3045853 

Qual a interpretação de \(\hat{\beta}_1\)?

Quando expend aumenta em 1%, math10 aumenta em \(\approx\) 0.063 (\(\hat{\beta}_1/100\)).

Não linearidades

Muitas vezes, para tentar capturar não-linearidades, podemos estar interessados em incluir, por exemplo \(X_k^2\), \(X_k^3\) …, \[Y = \beta_0 + \beta_1 X_1 + \beta_2 X_1^2 + \beta_3 X_2 + \beta_4X_3 + \beta_5X_4+u\]

No contexto de MRLM podemos incluir termos polinomiais. O processo de estimação continua sendo o mesmo mas devemos ter muito cuidado na interpretação.

Por exemplo, pense no seguinte modelo

\[\begin{equation}\label{quadratica} \hat{Y} = \hat{\beta}_0 + \hat{\beta}_1X + \hat{\beta}_2X^2 \end{equation}\]

• Se estivermos interessados unicamente em predição, não há maiores complicações.
• Se estivermos interessados em conhecer o efeito de \(X\) sobre \(Y\) precisamos interpretar o modelo.

Não linearidades

Se ajustarmos o seguinte modelo

\[wage = \beta_0 + \beta_1 exper + \beta_2 exper^2 + u,\]

obtemos:

Code

coef(lm(wage~ exper + I(exper^2), data = wage1))

 (Intercept)        exper   I(exper^2) 
 3.725405759  0.298100104 -0.006129887 

O que acha da seguinte interpretação?

Se exper aumenta em uma unidade, wage aumenta em 0.29 (mantendo todos os outros fatores fixos).

Como podemos manter \(exper^2\) fixo se \(exper\) está aumentando?

A correta interpretação precisa ser muito mais cuidadosa.

Não linearidades

\[\hat{y} = \hat{\beta}_0 + \hat{\beta}_1x + \hat{\beta}_2x^2\]

Derivando w.r.t \(X\), temos que \(\dfrac{d\hat{y}}{dx} = (\hat{\beta}_1 + 2 \hat{\beta}_2x)\), então \[\dfrac{\Delta \hat{y}}{ \Delta x} \approx (\hat{\beta}_1 + 2 \hat{\beta}_2x)\]

• Se \(x=0\), \(\dfrac{\Delta \hat{y}}{ \Delta x} \approx \hat{\beta}_1\), \(\hat{\beta}_1\) pode ser interpretado como a inclinação aproximada na alteração de \(x=0\) para \(x=1\)
• Para \(x>0\), \(2 \hat{\beta}_2x\) deve ser considerado na interpretação

Não linearidades

Code

coef(lm(wage~ exper + I(exper^2), data = wage1))

 (Intercept)        exper   I(exper^2) 
 3.725405759  0.298100104 -0.006129887 

Como varia wage em função de exper? \[\Delta \hat{y} \approx (0.2981 - 2 \times 0.0061x) \Delta x\]

• O primeiro ano a experiência vale 0.2981 USD por hora
• Depois do primeiro ano, o efeito de experiência começa a cair:
  • Para o segundo ano: \(0.2981 - 2 \times 0.0061(1) = 0.2859\)
  • Para o terceiro ano: \(0.2981 - 2 \times 0.0061(2) = 0.2737\)
  • Para o décimo ano: \(0.2981 - 2 \times 0.0061(9) = 0.1883\)
• Note que o ponto de inflexão é \(x* = - \hat{\beta}_1 / 2 \hat{\beta}_2\), no nosso caso \(x* = 0.2981/(2 \times 0.0061) = 24.43\)

Não linearidades

\[\hat{y} = 3.73 + 0.2981 x - 0.0061 x^2\]

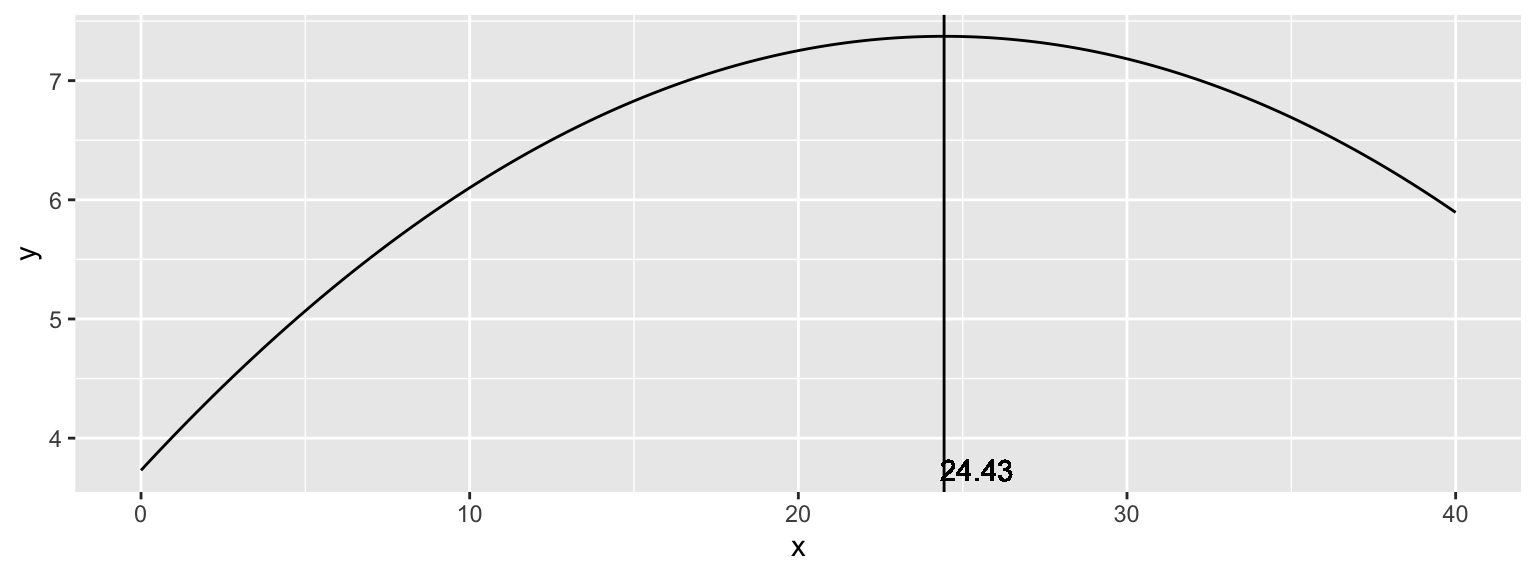
Não linearidades

O que significa esse 24.43 anos?

• Se na amostra, apenas uma pequena fração dos dados apresentam exper > 24.43, não devemos nos preocupar.

Code

prop.table(table(wage1$exper > 24.43))

    FALSE      TRUE 
0.7205323 0.2794677 

O que pode estar acontecendo?

• É possivel que o retorno de exper sobre wage seja negativo a partir de algum ponto, mas cuidado com as variáveis omitidas! (levam a estimadores viesados).

Qualidade de ajuste

R2

\[\underbrace{\displaystyle \sum_{i=1}^n (y_i - \bar{y})^n}_{SQT} = \underbrace{\sum_{i=1}^n (\hat{y}_i - \bar{y})^2}_{SQE} + \underbrace{\sum_{i=1}^n \hat{u}_i^2}_{SQR}\]

\[R^2 = 1- SQR/SQT = SQE/SQT\]

• \(R^2:\) proporção da variabilidade de \(y\) que é explicada pelo modelo.
• \(100 \times R^2:\) porcentagem da variabilidade de \(y\) que é explicada pelo modelo.

R2

Code

modelo1 = lm(log(wage)~educ,data = wage1)
modelo2 = lm(log(wage)~educ+exper,data = wage1)
modelo3 = lm(log(wage)~educ+exper+tenure,data = wage1)
modelo4 = lm(log(wage)~educ+exper+tenure+nonwhite,data = wage1)
modelo5 = lm(log(wage)~educ+exper+tenure+nonwhite
             +female,data = wage1)
modelo6 = lm(log(wage)~educ+exper+tenure+nonwhite
             +female + married,data = wage1)
modelo7 = lm(log(wage)~educ+exper+tenure+nonwhite+female
             +married+numdep,data = wage1)

R2

Code

modelo = 1:7
R2 = c(summary(modelo1)$r.squared, summary(modelo2)$r.squared,
       summary(modelo3)$r.squared, summary(modelo4)$r.squared,
       summary(modelo5)$r.squared, summary(modelo6)$r.squared,
       summary(modelo7)$r.squared)

dados = data.frame(R2, modelo)
library(ggplot2)
ggplot(dados, aes(y = R2, x = modelo)) + geom_line() + geom_point()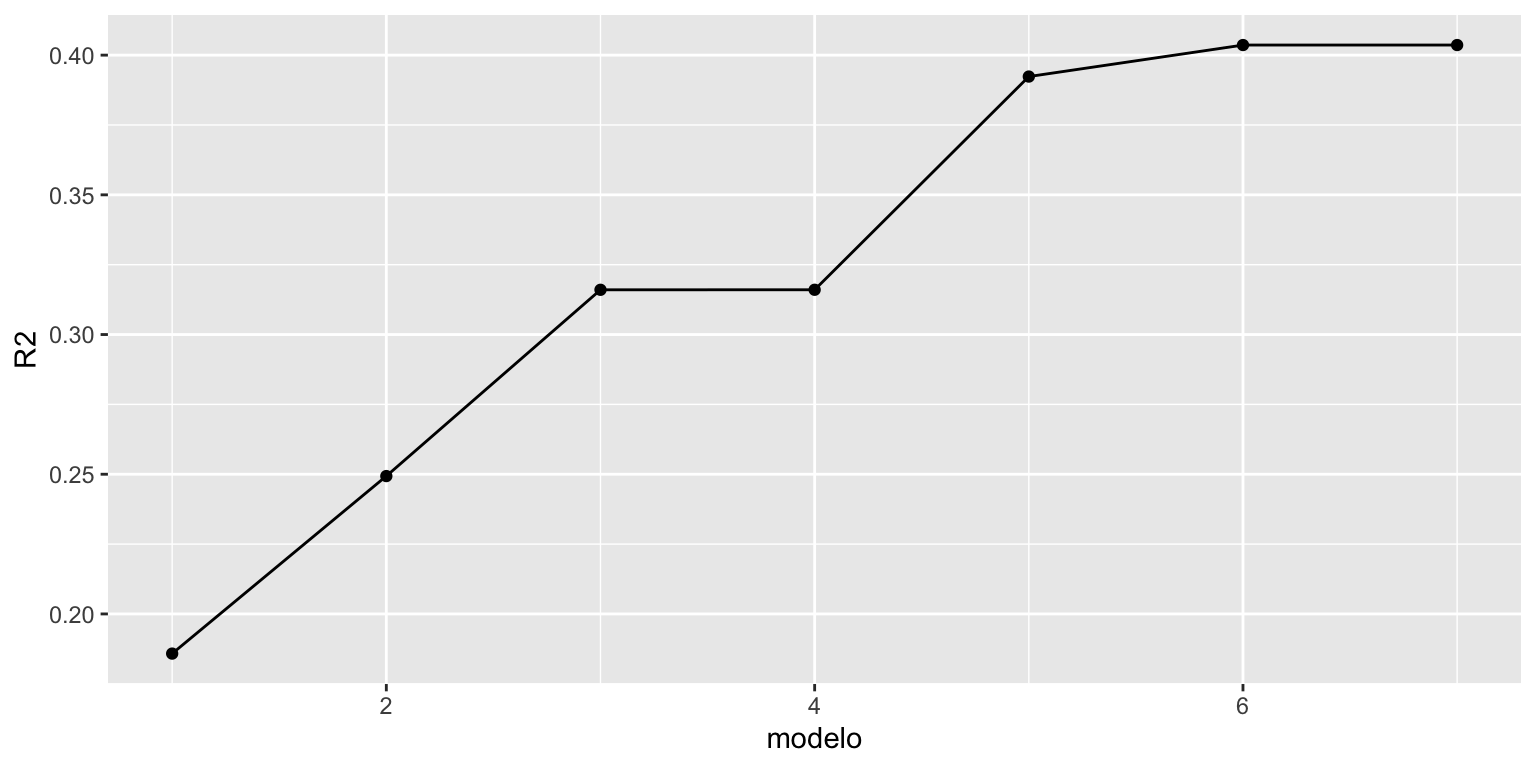 

R2

• Não é uma coincidência que \(R^2\) nunca tenha diminuido. De fato, \(R^2\) tem a desvantagem que nunca diminui quando incluímos uma nova variável no modelo (mesmo se a variável não for importante)
• Uma alternativa é usar uma nova medida de qualidade de ajuste.

\[R^2_{Adj} = 1 - \dfrac{n-1}{n-(k+1)} (1-R^2)\]

\(R^2_{Adj}\) penaliza o número de variáveis incluídas no modelo.

R2 ajustado

Code

modelo = 1:7
R2adj = c(summary(modelo1)$adj.r.squared, summary(modelo2)$adj.r.squared,
          summary(modelo3)$adj.r.squared, summary(modelo4)$adj.r.squared,
          summary(modelo5)$adj.r.squared, summary(modelo6)$adj.r.squared,
          summary(modelo7)$adj.r.squared)
dados = data.frame(R2adj, modelo)

library(ggplot2)
ggplot(dados, aes(y = R2adj, x = modelo)) + geom_line() +
  geom_point() + ylab("R2 ajustado")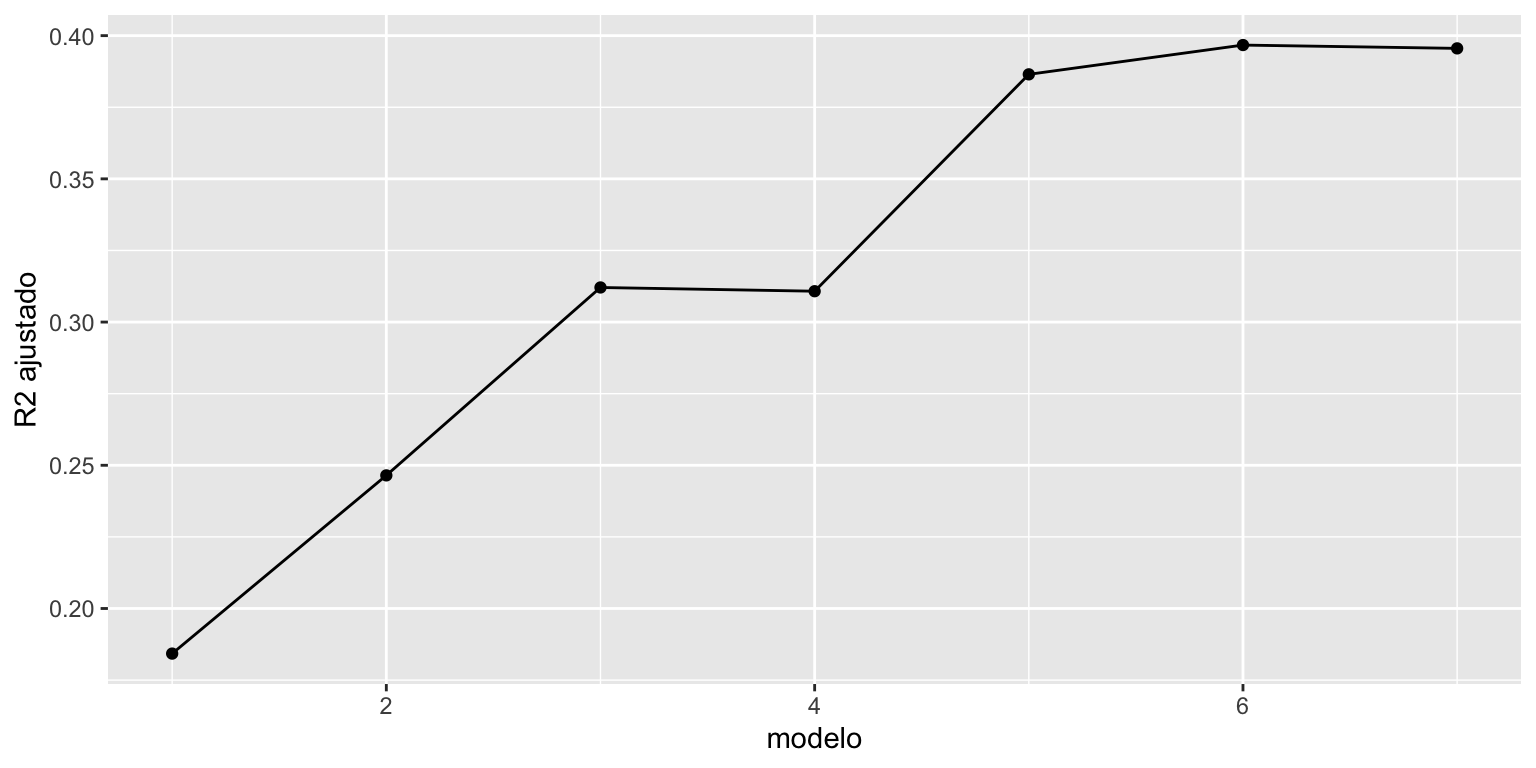

R2 ajustado

Comparando \(R^2\) com \(R^2-\)ajustado

Code

#R2
round(R2,4)

[1] 0.1858 0.2493 0.3160 0.3160 0.3923 0.4036 0.4036

Code

#R2-Ajustado
round(R2adj,4)

[1] 0.1843 0.2465 0.3121 0.3108 0.3865 0.3967 0.3956

\(R^2\) ou \(R^2_{Adj}\)? Prefere-se o \(R^2_{Adj}\).

\[R^2_{Adj} = 1 - \dfrac{n-1}{n-(k+1)}(1-R^2) = 1 - \dfrac{\hat{s}^2}{\tilde{\sigma}_y^2},\] em que \(\hat{s}^2\) e \(\tilde{\sigma}_y^2\) são estimadores não viesados para \(\sigma^2\) e \(\sigma_y^2\)

Qualidade de ajuste

• R
• Python
• Julia

Code

library(wooldridge)
modelo <- lm(wage ~ educ + tenure, data = wage1)
summary(modelo)$r.squared

[1] 0.301861

Code

summary(modelo)$adj.r.squared

[1] 0.2991912

Code

import wooldridge as woo
import statsmodels.formula.api as smf

wage1 = woo.dataWoo('wage1')
modelo = smf.ols(formula='wage ~ educ + tenure', data = wage1)
results = modelo.fit()
results.rsquared

0.30186096904683757

Code

results.rsquared_adj

0.29919122131852727

Code

using WooldridgeDatasets, DataFrames, GLM

wage1 = DataFrame(wooldridge("wage1"));
modelo = lm(@formula(wage ~ educ + tenure), wage1);
r2(modelo)

0.30186096904683746

Code

adjr2(modelo)

0.29919122131852716