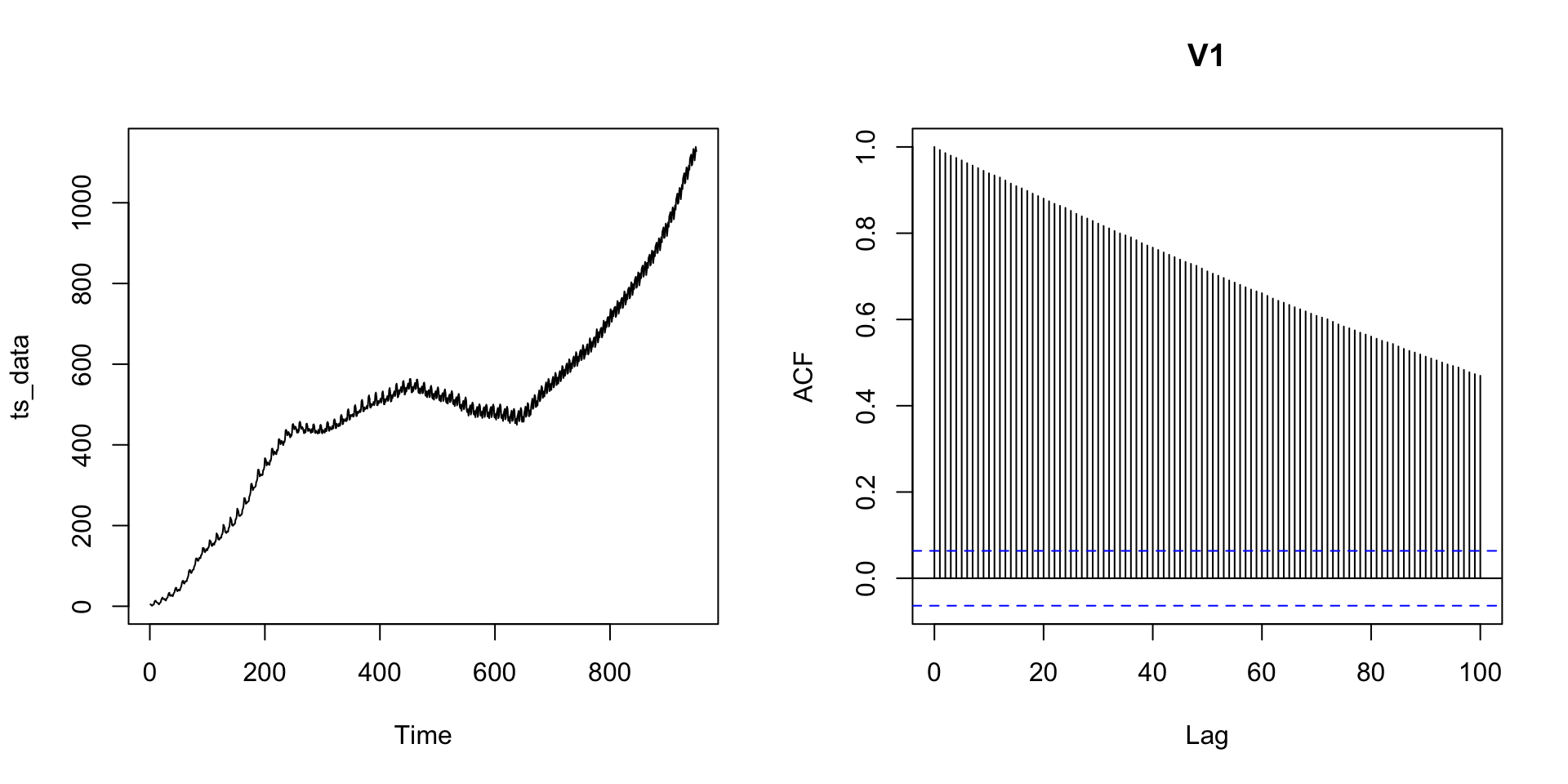
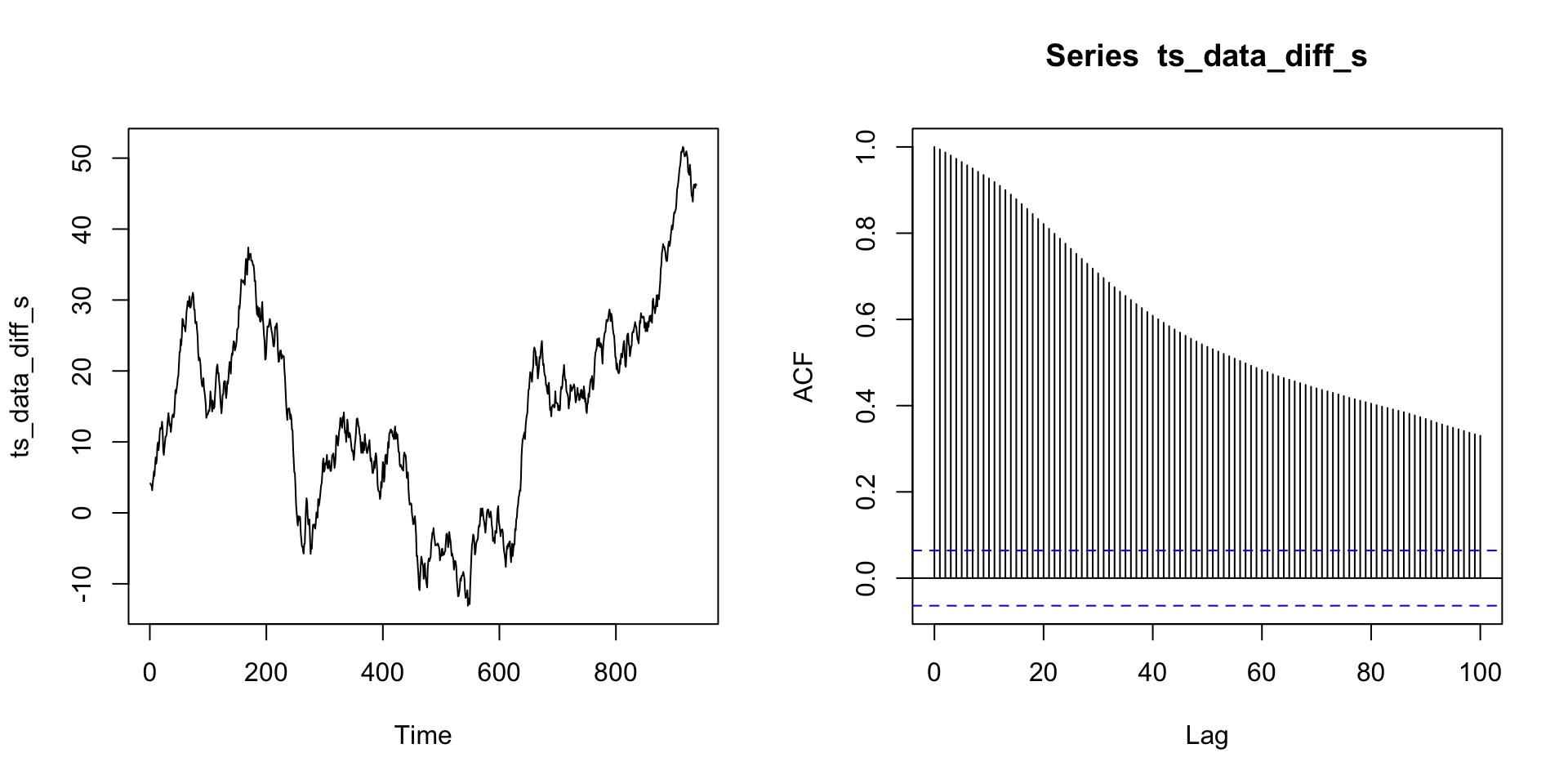
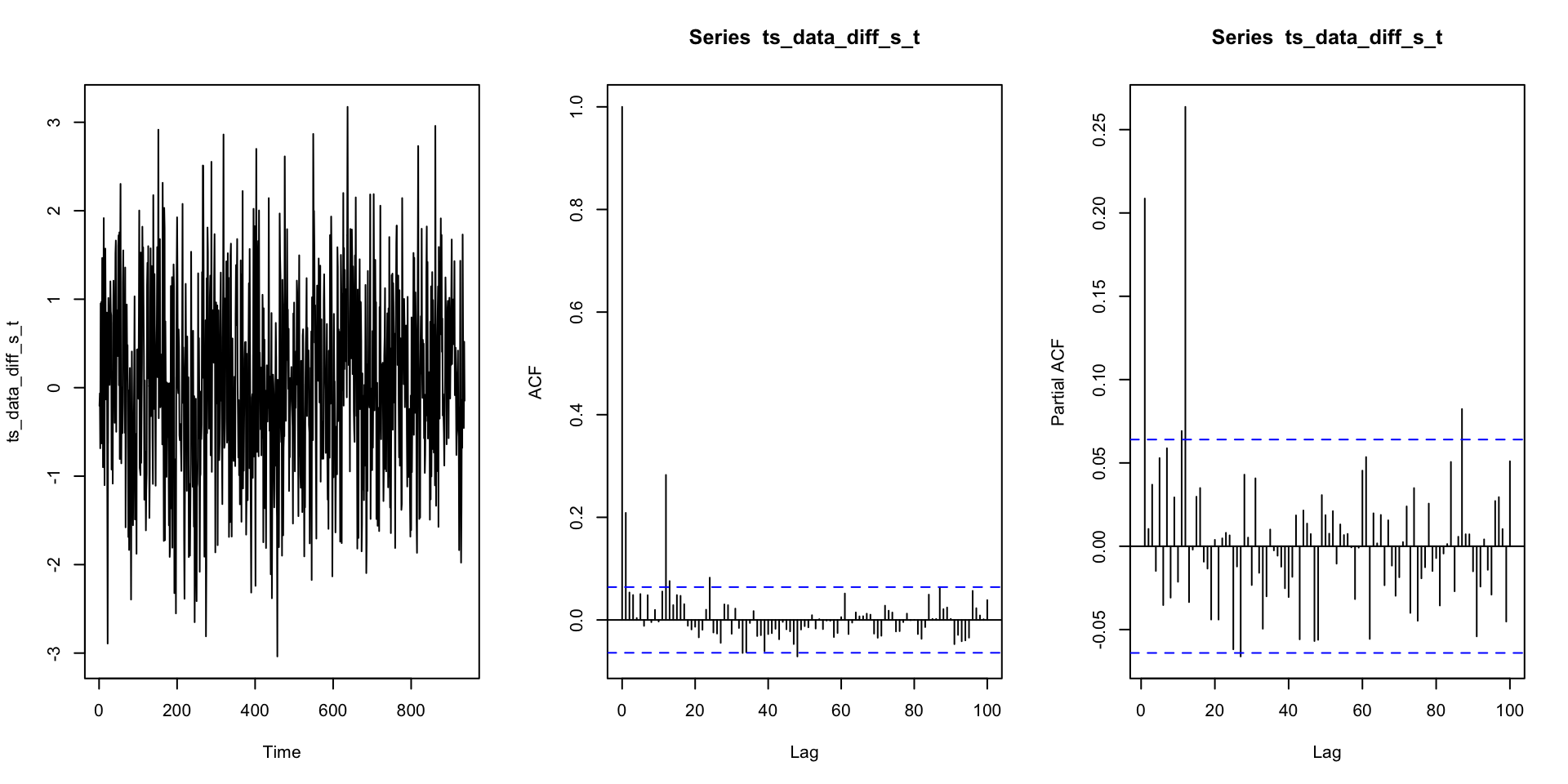
Rows: 950
Columns: 1
$ V1 <dbl> 4.587898, 4.165729, 2.003551, 1.347498, 3.484531, 3.766763, 4.62935…SARIMA
ME607 - Séries Temporais
ctrucios@unicamp.br
Instituto de Matemática, Estatística e Computação Científica (IMECC),
Universidade Estadual de Campinas (UNICAMP).
Introdução
Introdução
- Muitas séries temporais apresentam fenômenos sazonais que se repetem periodicamente.
- Esta sazonalidade é um tipo de falta de estacionariedade na média e é bastante frequente (Por exemplo, \(\mathbb{E}(Y_t) = \mathbb{E}(Y_{t+s})\)).
- Fenômenos sazonais pode ser produto de fatores climáticos, culturais, religiosos, etc. Exemplo:
- Formatura
- Mês das noivas
- Carnaval
- Natal
- Etc
- Como lidar com este tipo de dados?
Introdução
Métodos Tradicionais
\[Y_t = T_t + S_t + \epsilon_t\] - Métodos de decomposição - Modelos de regressão (tendência determinística + Dummy | Fourier)
SARIMA
ARIMA Sazonal
SARIMA
SARIMA
- Métodos tradicionais assumem que a componente sazonal é deterministica e independente das componentes não sazonais. Contudo, esta suposição não é tão realista assim.
- Muitas vezes \(S_t\) pode ser estocástica e correlacionada com as outras componentes. Nestes casos, extendemos ARIMA para também capturar a componente sazonal.
- Ou seja, \(\{Y_t\}\) terá uma relação dentro do período sazonal (\(\{Y_{t-1}, ..., Y_{t - s + 1}\}\)) e outra entre períodos (\(\{Y_{t-s}, Y_{t-2s}, ...\}\)).
- Assim como tentamos remover a tendência deterministica com diferebciação \(d\), tentamos remover a sazonalidade determinística com diferenciação sazinal \(D\) (\(Y_t - Y_{t - s}\)).
- Contudo, é possivel que mesmo após remover o comportamento sazonal determinístico, ainda exista correlação significativa em:
- Lags de ordem baixa: indicando que os resíduos ainda são correlacionados e um modelo ARMA poderia ajudar.
- Lags sazonais: indicando a necessidade de considerar sazonalidade estocástica (com modelos SARMA)
SARIMA
SARIMA
É possivel que, após diferenciação para remover a sazonalidade e a tendência, ainda existe correlação significativa em:
- lags de ordem baixa: indicando que os resíduos ainda são correlacionados e um modelo ARMA poderia ajudar a capturar a dinâmica dos dados.
- lags sazonais: indicando a necessidade de considerar sazonalidade estocástica, em cujo caso, modelo SARMA podem ajudar a capturar a dinâmica dos dados.
SARIMA
Definição:
Sejam \(d\) e \(D\) números inteiros não negativos (\(\mathbb{Z}_0^{+}\)), então \(\{y_t\}\) é um processo SARIMA \((p, d, q) \times (P, D, Q)_s\) (SARIMA com período sazonal \(s\)), se o processo \[z_t = (1 - B)^d (1 - B^s)^Dy_t\] é um processo ARMA definido por \[\phi(B) \Phi(B^s) z_t = \theta(B) \Theta(B^s) \epsilon_t, \quad \epsilon_t \sim RB(0, \sigma^2),\] em que
- \(\phi(B) = 1 - \phi_1B - \phi_2 B^2 - \cdots - \phi_p B^p\)
- \(\Phi(B^s) = 1 - \Phi_1B^s - \Phi_2 B^{2s} - \cdots - \Phi_P B^{Ps}\)
- \(\theta(B) = 1 + \theta_1B + \theta_2 B^2 + \cdots + \theta_q B^q\)
- \(\Theta(B) = 1 + \Theta_1B^s + \Theta_2 B^{2s} + \cdots + \Theta_Q B^{Qs}\)
Observação: na prática \(D \leq 1\) e \(P, Q < 3\).
SARIMA
Note que o modelo SARIMA definido anteriormente pode ser reescrito como \[\phi^{\ast}(B) z_t = \theta^{\ast}(B) \epsilon_t,\]
em que:
- \(\phi^{\ast}(B)\) é um polinômio de grau p + Ps.
- \(\theta^{\ast}(B)\) é um polinômio de grau q + Qs.
Exemplos
- SARIMA \((1, 0, 1) \times (1, 0, 1)_12\)
- SARIMA \((1, 0, 2) \times (2, 0, 1)_7\)
- Etc.
SARIMA
Suponha que temos \(r\) anos de dados mensais:
| Ano Mês | Jan | Fev | Mar | … | Dez |
|---|---|---|---|---|---|
| 1 | \(y_1\) | \(y_2\) | \(y_3\) | …. | \(y_{12}\) |
| 2 | \(y_{13}\) | \(y_{14}\) | \(y_{15}\) | …. | \(y_{24}\) |
| \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) | …. | \(\vdots\) |
| r | \(y_{1 + 12(r-1)}\) | \(y_{2 + 12(r-1)}\) | \(y_{3 + 12(r-1)}\) | …. | \(y_{12 + 12(r-1)}\) |
SARIMA
- Cada coluna pode ser vista como a realização de uma série temporal.
- Assumamos que cada coluna é gerada pelo mesmo processo ARMA(P, Q).
- Ou seja, para cada coluna \(j = 1, \cdots, 12\) temos \[\begin{align} y_{j + 12t} &= \Phi_1 y_{j + 12(t - 1)} + \cdots + \Phi_P y_{j + 12(t-P)} \notag \\ &\quad + U_{j + 12t} + \Theta_1 U_{j + 12(t - 1)} + \cdots + \Theta_Q U_{j + 12(t - Q)}, \end{align}\] em que \(U_{j + 12t} \sim RB(0, \sigma^2_U)\).
- Note que \(\mathbb{E}(U_t U_{t+h})\) não necessariamente é zero (exceto de \(h\) for múltiplo do período sazonal).
SARIMA
\[\Phi(B^{12})y_t = \Theta(B^{12})U_t\]
- Se \(Q = 1\), \(P = 0\) e \(\Theta_1 = -0.4\), então para as séries de cada mês em particular temos um \(MA(1)\).
- Se ademais \(\mathbb{E}(U_t U_{t+h}) = 0\), \(\forall h\) (ou seja, se as sequências para diferentes meses são não correlacionados entre si), então as colunas são não correlacionadas e a ACF seria da forma:
SARIMA
\[\Phi(B^{12})y_t = \Theta(B^{12})U_t\]
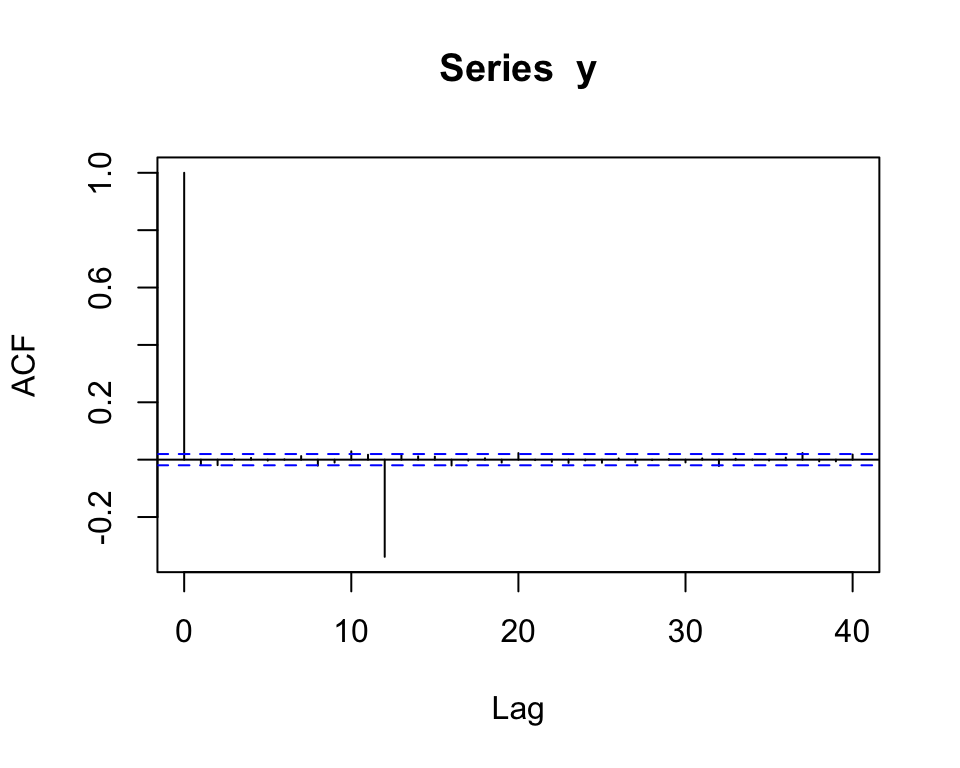
- Se \(Q = 1\), \(P = 0\) e \(\Theta_1 = -0.4\), então para as séries de cada mês em particular temos um \(MA(1)\).
- Se ademais \(\mathbb{E}(U_t U_{t+h}) = 0\), \(\forall h\) (ou seja, se as sequências para diferentes meses são não correlacionados entre si), então as colunas são não correlacionadas e a ACF seria da forma:
SARIMA
\[\Phi(B^{12})y_t = \Theta(B^{12})U_t\]
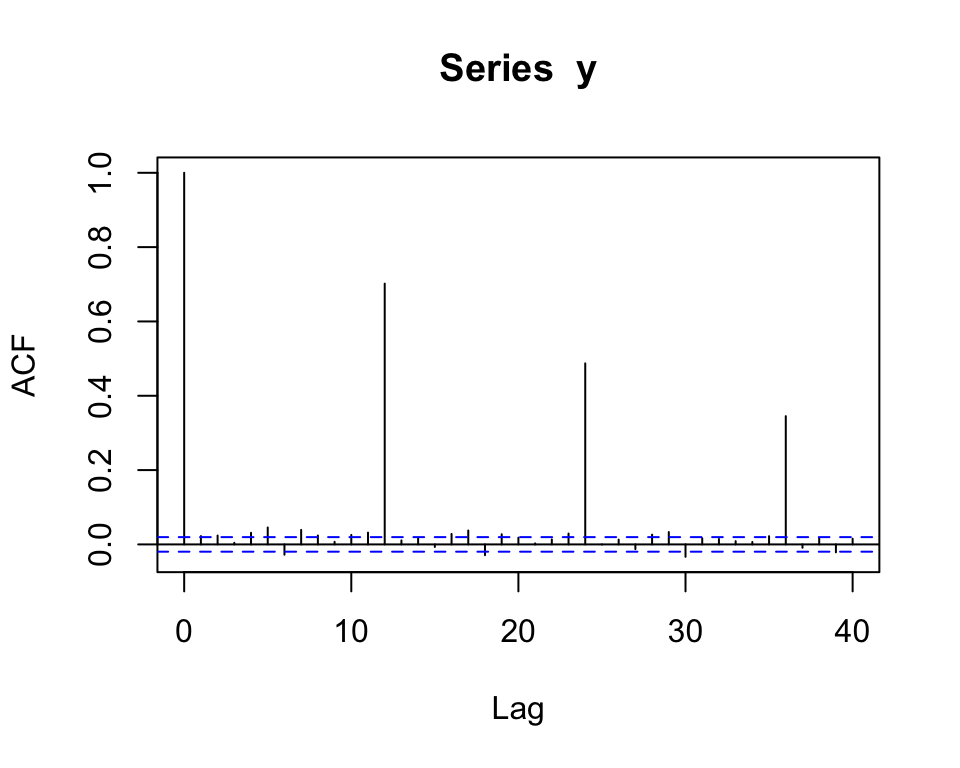
- Se \(Q = 0\), \(P = 1\) e \(\Phi_1 = 0.7\), então para as séries de cada mês em particular temos um \(AR(1)\).
- Se ademais \(\mathbb{E}(U_t U_{t+h}) = 0\), \(\forall h\) (ou seja, se as sequências para diferentes meses são não correlacionados entre si), então as colunas são não correlacionadas e a ACF seria da forma:
SARIMA
- Nos modelos dos exemplos anteriores (assumindo \(\mathbb{E}(U_t U_{t+h}) = 0\) \(\forall h\)), as 12 séries (correspondentes a cada mês) são não correlacionados.
- Para incorporar dependência entre as séries permitimos que \(\{U_t\} \sim ARMA(p, q)\), \[\phi(B)U_t = \theta(B)\epsilon_t, \quad \epsilon_t \sim RB(0, \sigma^2_{\epsilon})\]
- Isto implica possíveis correlações não apenas entre \(U_t\) consecutivos, mas também nas sequências sazonais
- Ou seja, a suposição \(U_{j + 12t} \sim RB(0, \sigma^2_U)\) não esta mais valendo (embora na prática \(\mathbb{E}(U_tU_{t + 12j})\) é pequeno).
- Misturando ambos os modelos, temos exatamente o modelo definido na definição do modelo SARIMA! 🏄♀️
SARIMA
\[\Phi(B^{12})y_t = \Theta(B^{12})U_t\]
\[\phi(B)U_t = \theta(B)\epsilon_t\]
Substituindo \(U_t\) temos
\[\Phi(B^{12})y_t = \Theta(B^{12}) \dfrac{\theta(B)}{\phi(B)}\epsilon_t\]
O que implica em
\[\phi(B) \Phi(B^{12})y_t = \Theta(B^{12}) \theta(B) \epsilon_t\]
Identificação
Identificação
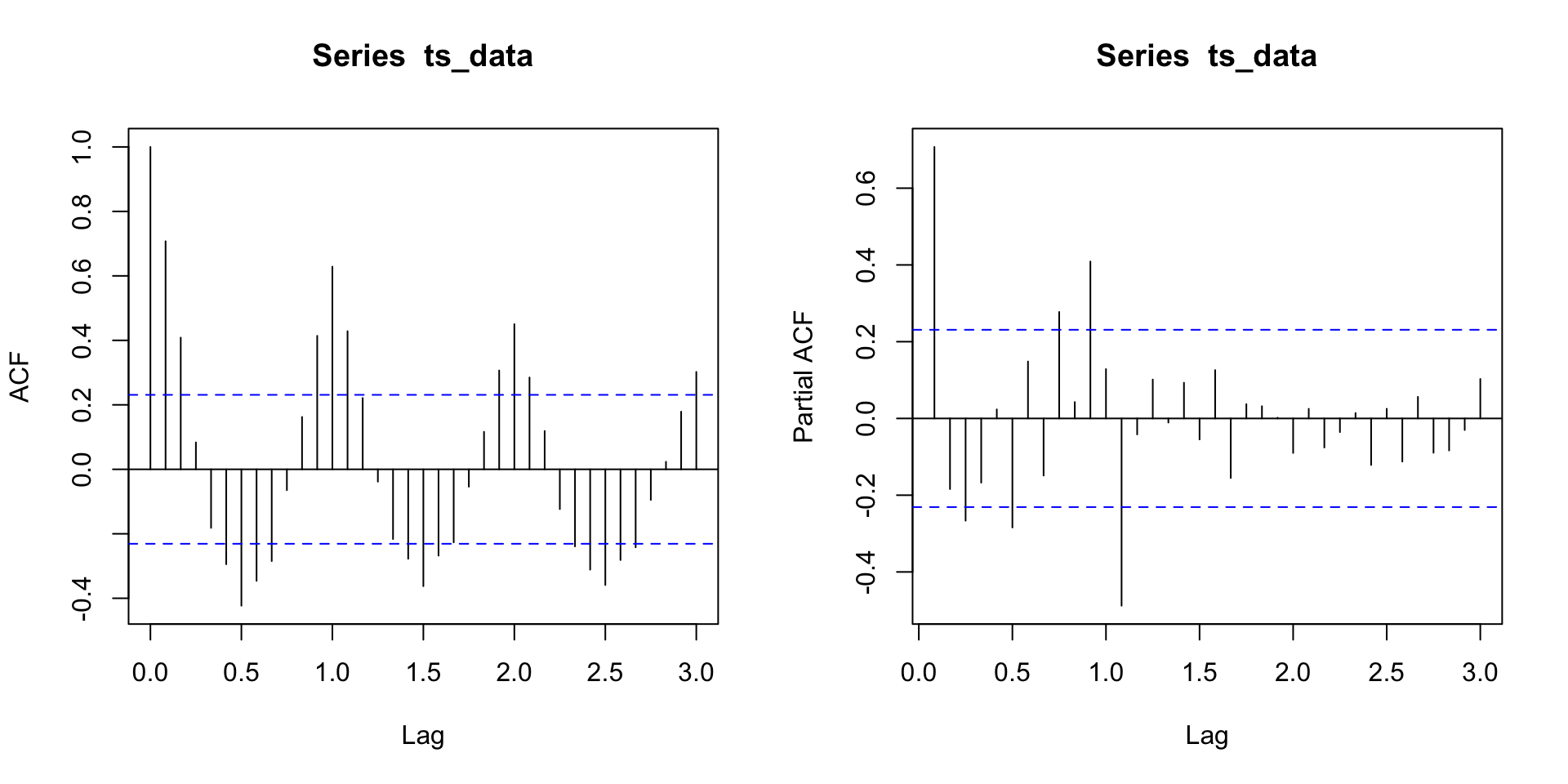
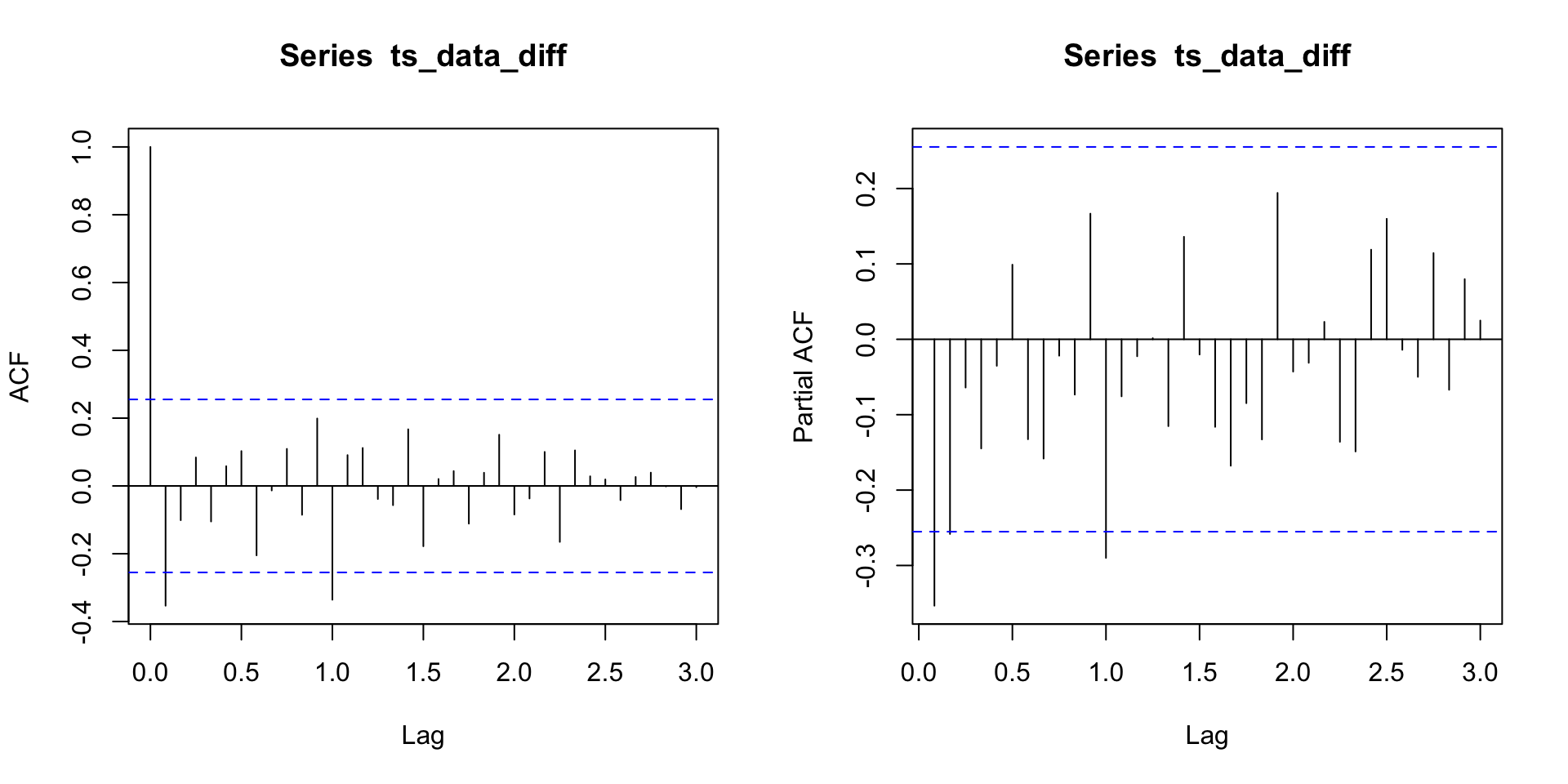
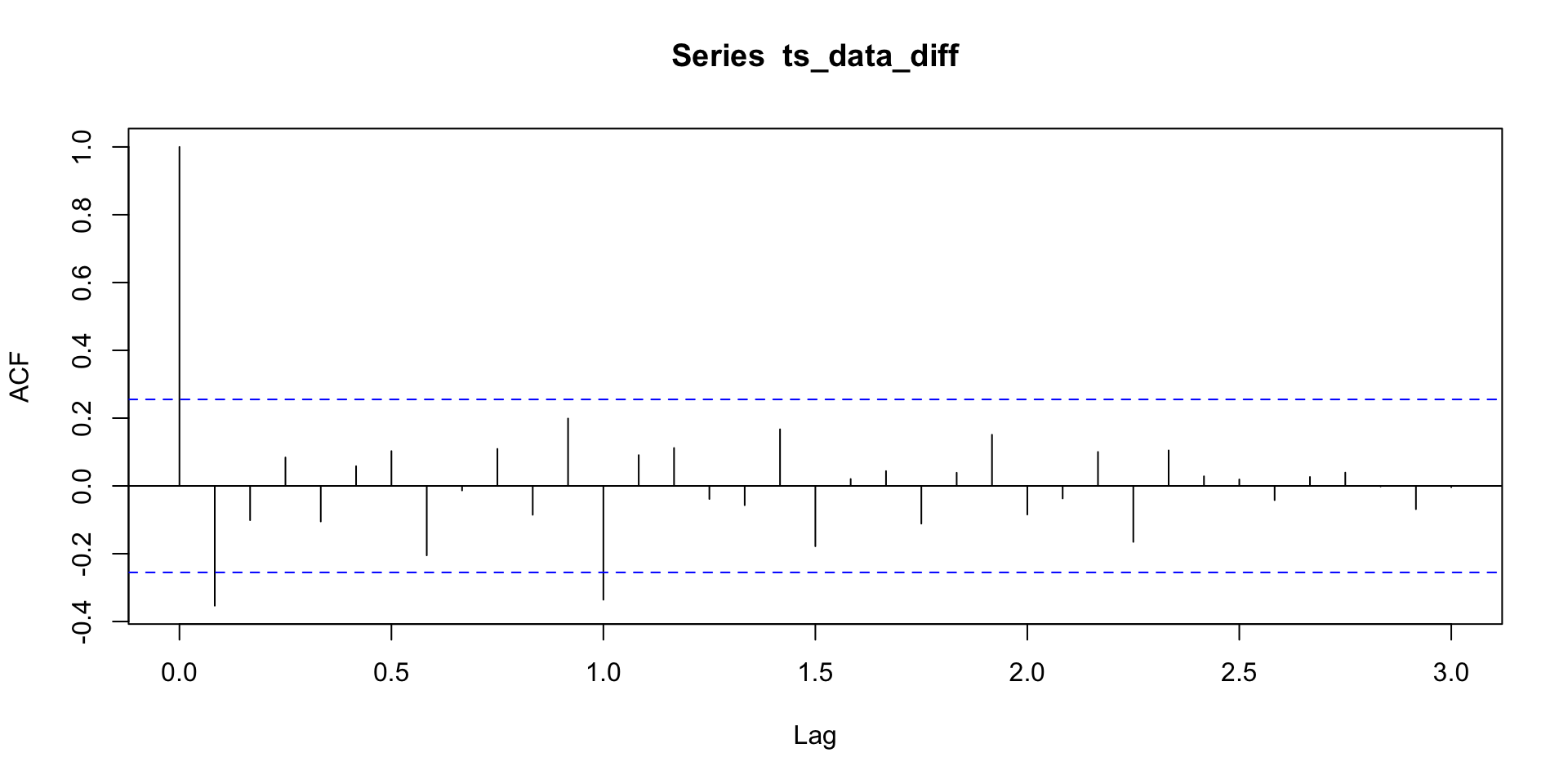
- Eencontrar \(d\) e \(D\) para diferenciar a série original para que seja aparentemente estacionária, \[Y_t = (1 - B)^d (1 - B^s)^D X_t.\]
- Calcular ACF e PACF de \(\{Y_t\}\) e identificar \(p\), \(q\), \(P\) e \(Q\) (de forma análoga ao feito em processos ARMA).
- Se \(\hat{\rho}(\cdot)\) são as autocorrelações de \(\{Y_t\}\), \(P\) e \(Q\) devem ser escolhidos de forma que \(\hat{\rho}(ks)\) (\(k = 1, 2, 3, ...\)) sejam compativeis com um ARMA(P, Q).
- \(p\) e \(q\) são escolhidos de forma que \(\hat{\rho}(1), \cdots, \hat{\rho}(s - 1)\) sejam compatíveis com um ARMA(p, q).
- Se tiver vários candidatos para a ordem do modelo, pode utilizar um critério (como AICc, BIC, etc).
- Ajustar o modelo por ML. Note que \(Y_t = (1 - B)^d (1 - B^s)^D X_t\) é um ARMA(p + sP, q + sQ) em que alguns coeficientes são zeros (além de outras restrições no modelo).
Exemplos
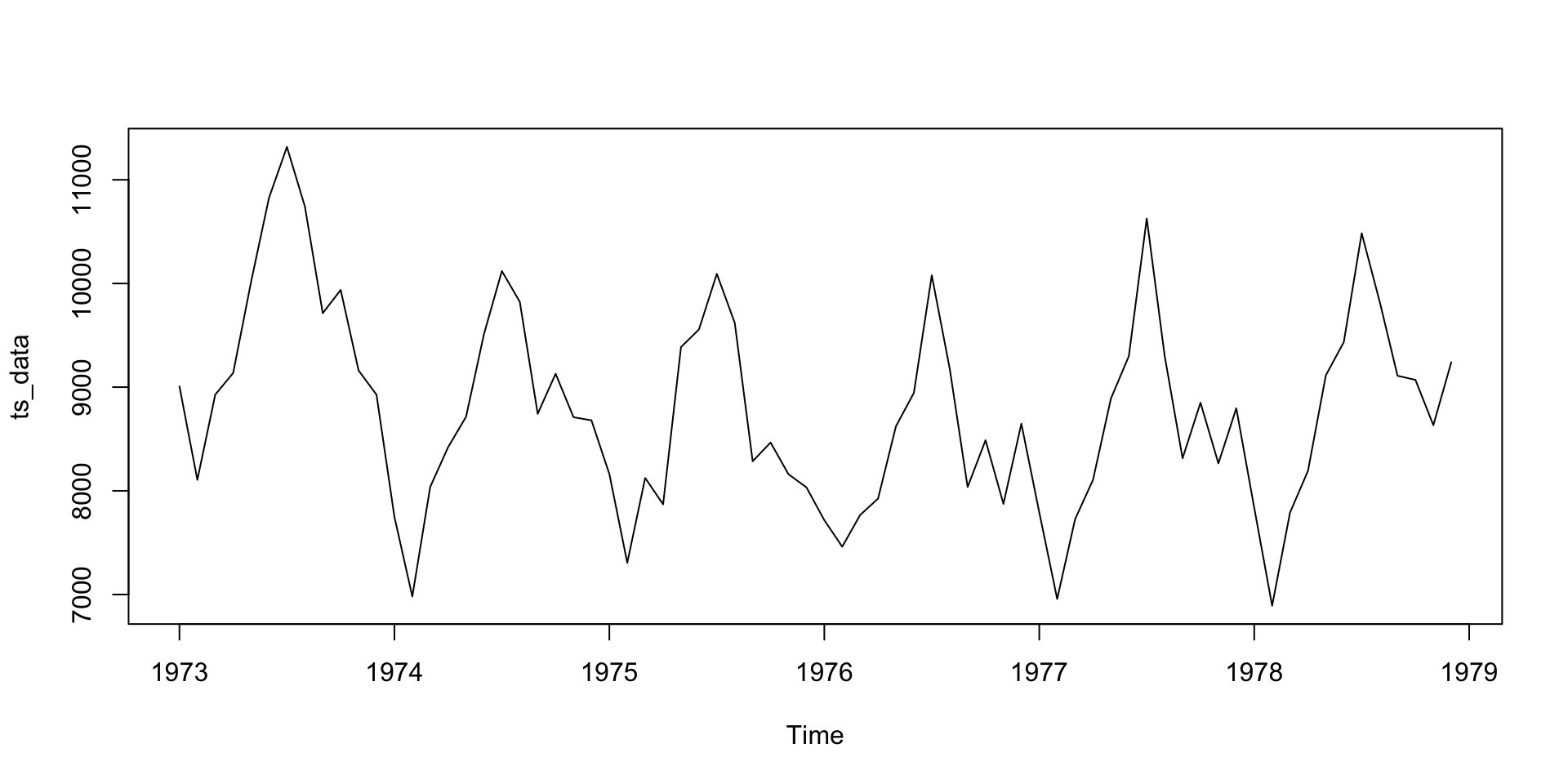
Mortes (mensais) acidentais US entre 1973 e 1978.
Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
1973 9007 8106 8928 9137 10017 10826 11317 10744 9713 9938 9161 8927
1974 7750 6981 8038 8422 8714 9512 10120 9823 8743 9129 8710 8680
1975 8162 7306 8124 7870 9387 9556 10093 9620 8285 8466 8160 8034
1976 7717 7461 7767 7925 8623 8945 10078 9179 8037 8488 7874 8647
1977 7792 6957 7726 8106 8890 9299 10625 9302 8314 8850 8265 8796
1978 7836 6892 7791 8192 9115 9434 10484 9827 9110 9070 8633 9240SARIMA \((0, 1, 1) \times (0, 1, 1)_{12}\)
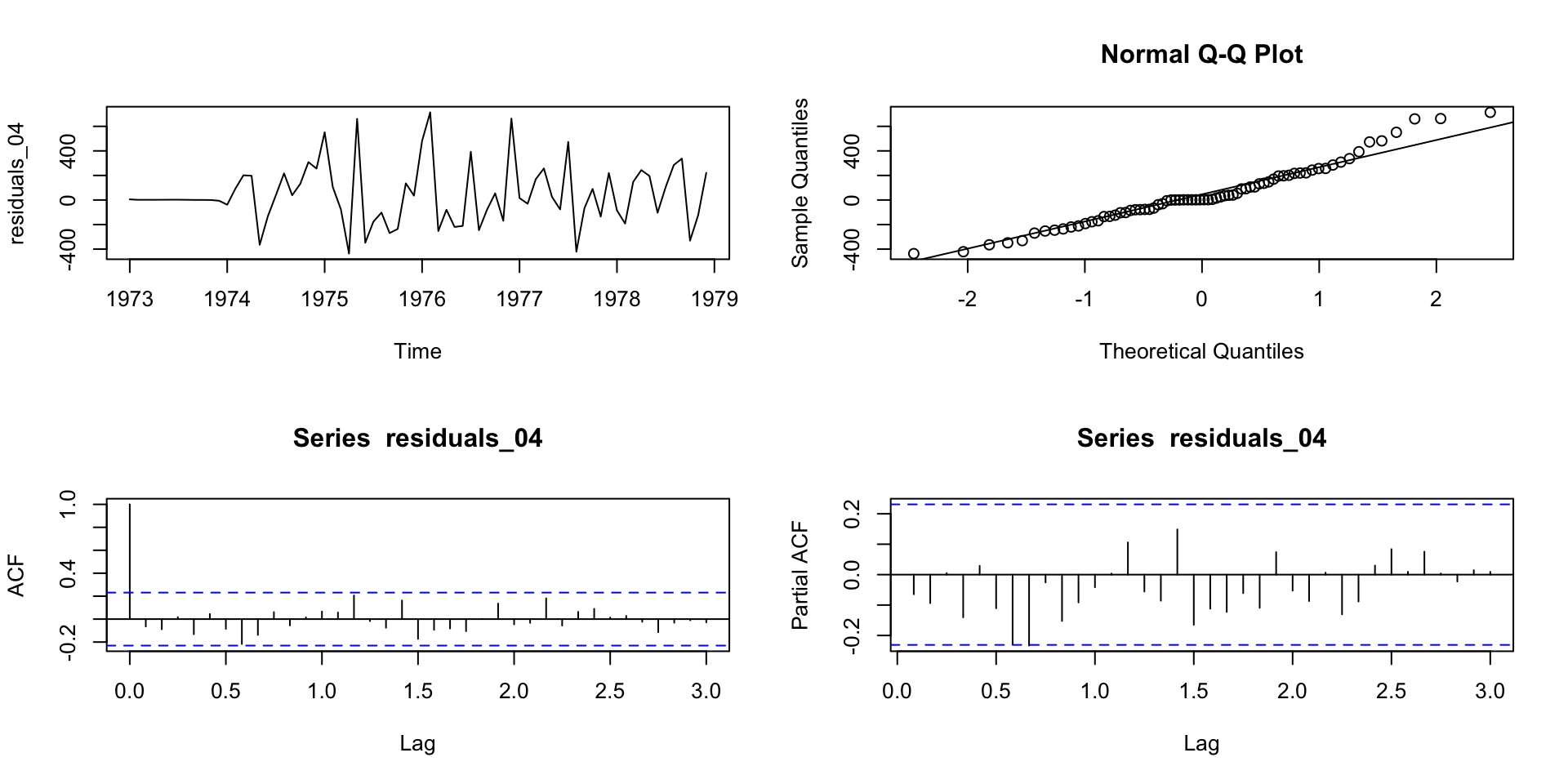
Mortes (mensais) acidentais US entre 1973 e 1978.
- E se eu não tiver certeza que \(p = 0\), \(q = 1\), \(P = 1\) e \(Q = 1\)?
- Um SARIMA \((0, 1, 1) \times (0, 1, 1)_{12}\) é um \(MA(q + sQ) = MA(13)\) com restrição, né? Então, porque não ajustar um \(MA(13)\)?
- Observação: como temos poucos dados, utilizaremos apenas métricas dentro da amostra. Se tivéssemos muitos dados, poderiamos fazer um rolling window e ver qual faz melhor previsão.
Code
[1] 873.7457 868.4179 864.6874 866.6413 868.4728 863.6197 860.2355 862.2132
[9] 864.3034 859.6358 857.2329 859.3756 865.4692 860.9361 858.6464 860.8906[1] 11 p q P Q
1 0 0 0 0
2 1 0 0 0
3 0 1 0 0
4 1 1 0 0
5 0 0 1 0
6 1 0 1 0
7 0 1 1 0
8 1 1 1 0
9 0 0 0 1
10 1 0 0 1
11 0 1 0 1
12 1 1 0 1
13 0 0 1 1
14 1 0 1 1
15 0 1 1 1
16 1 1 1 1
Call:
arima(x = ts_data, order = c(0, 1, 13), seasonal = c(0, 1, 0))
Coefficients:
ma1 ma2 ma3 ma4 ma5 ma6 ma7 ma8
-0.4166 0.0947 -0.0592 -0.0707 0.2439 -0.2881 -0.0624 -0.0233
s.e. 0.1582 0.2072 0.2264 0.2523 0.2284 0.2367 0.1660 0.2157
ma9 ma10 ma11 ma12 ma13
0.0514 0.1455 0.0458 -0.6686 0.3867
s.e. 0.2193 0.2428 0.2182 0.2289 0.2123
sigma^2 estimated as 79206: log likelihood = -421.76, aic = 871.52. . .
Code
Call:
arima(x = ts_data, order = c(0, 1, 13), seasonal = c(0, 1, 0), fixed = c(NA,
0, 0, 0, NA, NA, 0, 0, 0, 0, 0, NA, NA))
Coefficients:
ma1 ma2 ma3 ma4 ma5 ma6 ma7 ma8 ma9 ma10 ma11
-0.5018 0 0 0 0.2604 -0.2209 0 0 0 0 0
s.e. 0.2074 0 0 0 0.1703 0.1890 0 0 0 0 0
ma12 ma13
-0.9289 0.2032
s.e. 0.2492 0.1830
sigma^2 estimated as 66822: log likelihood = -422.64, aic = 857.27Code
Call:
arima(x = ts_data, order = c(0, 1, 13), seasonal = c(0, 1, 0), fixed = c(NA,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, NA, NA))
Coefficients:
ma1 ma2 ma3 ma4 ma5 ma6 ma7 ma8 ma9 ma10 ma11 ma12
-0.5180 0 0 0 0 0 0 0 0 0 0 -0.8833
s.e. 0.2235 0 0 0 0 0 0 0 0 0 0 0.3295
ma13
0.1323
s.e. 0.2018
sigma^2 estimated as 75607: log likelihood = -424.92, aic = 857.83[1] 857.2329 878.8892 864.6387 865.2017Seleção de Modelos
Seleção de Modelos
- Como visto anteriormente, algumas vezes vários modelos podem capturar razoavelmente bem a dinâmica dos dados e precisamos escolher o melhor modelo (o modelo que irá para produção).
- Esta escolha não sempre é fácil.
- Alguns métodos que nos ajudam neste escolha são:
- Validação cruzada para séries temporais
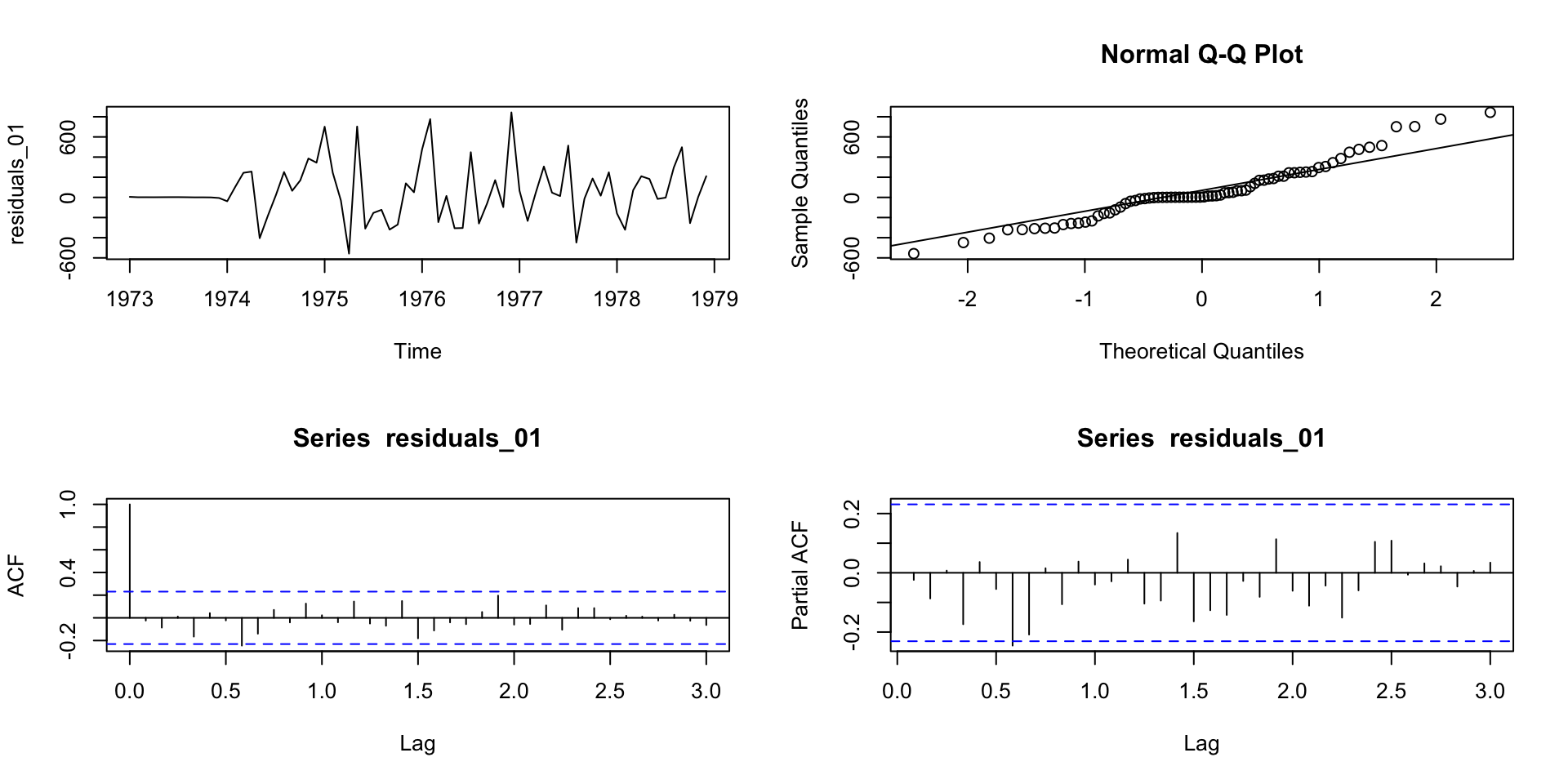
- Estatísticas dos resíduos (in-sample)
- Critérios de informação.
Seleção de Modelos
Seja \(k\) o número de parâmetros estimados e \(n\) o tamanho da série:
\[AIC = -2 \log(\underbrace{\text{máxima verossimilhança}}_{L}) + 2k\]
\[\log L = -\frac{n}{2} \log (2 \pi \sigma^2_{\epsilon}) - \dfrac{1}{2\sigma^2_{\epsilon}} S(\boldsymbol{\Theta}, y)\]
Maximizando, obtemos \(\hat{\boldsymbol{\Theta}}\) e então \(\log \hat{L}\),
\[\log \hat{L} = \underbrace{-\frac{n}{2} \log (2 \pi \hat{\sigma}^2_{\epsilon})}_{-\dfrac{n}{2} \log(2\pi) - \dfrac{n}{2} \log (\hat{\sigma}^2_{\epsilon})} - \underbrace{\dfrac{1}{2\hat{\sigma}^2_{\epsilon}} n \hat{\sigma}^2_{\epsilon}}_{\dfrac{n}{2}}\]
Seleção de Modelos
\[AIC = n \log(\hat{\sigma}^2_{\epsilon}) + 2k\]- AIC superestima a ordem do modelo
- Outros critérios foram desenvolvidos:
- BIC
- AICc
- Shibata (SBC)*
- Hannan-Quinn
- Etc.
- A regra geral é, quanto menor, melhor!
Seleção de Modelos
| Critério | Fórmula | Penalização | Objetivo / Comentário |
|---|---|---|---|
| AIC | ( = -2 L + 2k ) | Linear | Equilíbrio entre ajuste e complexidade |
| AICc | ( = + ) | Corrige o AIC | Corrige o AIC para amostras pequenas |
| BIC (Schwarz) | ( = -2 L + k n ) | Logarítmica | Favorece modelos mais simples |
| HQ (Hannan-Quinn) | ( = -2 L + 2k (n) ) | Intermediária | Penalização entre AIC e BIC |
| Shibata (SBC) | Semelhante ao AIC, recomendado para previsão | Similar ao AIC | Melhor desempenho preditivo em alguns contextos |
Seleção de Modelos
- Shibata (1976) mostrou que o uso da mesma fórmula do AIC, com foco em previsão out-of-sample, é assintoticamente eficiente: ou seja, mesmo quando o modelo verdadeiro não pertence à classe considerada (por exemplo, um ARMA aproximando uma série mais complexa), essa fórmula ainda tende a selecionar o modelo com melhor desempenho preditivo à medida que \(n \rightarrow \infty\).
- A AICc é útil para selecionar entre modelos dentro da mesma classe. Por exemplo, podemos usá-la para escolher um modelo ARIMA entre modelos ARIMA candidatos. O mesmo aplica para outros critérios de informação.
- Critérios de informação apenas são úties para compara modelos com as mesmas ordens de diferenciação.
Referências
- Brockwell, P. J., & Davis, R. A. (Third Edition). (2016). Introduction to Time Series and Forecasting. New York, NY: Springer New York.. Chapter 8
- Hyndman, R.J., & Athanasopoulos, G. (2021). Forecasting: principles and practice, 3rd edition, OTexts: Melbourne, Australia. OTexts.com/fpp3.. Chapter 9.
- Shibata, R. (1976). Selection of the order of an autoregressive model by Akaike’s Information Criterion. Biometrika, 63(1), 117–126.
- Peña, D. (2010). Análisis de Series Temporales. Cap 7.

Carlos Trucíos (IMECC/UNICAMP) | ME607 - Séries Temporais | ctruciosm.github.io