Processos de Médias Móveis - MA(q)

ME607 - Séries Temporais

Prof. Carlos Trucíos
ctrucios@unicamp.br

Instituto de Matemática, Estatística e Computação Científica (IMECC),
Universidade Estadual de Campinas (UNICAMP).

MA(1)

MA(1)

Definição:

Um processo estocástico \(\{Y_t\}\) é dito de médias móveis de ordem 1, denotado MA(1), se seu processo gerador de dados é dado por \[Y_t = \mu + \epsilon_t + \theta \epsilon_{t-1},\] em que \(\mu\) e \(\theta \text{ } (\theta \neq 0)\) são parâmetros reais e \(\epsilon_t \sim RB(0, \sigma^2_{\epsilon})\).

  • \(\mathbb{E}(Y_t) = \mu\)
  • \(\mathbb{V}(Y_t) = (1 + \theta^2) \sigma^2_{\epsilon}\)
  • \(\mathbb{C}ov(Y_t, Y_{t-1}) = \sigma^2_{\epsilon} \theta\)
  • \(\mathbb{C}ov(Y_t, Y_{t-k}) = 0, \quad k \geq 2\)

A média é constante, a variância é constante e a covariância não depende de \(t\). Ou seja, o processo é estacionário.

MA(1)

MA(1)

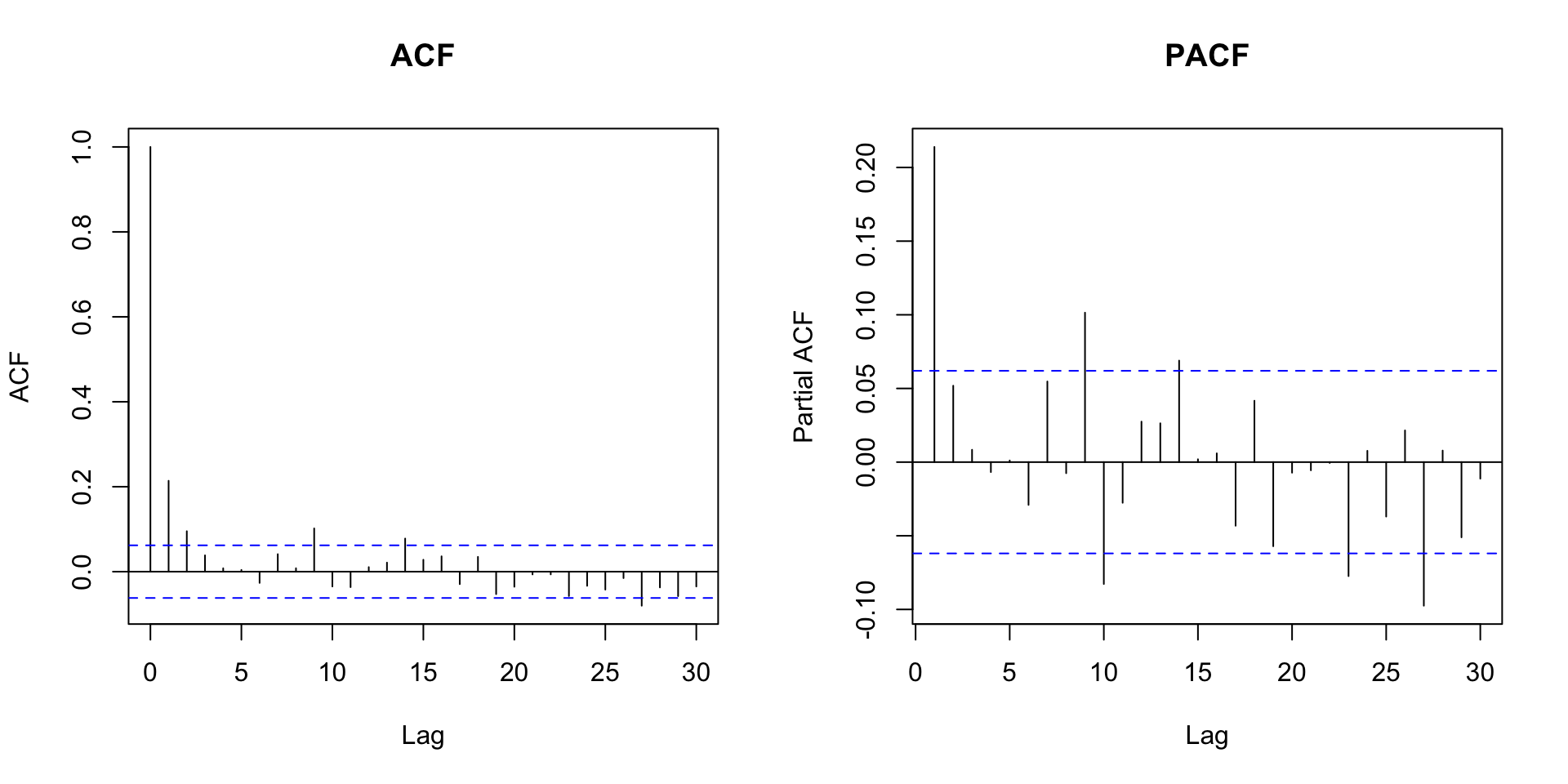
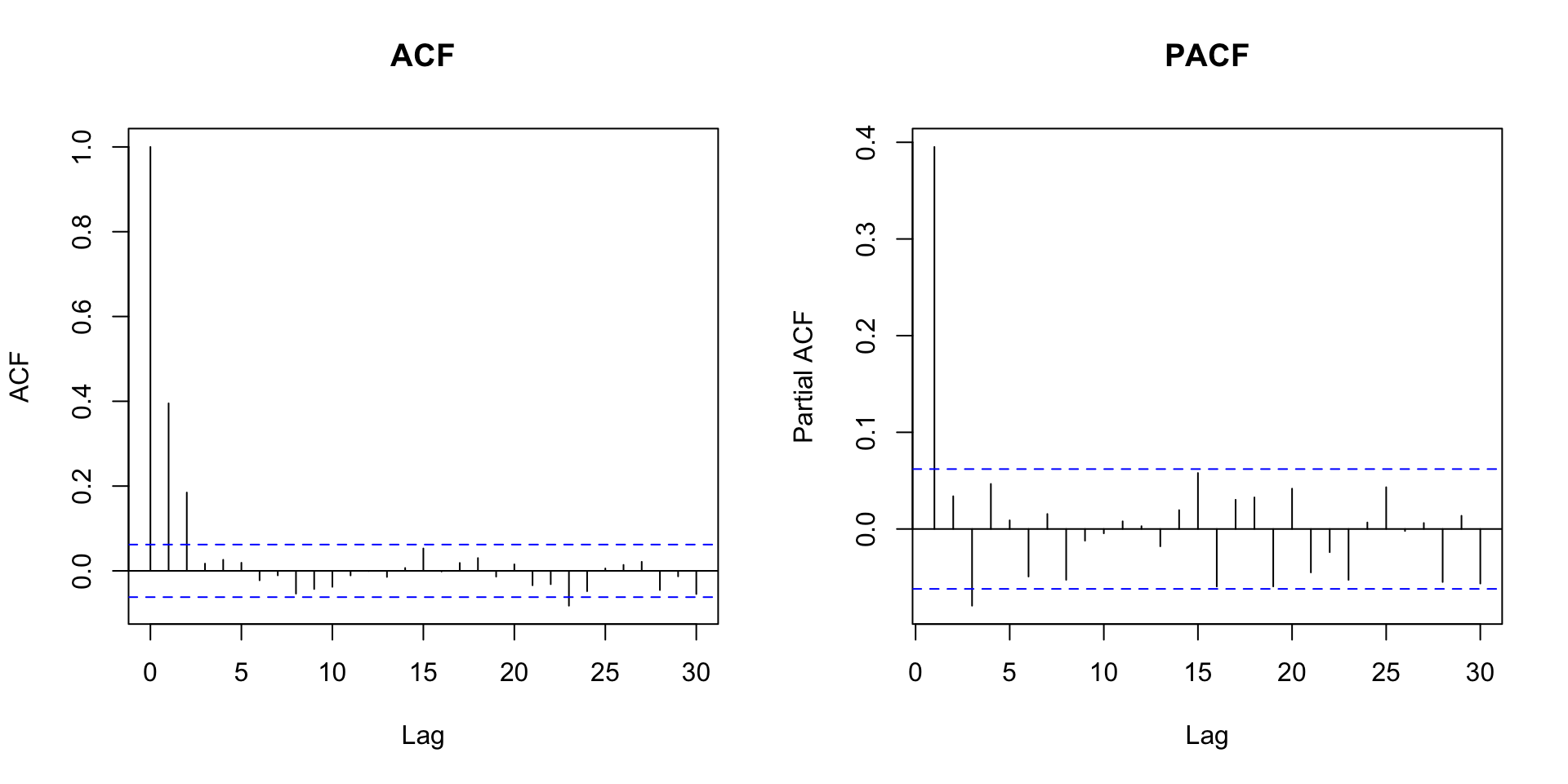
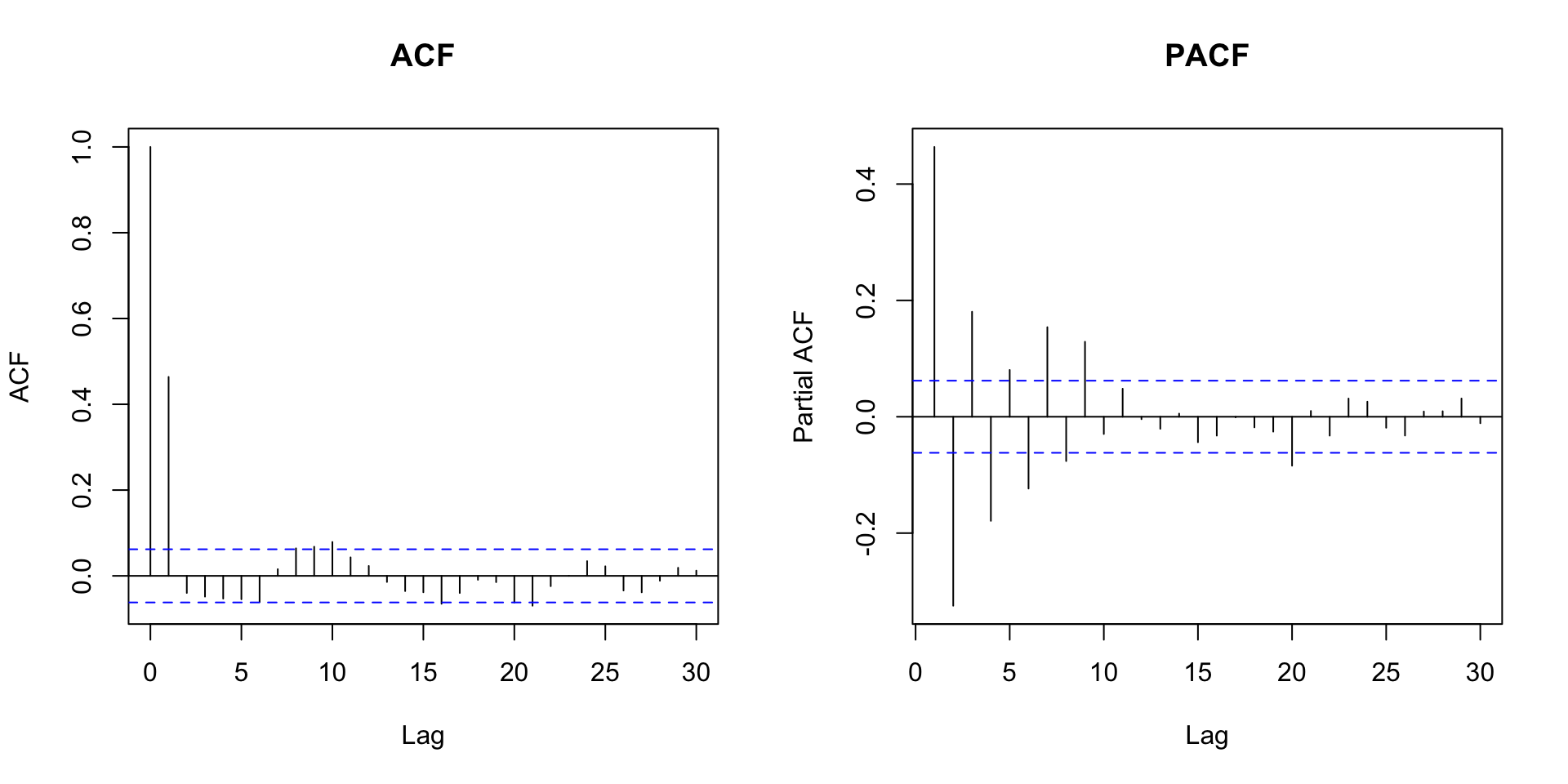
Função de autocorrelação

É facil verificar que:

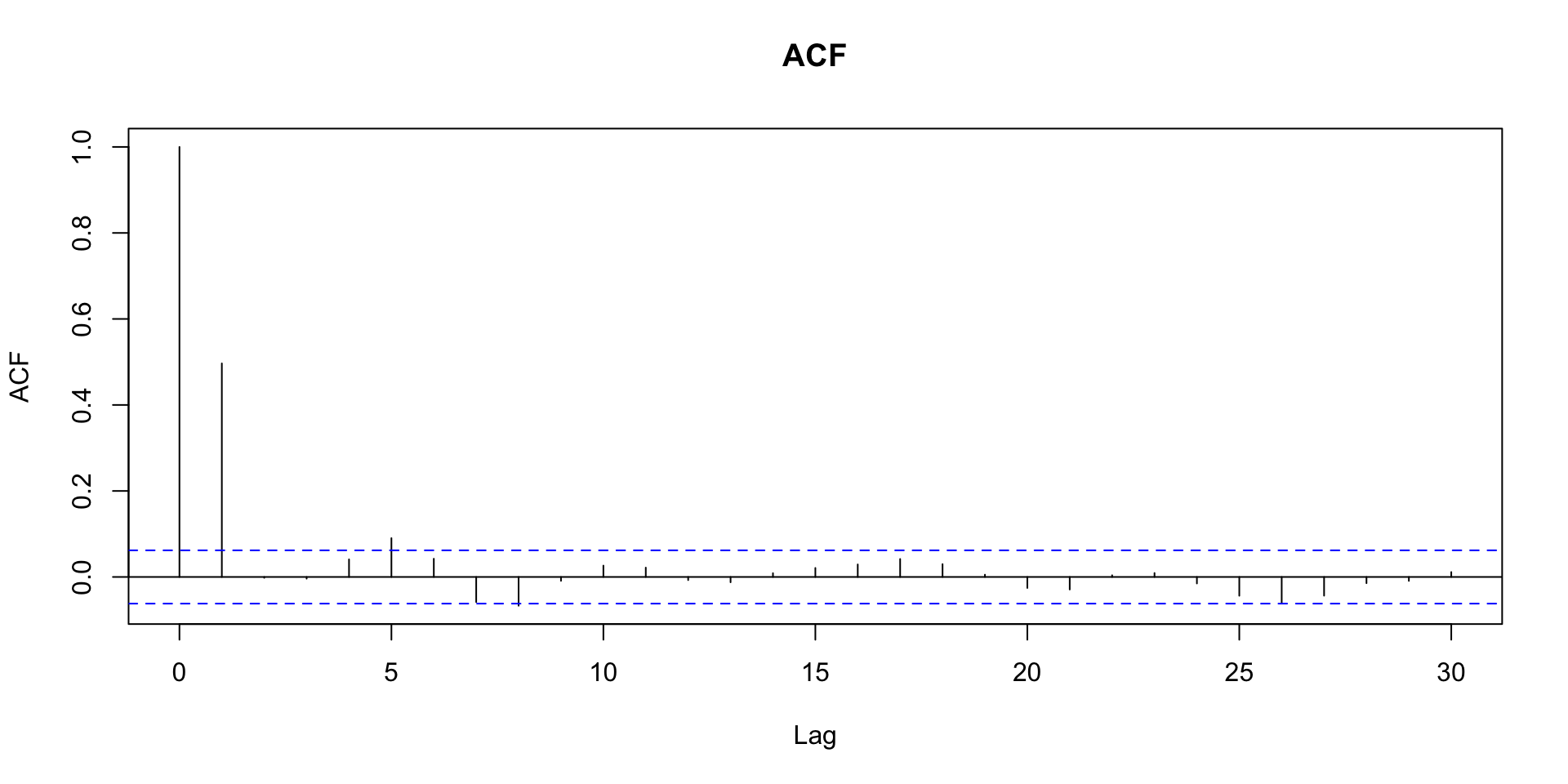
\[\rho_1 = \dfrac{\theta}{1 + \theta^2},\]

\(k \geq 2\) \[\rho_k = 0.\]

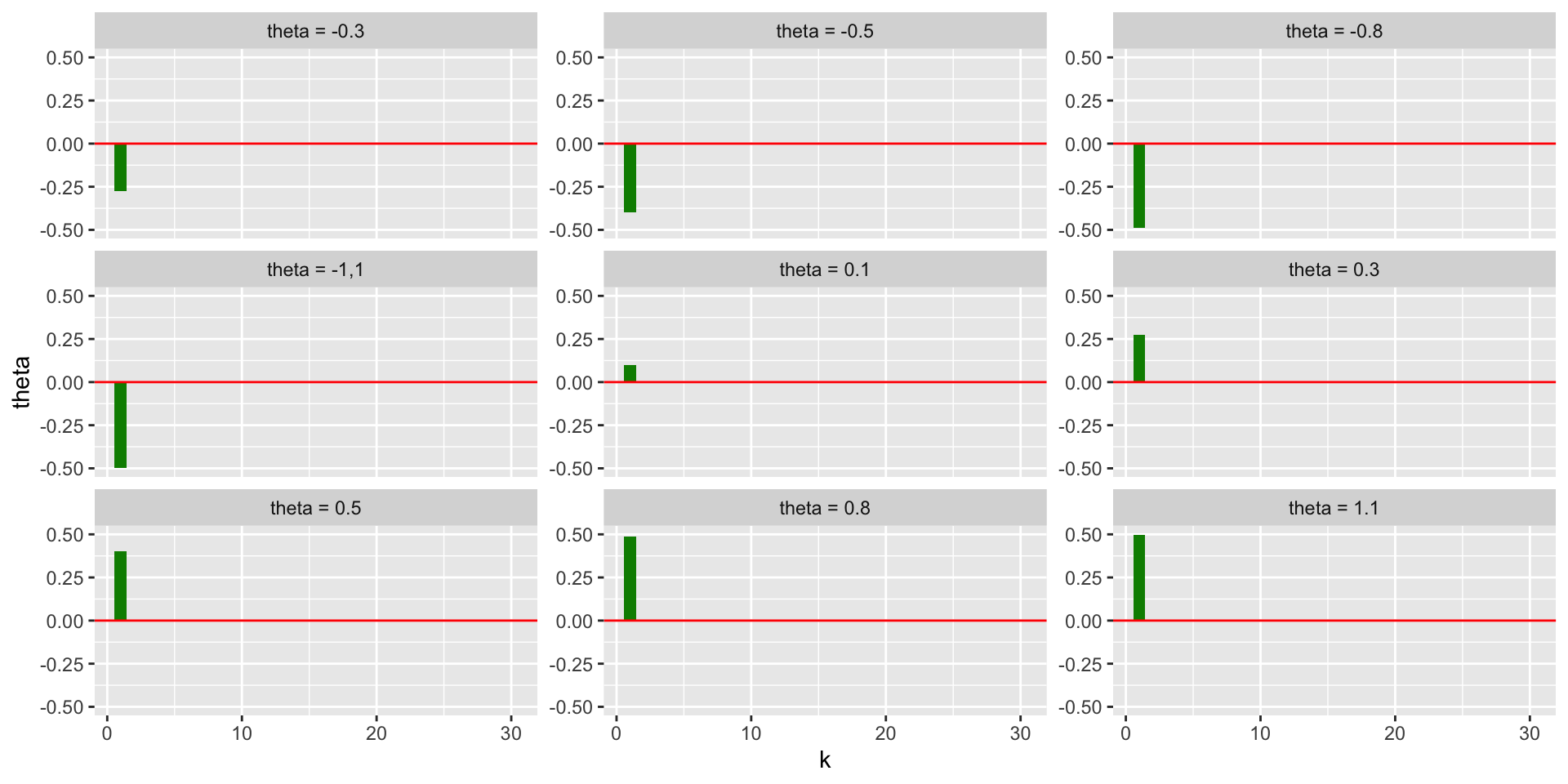
MA(1)

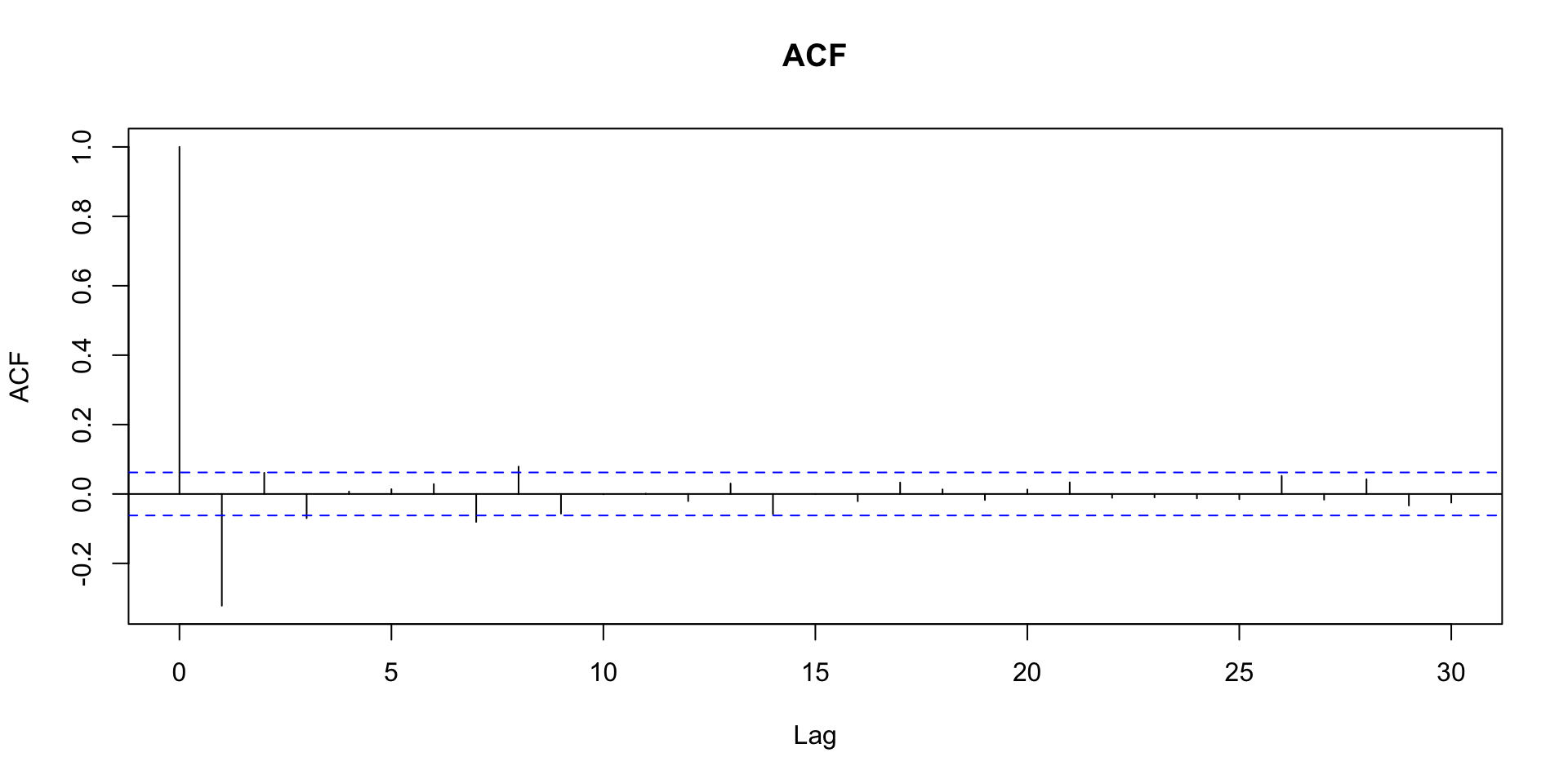
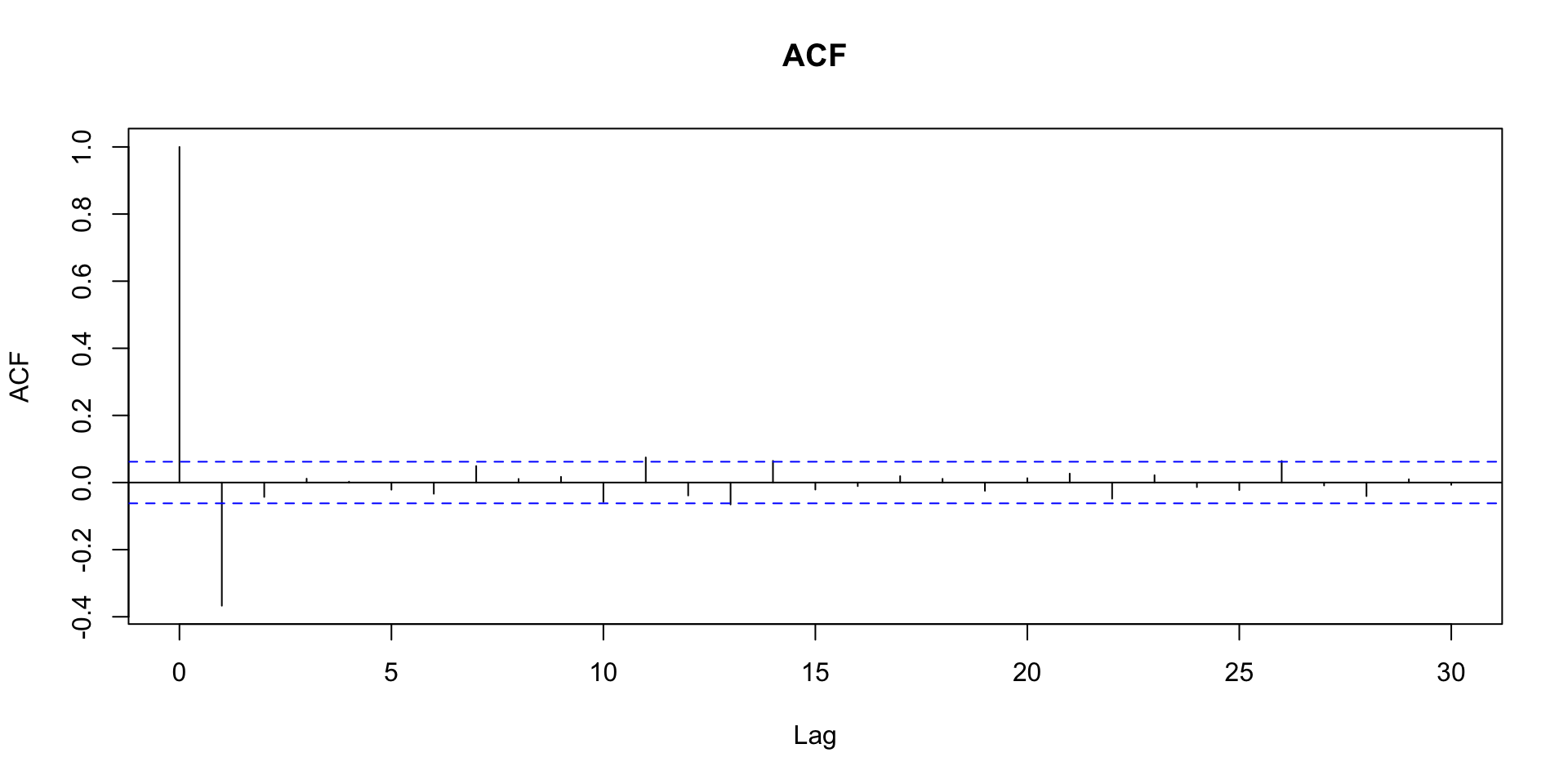
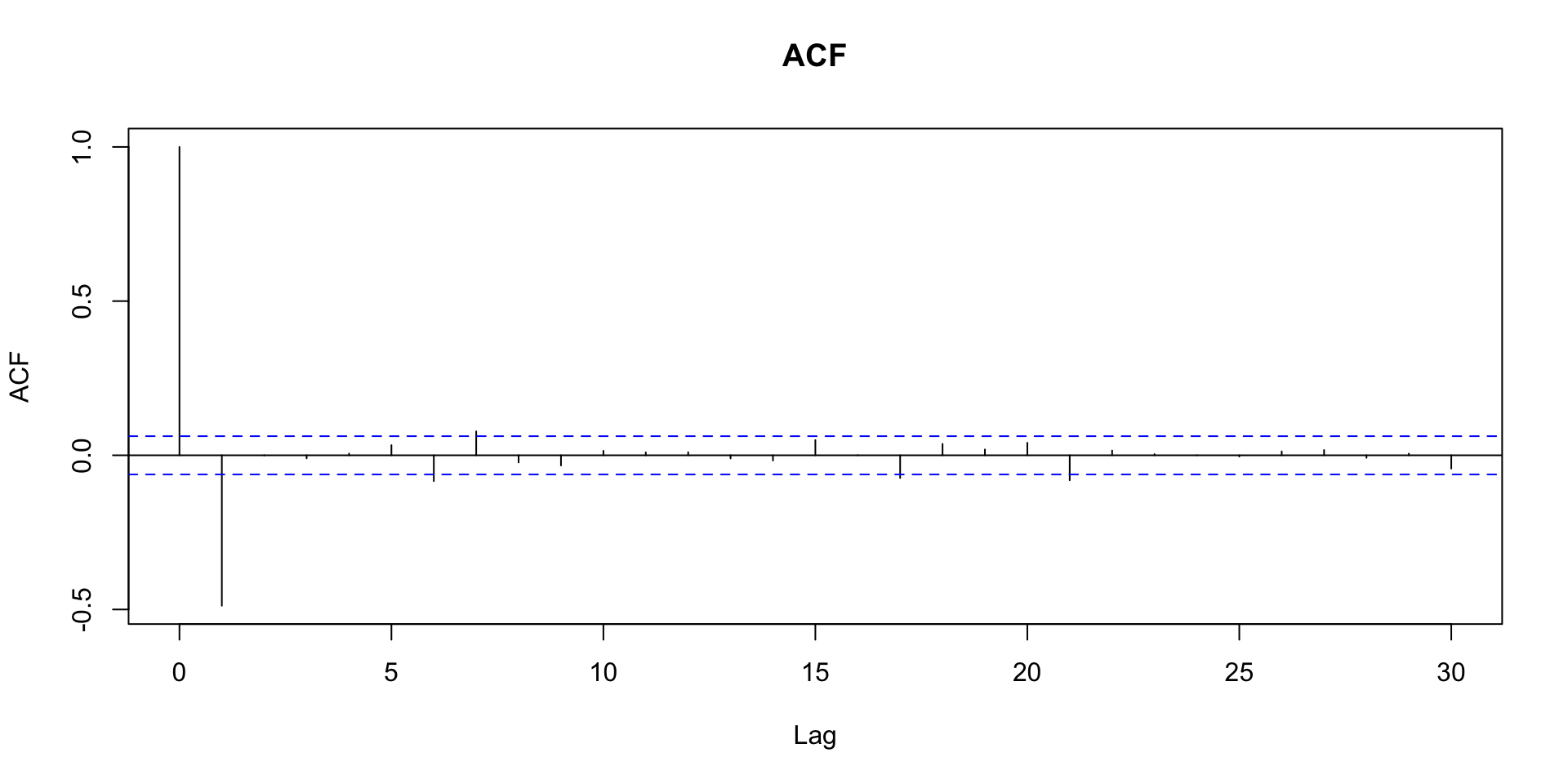
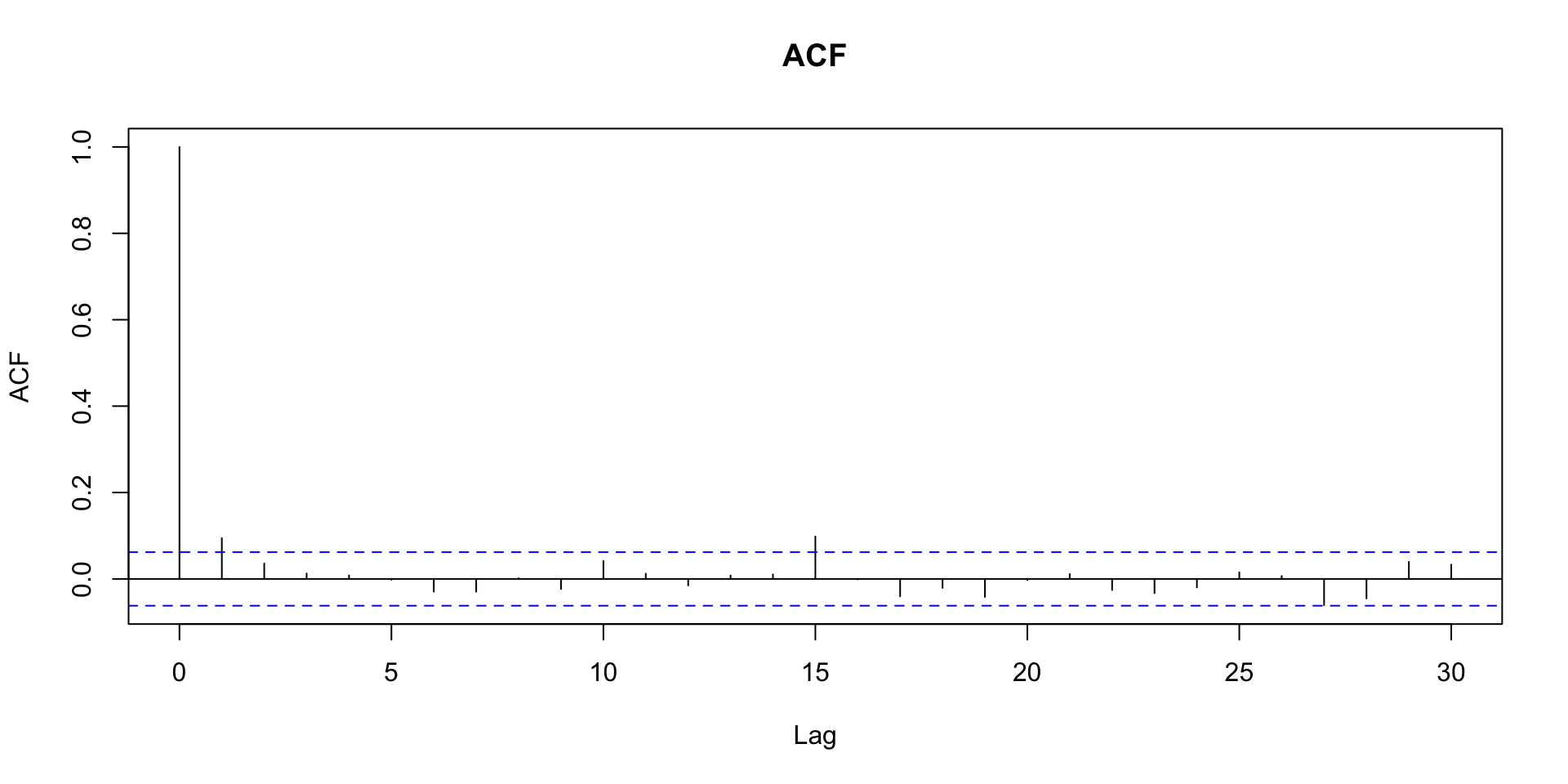
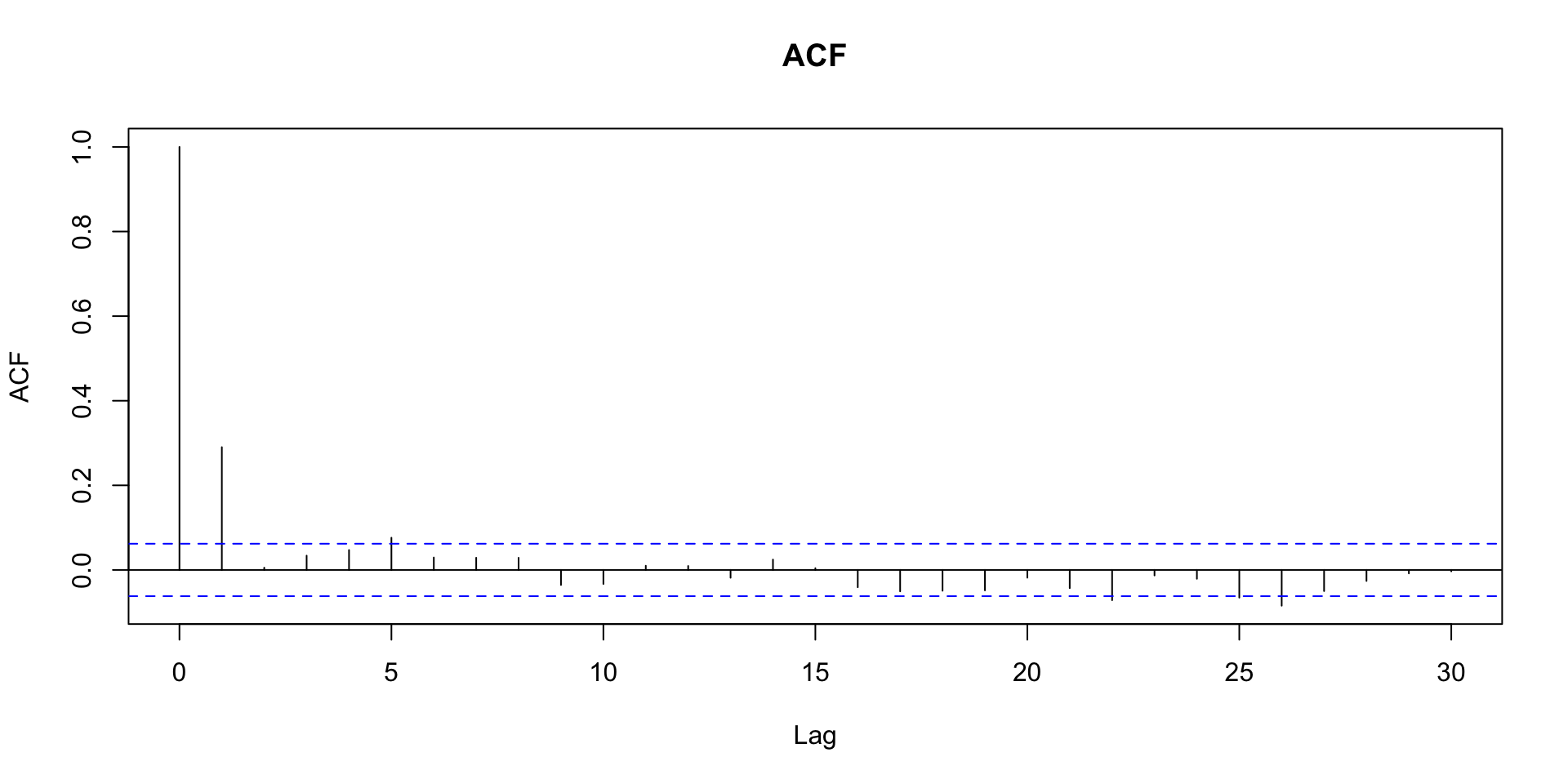
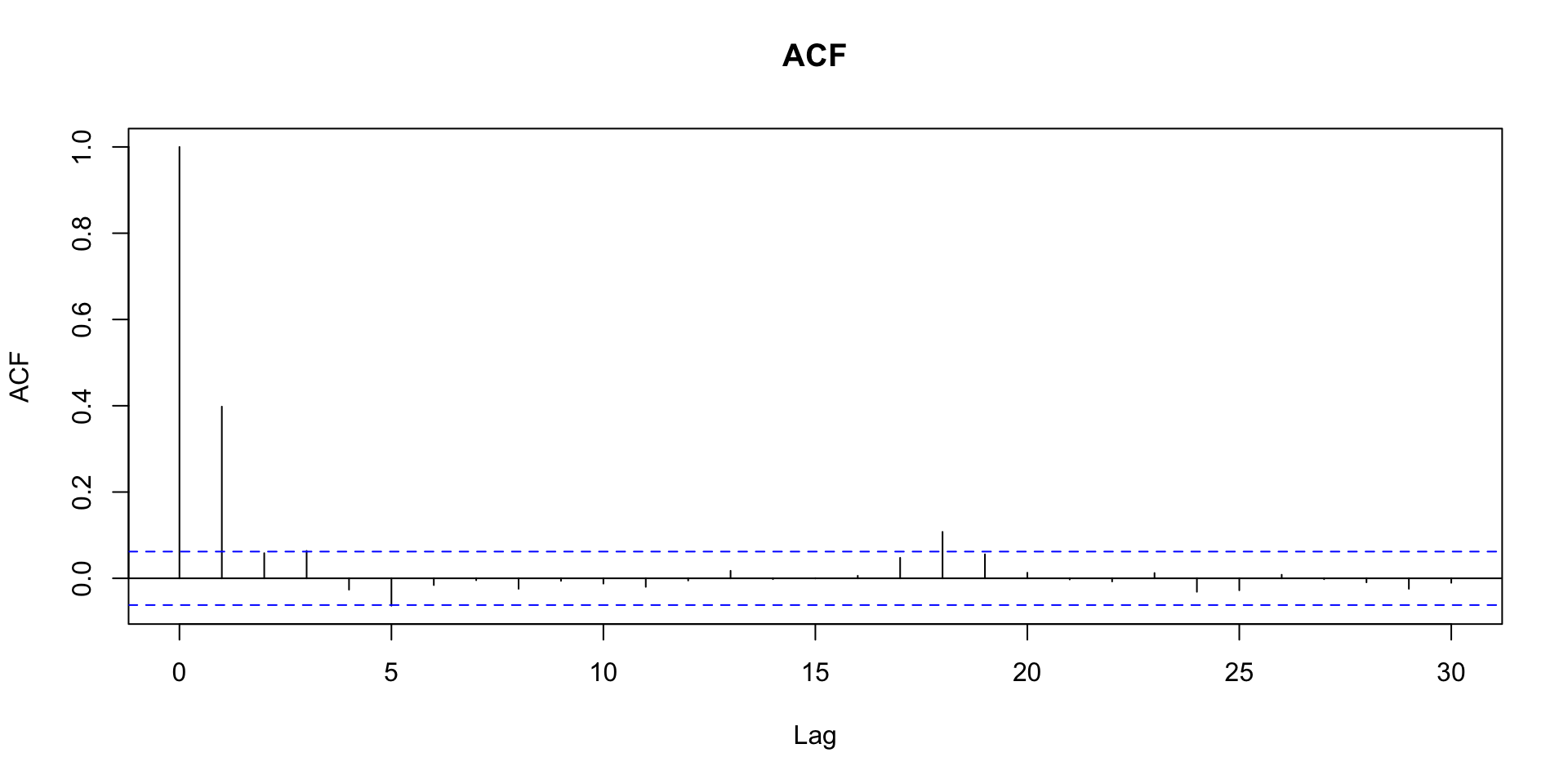
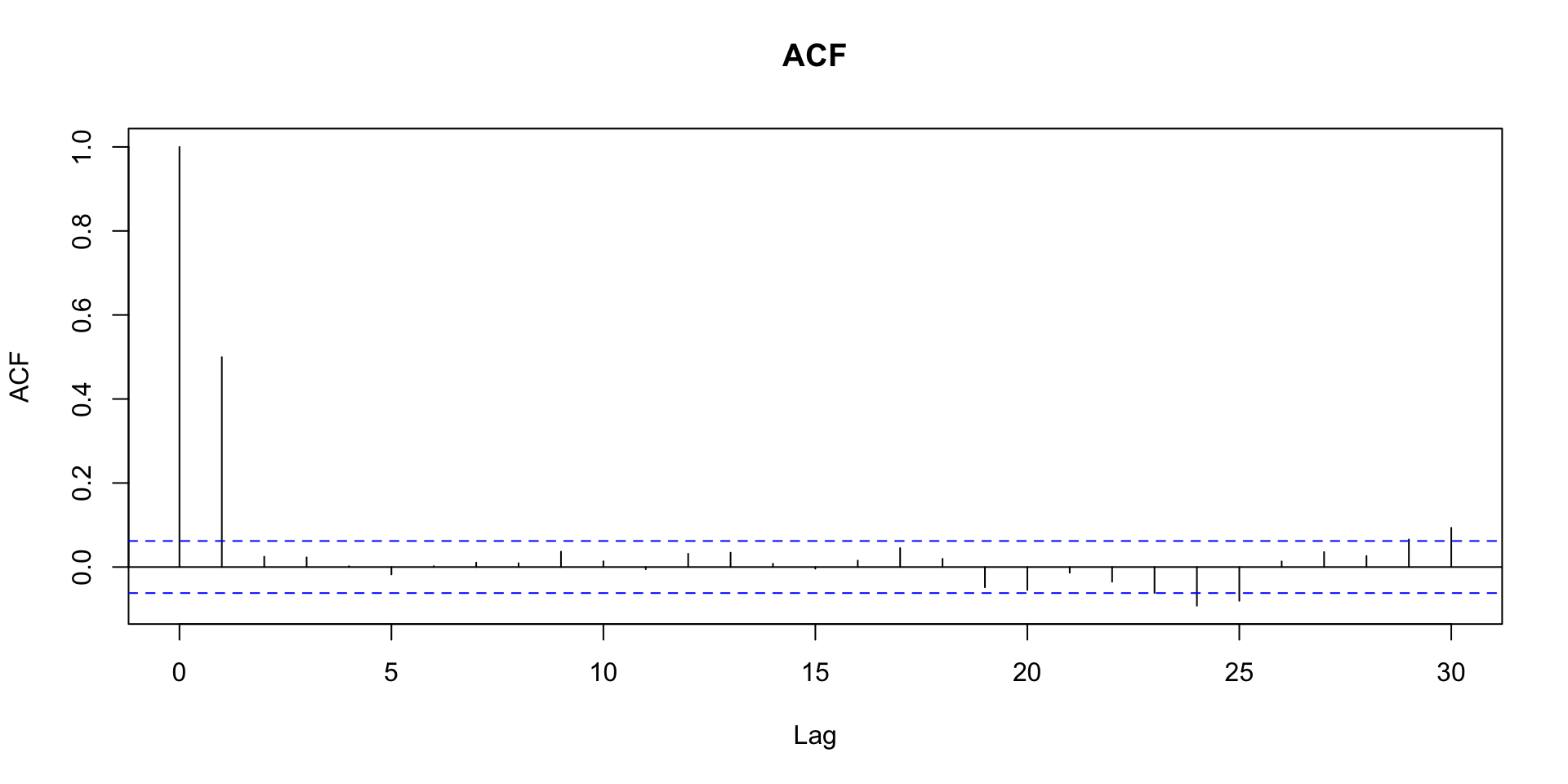
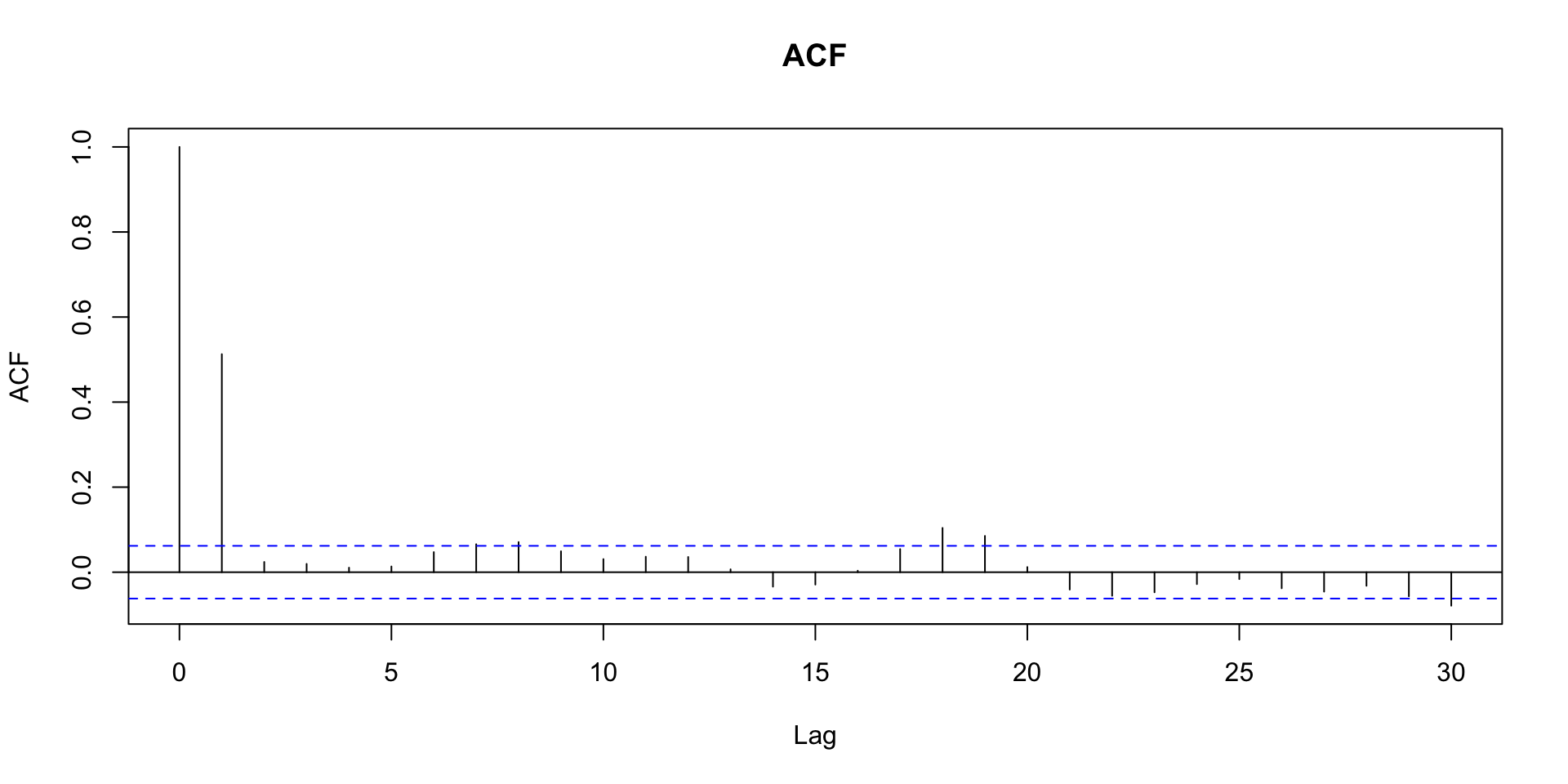
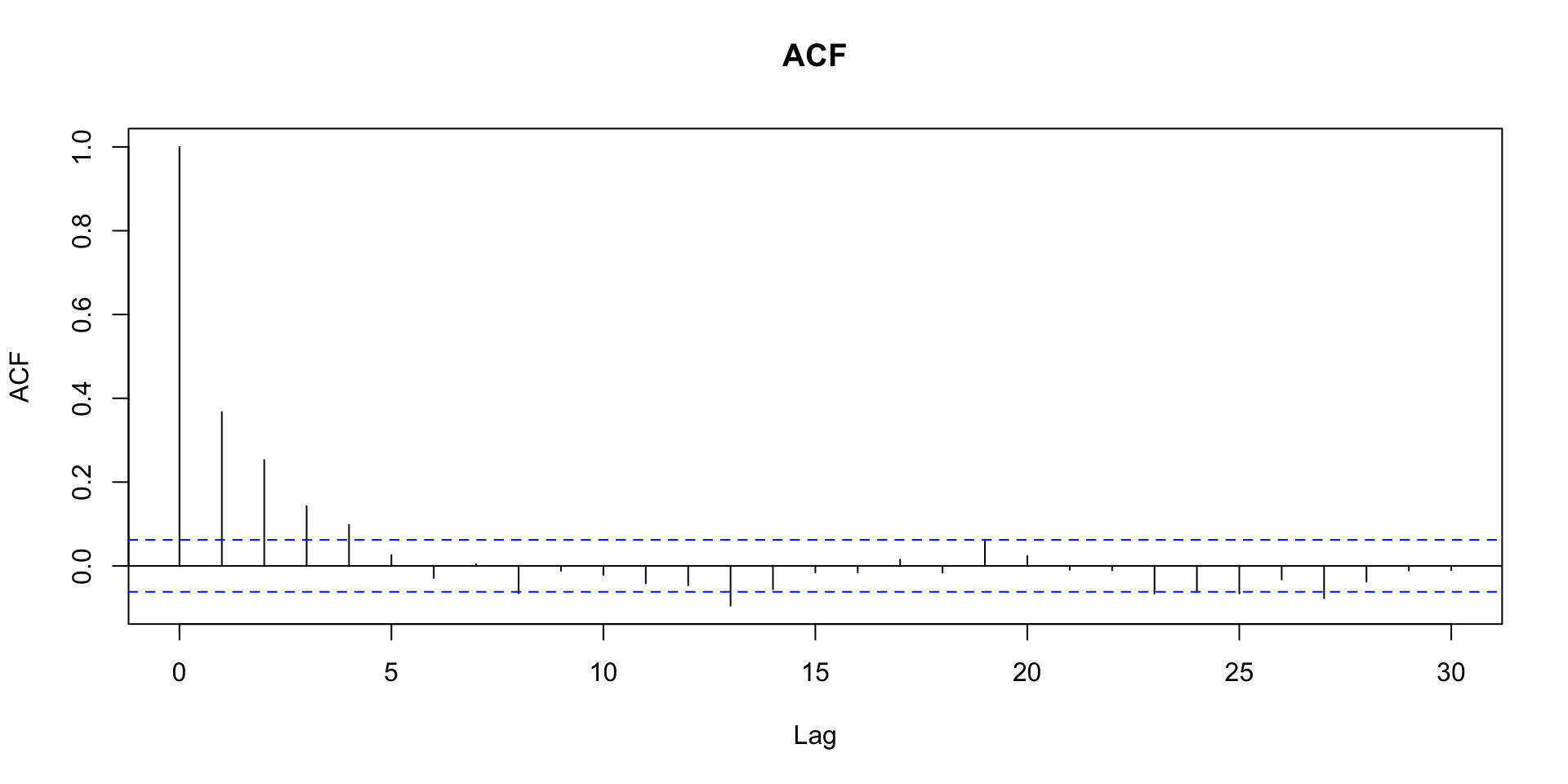
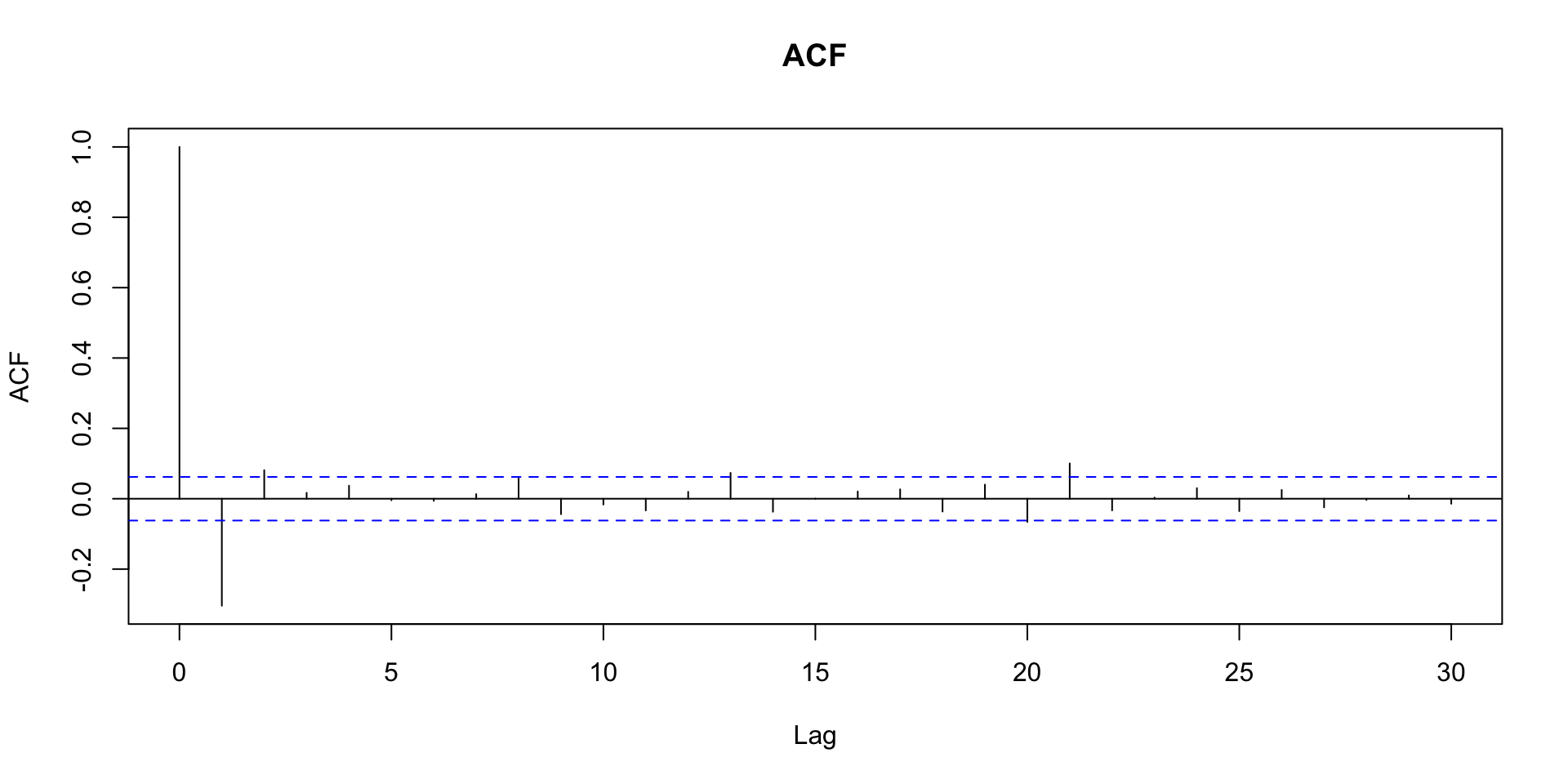
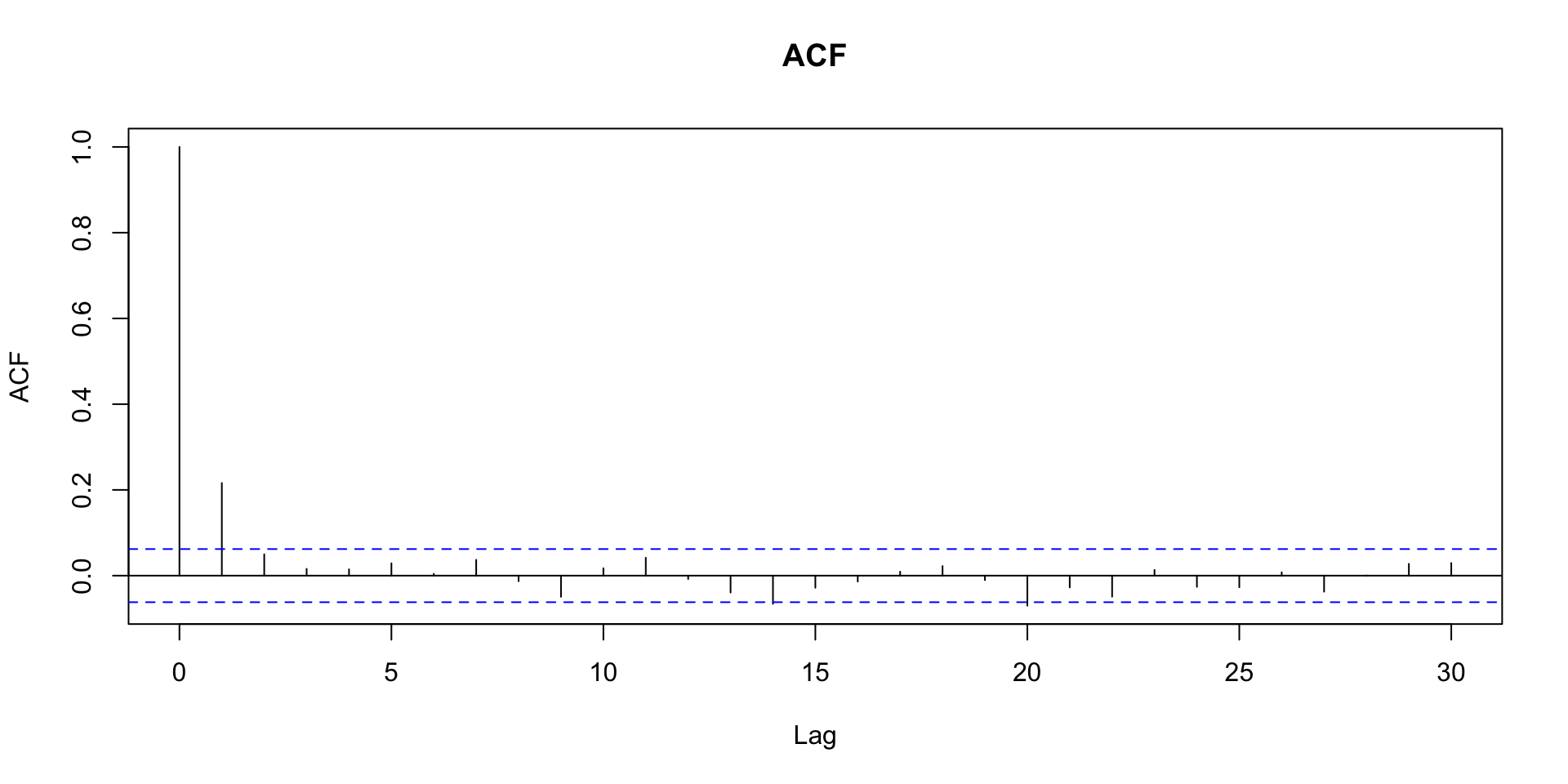
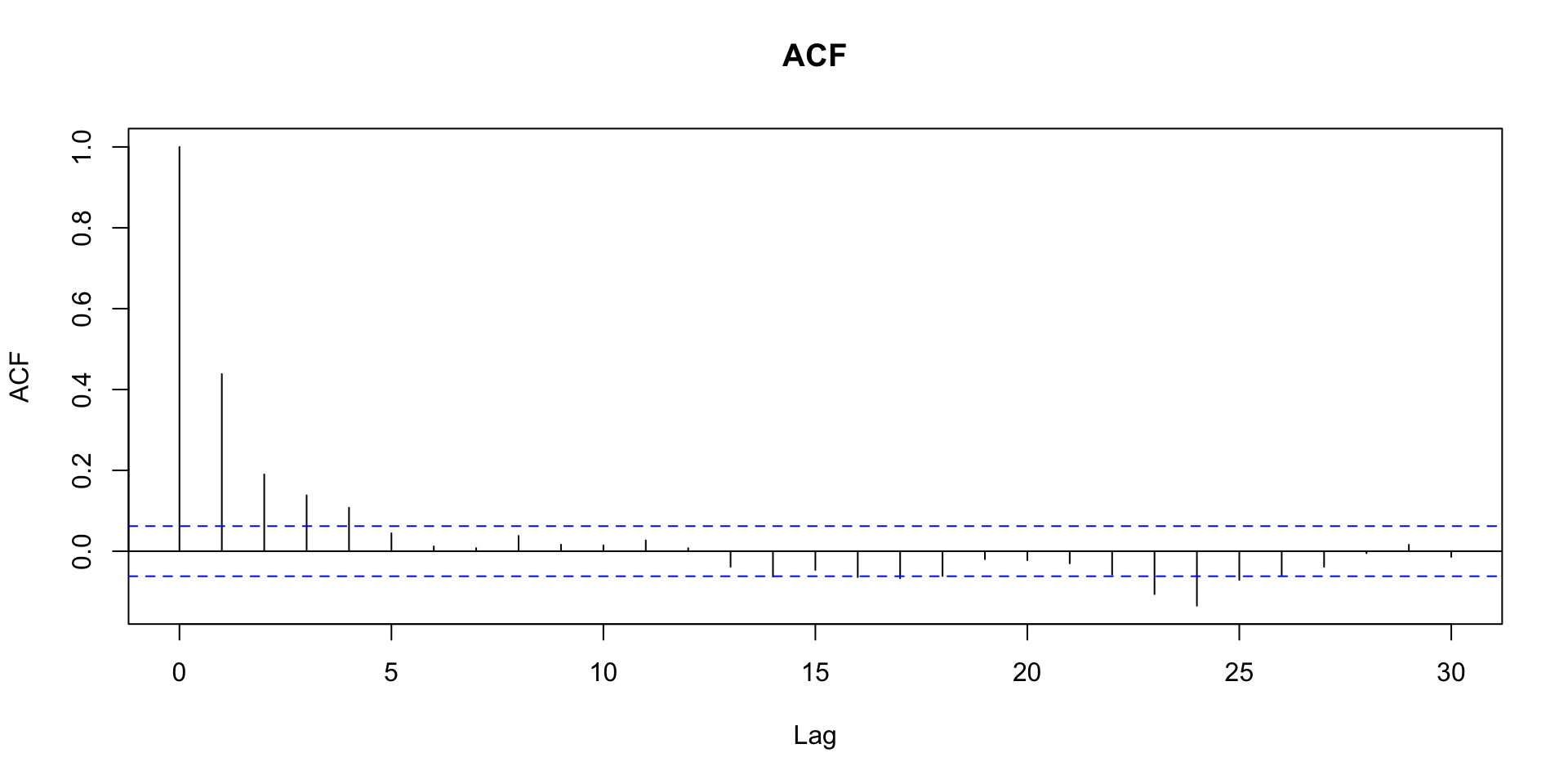
Função de autocorrelação amostral

Code 
y <- arima.sim(model = list(order = c(0, 0, 1), ma = c(-0.3) ), n = 1000)
acf(y, main = "ACF")

Code 
y <- arima.sim(model = list(order = c(0, 0, 1), ma = c(-0.5) ), n = 1000)
acf(y, main = "ACF")

Code 
y <- arima.sim(model = list(order = c(0, 0, 1), ma = c(-0.8) ), n = 1000)
acf(y, main = "ACF")

Code 
y <- arima.sim(model = list(order = c(0, 0, 1), ma = c(-1.1) ), n = 1000)
acf(y, main = "ACF")

Code 
y <- arima.sim(model = list(order = c(0, 0, 1), ma = c(0.1) ), n = 1000)
acf(y, main = "ACF")

Code 
y <- arima.sim(model = list(order = c(0, 0, 1), ma = c(0.3) ), n = 1000)
acf(y, main = "ACF")

Code 
y <- arima.sim(model = list(order = c(0, 0, 1), ma = c(0.5) ), n = 1000)
acf(y, main = "ACF")

Code 
y <- arima.sim(model = list(order = c(0, 0, 1), ma = c(0.8) ), n = 1000)
acf(y, main = "ACF")

MA(2)

MA(2)

Definição:

Um processo estocástico \(\{Y_t\}\) é dito de médias móveis de ordem 2, denotado MA(2), se seu processo gerador de dados é dado por \[Y_t = \mu + \epsilon_t + \theta_1 \epsilon_{t-1} + \theta_2 \epsilon_{t-2},\] em que \(\mu\), \(\theta_1\) e \(\theta_2\) (\(\theta_1, \theta_2 \neq 0\)) são parâmetros reais e \(\epsilon_t \sim RB(0, \sigma^2_{\epsilon})\).

  • \(\mathbb{E}(Y_t) = \mu\)
  • \(\mathbb{V}(Y_t) = (1 + \theta_1^2 + \theta_2^2) \sigma^2_{\epsilon}\)
  • \(\mathbb{C}ov(Y_t, Y_{t-1}) = \sigma^2_{\epsilon} (\theta_1 + \theta_1 \theta_2)\)
  • \(\mathbb{C}ov(Y_t, Y_{t-2}) = \sigma^2_{\epsilon} \theta_2\)
  • \(\mathbb{C}ov(Y_t, Y_{t-k}) = 0, \quad k \geq 2\)

MA(2)

Pode-se verificar que:

  • \(\rho_1 = \dfrac{\theta_1 + \theta_1 \theta_2}{1 + \theta_1^2 + \theta_2^2}\)
  • \(\rho_2 = \dfrac{\theta_2}{1 + \theta_1^2 + \theta_2^2}\)
  • \(\rho_k = 0, \quad k \geq 3.\)

MA(q)

MA(q)

Definição:

Um processo estocástico \(\{Y_t\}\) é dito de médias móveis de ordem q, denotado MA(q), se seu processo gerador de dados é dado por \[Y_t = \mu + \epsilon_t + \theta_1 \epsilon_{t-1} + \theta_2 \epsilon_{t-2} + \cdots + \theta_q \epsilon_{t-q} \equiv Y_t - \mu = (1 + \theta_1B + \cdots + \theta_qB^q)\epsilon_t\] em que \(\mu\), \(\theta_1, \cdots, \theta_q\) (\(\theta_1, \cdots, \theta_q \neq 0\)) são parâmetros reais e \(\epsilon_t \sim RB(0, \sigma^2_{\epsilon})\).

  • \(\mathbb{E}(Y_t) = \mu\)
  • \(\mathbb{V}(Y_t) = (1 + \theta_1^2 + \theta_2^2 + \cdots + \theta_q^2) \sigma^2_{\epsilon}\)
  • \(\mathbb{C}ov(Y_t, Y_{t-k}) = \sigma^2_{\epsilon} (\theta_k + \theta_{k+1}\theta_1 + \theta_{k+2}\theta_2 + \cdots + \theta_q \theta_{q-k}), \quad k = 1, \cdots, q\)
  • \(\rho_k = (\theta_k + \theta_{k+1}\theta_1 + \theta_{k+2}\theta_2 + \cdots + \theta_q \theta_{q-k})/(1 + \theta_1^2 + \theta_2^2 + \cdots + \theta_q^2), \quad k = 1, \cdots, q\)
  • \(\mathbb{C}ov(Y_t, Y_{t-k}) = 0 \quad e \quad \rho_k = 0, \quad k \geq j+1\)

MA(q)

Code 
y <- arima.sim(model = list(order = c(0, 0, 1), ma = .9 ), n = 1000)
acf(y, main = "ACF")

Code 
y <- arima.sim(model = list(order = c(2, 0, 0), ar = c(0.3, 0.15) ), n = 1000)
acf(y, main = "ACF")

Code 
y <- arima.sim(model = list(order = c(0, 0, 2), ma = c(-0.3, 0.15) ), n = 1000)
acf(y, main = "ACF")

Code 
y <- arima.sim(model = list(order = c(0, 0, 2), ma = c(-0.3, -0.15) ), n = 1000)
acf(y, main = "ACF")

Code 
y <- arima.sim(model = list(order = c(1, 0, 0), ar = c(0.14) ), n = 1000)
acf(y, main = "ACF")

Code 
y <- arima.sim(model = list(order = c(0, 0, 4), ma = c(0.4, 0.2, 0.15, 0.1) ), n = 1000)
acf(y, main = "ACF")

Code 
y <- arima.sim(model = list(order = c(0, 0, 1), ma = c(1.2) ), n = 1000)
acf(y, main = "ACF")

MA(q)

  • Nas aulas anteriores estudamos os processos AR(p), processos que se caracterizam por ter muitos coeficientes de autocorrelação diferentes de zero.

  • Estes processos tem memoria longa (pois o valor atual esta correlacionado com todos os anteriores). Isto implica que podemos escrever o processo AR(p) como uma função linear de todas as inovações.

  • Processos AR(p) não conseguem representam séries de memória muito curta (casos em que o valor atual está apenas correlacionado com poucos valores anteriores).

  • Processo MA(q) são úteis para descrever fenômenos nos quais acontecimentos produzem um efeito immediato que duram apenas por curtos períodos de tempo (séries de memória curta).

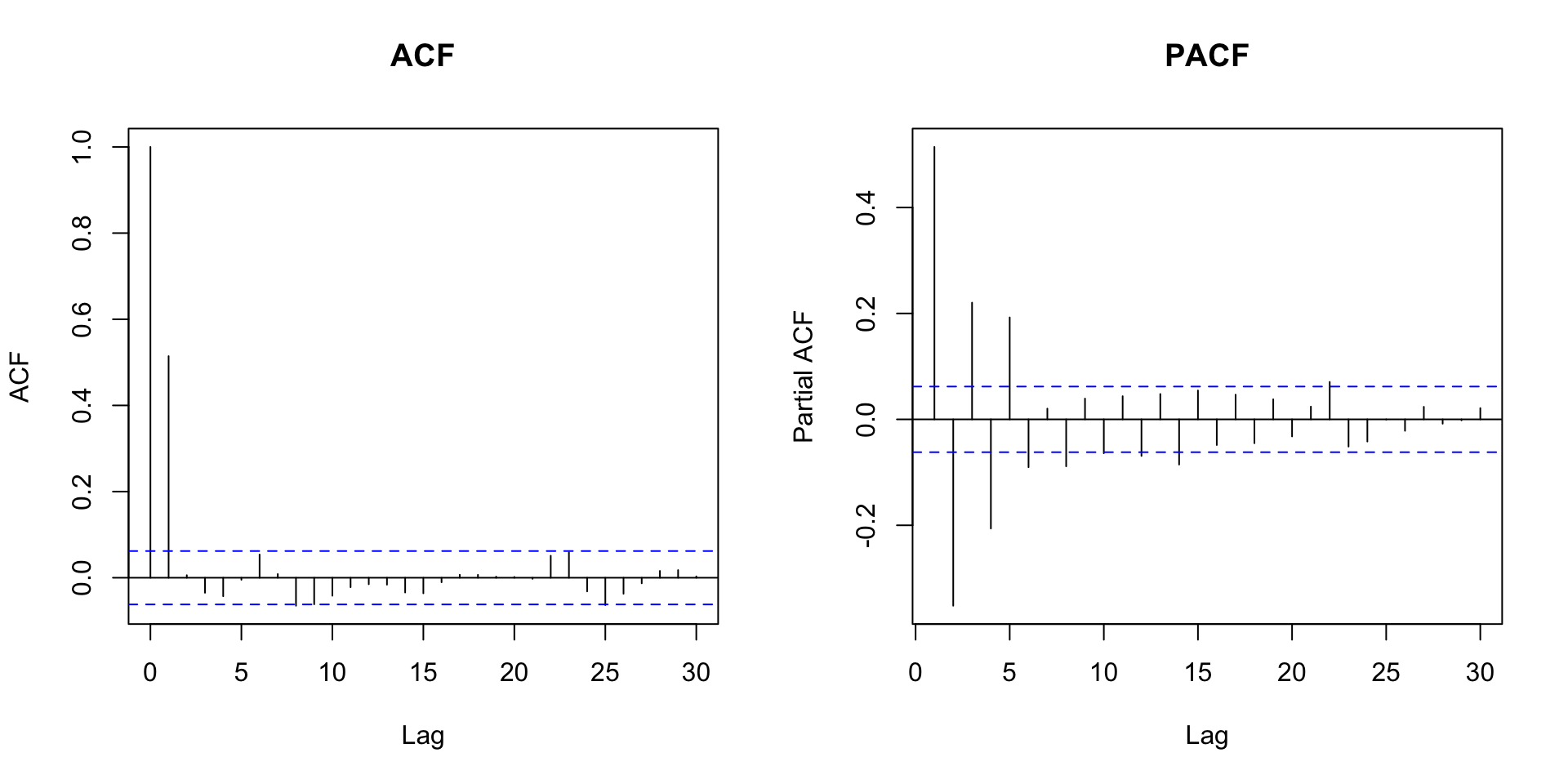
Autocorrelação parcial MA(q)

MA(1)

\[\phi_{kk} = \dfrac{\theta_1^k(1 - \theta_1^2)}{1 - \theta_1^{2(k+1)}}, \quad k \geq 1.\]

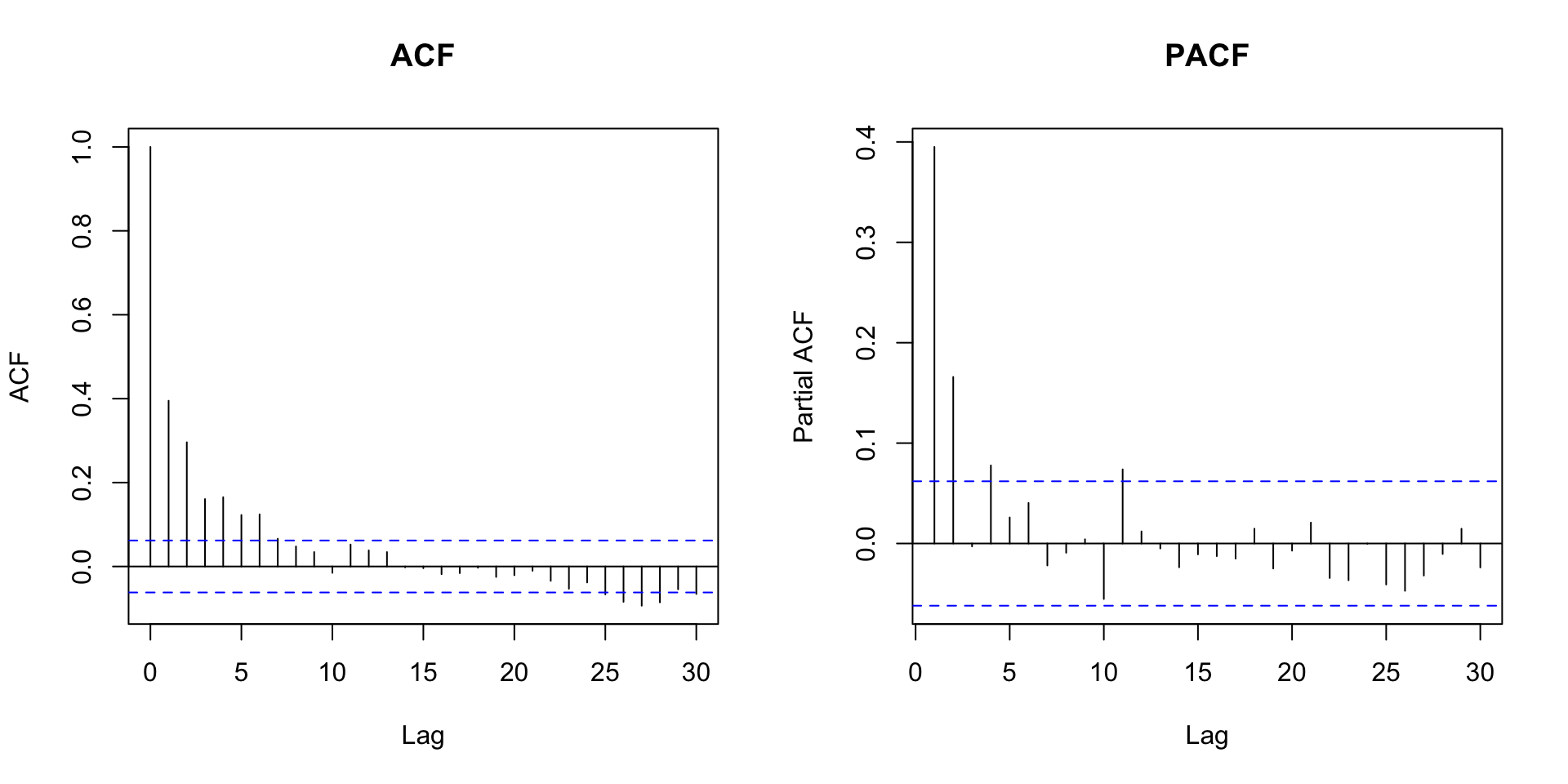
MA(2)

\[\phi_{11} = \rho_1, \quad \phi_{22} = \dfrac{\rho_2 - \rho_1^2}{1-\rho_1^2}, \quad \phi_{33} = \dfrac{\rho_1^3 - \rho_1 \rho_2 (2-\rho_2)}{1-\rho_2^3 - 2 \rho_1^2(1-\rho_2)}, \quad \cdots\]

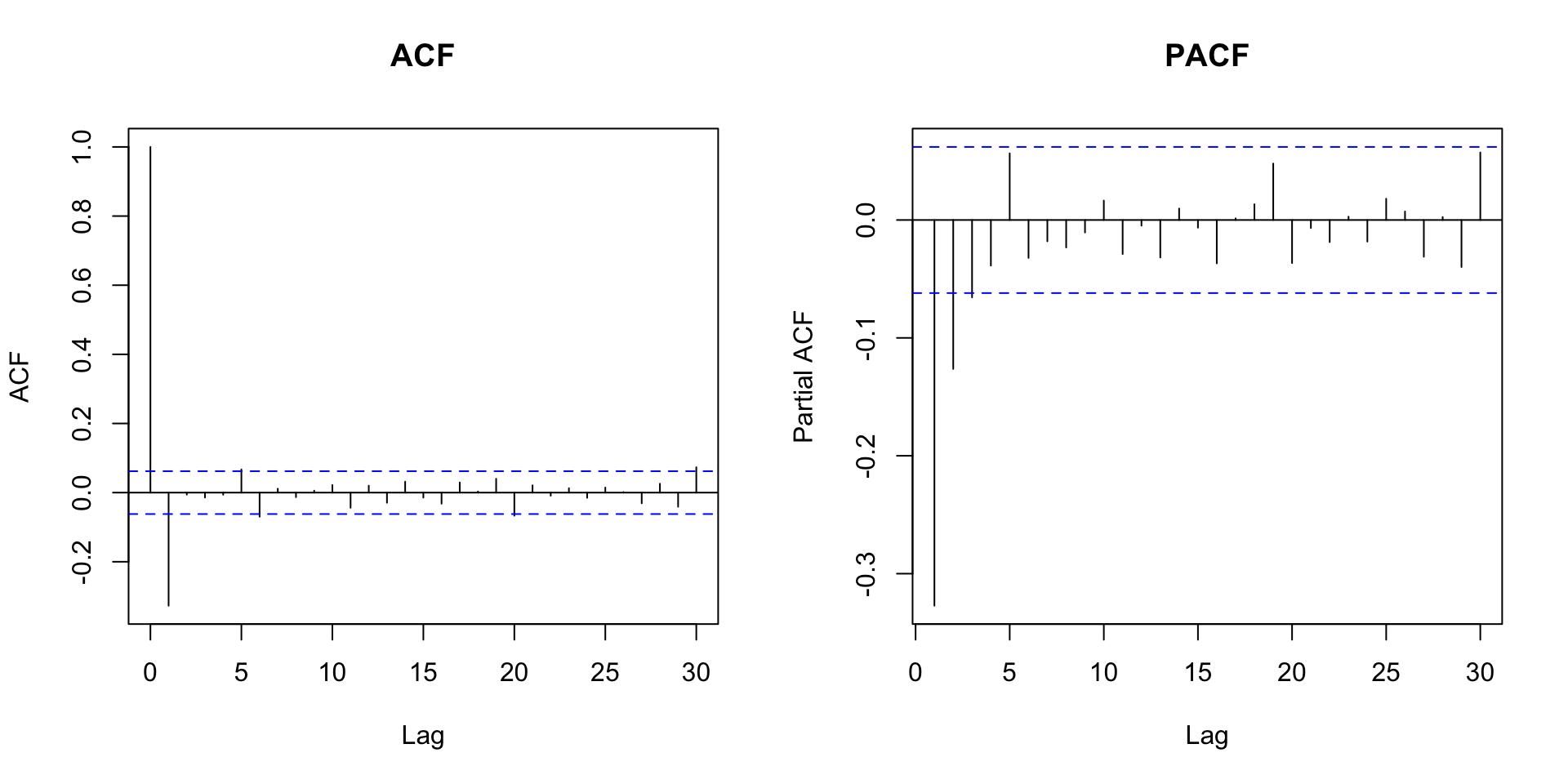
MA(q)

Em geral, a PACF para um MA(q) tem o comportamento de uma mixtura de decaimentos exponenciais ou de ondas senoidais amortecidas.

Autocorrelação parcial MA(q)

Code 
y <- arima.sim(model = list(order = c(0, 0, 1), ma = .9 ), n = 1000)
par(mfrow = c(1, 2))   
acf(y, main = "ACF")
pacf(y, main = "PACF")

Code 
y <- arima.sim(model = list(order = c(2, 0, 0), ar = c(0.3, 0.15) ), n = 1000)
par(mfrow = c(1, 2))   
acf(y, main = "ACF")
pacf(y, main = "PACF")

Code 
y <- arima.sim(model = list(order = c(0, 0, 1), ma = -0.4), n = 1000)
par(mfrow = c(1, 2))   
acf(y, main = "ACF")
pacf(y, main = "PACF")

Code 
y <- arima.sim(model = list(order = c(0, 0, 2), ma = c(-0.3, -0.15) ), n = 1000)
par(mfrow = c(1, 2))   
acf(y, main = "ACF")
pacf(y, main = "PACF")

Code 
y <- arima.sim(model = list(order = c(1, 0, 0), ar = c(0.14) ), n = 1000)
par(mfrow = c(1, 2))   
acf(y, main = "ACF")
pacf(y, main = "PACF")

Code 
y <- arima.sim(model = list(order = c(0, 0, 2), ma = c(0.4, 0.2) ), n = 1000)
par(mfrow = c(1, 2))   
acf(y, main = "ACF")
pacf(y, main = "PACF")

Code 
y <- arima.sim(model = list(order = c(0, 0, 1), ma = c(1.2) ), n = 1000)
par(mfrow = c(1, 2))   
acf(y, main = "ACF")
pacf(y, main = "PACF")

\(MA(\infty)\)

\(MA(\infty)\)

Definição:

Quando \(q = \infty\), o processo MA(q) pode ser escrito como \[Y_t = \mu + \displaystyle \sum_{i=0}^{\infty} \psi_j \epsilon_t = \mu + \psi(L) \epsilon_t,\] em que \(\psi_0 = 1\) e \(\psi(L) = (1 + \psi_1B + \psi_2B^2 + \cdots)\).

Se o processo for estacionário, então \(\displaystyle \sum_{i=0}^{\infty} \psi_j^2 < \infty\).

Invertibilidade

Invertibilidade

  • Quando estudamos os modelos AR(p), vimos que causalidade implica em escrever um AR(p) como um MA(\(\infty\)) (o que acontece se o processo AR(p) for estacionário).
  • Invertibilidade significa escrever um MA(q) como um AR(\(\infty\)), o que acontece apenas se certas condições são satisfetitas.

Seja o processo MA(1), \[Y_t - \mu = \underbrace{\epsilon_t + \theta \epsilon_{t-1}}_{(1 + \theta B)\epsilon_t}\]

Se \(|\theta| < 1\), \[(Y_t - \mu)(1 + \theta B)^{-1} = \epsilon_t \rightarrow (Y_t - \mu)(1 - \theta B +\theta^2 B^2 - \theta^3 B^3 + \cdots) = \epsilon_t\]

\(\rightarrow \tilde{Y}_t = \theta \tilde{Y}_{t-1} - \theta^2 \tilde{Y}_{t-2} + \theta^3 \tilde{Y}_{t-3} + \cdots + \epsilon_t\)

Relação entre AR(p) e MA(q)

Relação entre AR(p) e MA(q)

Para um AR(p) estacionário, \[\begin{align*} \tilde{Y}_t = \phi_1 \tilde{Y}_{t-1} + \cdots + \phi_p \tilde{Y}_{t-p} &+ \epsilon_t \\ \tilde{Y}_t - \phi_1 \tilde{Y}_{t-1} - \cdots - \phi_p \tilde{Y}_{t-p} &= \epsilon_t \\ (1 - \phi_1 B - \cdots - \phi_p B^p) \tilde{Y}_t &= \epsilon_t \\ \phi_p(B) \tilde{Y}_t &= \epsilon_t \\ \tilde{Y}_t = \dfrac{1}{\phi_p(B)} & \epsilon_t, \\ \tilde{Y}_t = \psi(B) & \epsilon_t, \\ \end{align*},\] em que \(\psi(B) = 1 + \psi_1B + \psi_2 B^2 + \cdots\), tal que \(\phi_p(B)\psi(B) = 1\)

Relação entre AR(p) e MA(q)

Para um AR(1), \[\begin{align*} \tilde{Y}_{t}(1 - \phi B) &= \epsilon_t \\ \tilde{Y}_{t} &= (1 + \psi_1 B + \psi_2 B^2 + \cdots)\epsilon_t \\ \end{align*}\]

O que implica que \((1-\phi B)(1 + \psi_1 B + \psi_2 B^2 + \cdots) = 1\)

Para obtermos os \(\psi\)s, basta garantir que \((1-\phi B)(1 + \psi_1 B + \psi_2 B^2 + \cdots) = 1\) seja satisfeito.

\[1 + \psi_1 B + \psi_2 B^2 + \cdots - \phi B - \phi \psi_1 B^2 + \phi \psi_2 B^3 = 1\]

  • \((\psi_1 - \phi) = 0 \rightarrow \psi_1 = \phi\).
  • \((\psi_2 - \phi \psi_1) = 0 \rightarrow \psi_2 = \phi^2\)
  • \(\cdots \rightarrow \psi_k = \phi^k, \quad k \geq 2\)

Relação entre AR(p) e MA(q)

Para um AR(2), \[\begin{align*} \tilde{Y}_{t}(1 - \phi_1 B - \phi_2 B^2) &= \epsilon_t \\ \tilde{Y}_{t} &= (1 + \psi_1 B + \psi_2 B^2 + \cdots)\epsilon_t \\ \end{align*}\]

O que implica que \((1-\phi_1 B - \phi_2 B^2)(1 + \psi_1 B + \psi_2 B^2 + \cdots) = 1\)

Para obtermos os \(\psi\)s, basta garantir que \((1-\phi_1 B - \phi_2 B^2)(1 + \psi_1 B + \psi_2 B^2 + \cdots) = 1\) seja satisfeito.

\[1 + \psi_1 B + \psi_2 B^2 + \cdots - \phi_1 B - \phi_1 \psi_1 B^2 - \phi_1 \psi_2 B^3 - \cdots - \phi_2 B^2- \phi_2 \psi_1 B^3 - \cdots = 1\]

  • \((\psi_1 - \phi_1) = 0 \rightarrow \psi_1 = \phi_1\)
  • \((\psi_2 - \psi_1 \phi_1 - \phi_2) = 0 \rightarrow \psi_2 = \psi_1 \phi_1 + \phi_2\)
  • \((\psi_3 - \psi_2 \phi_1 - \psi_1 \phi_2) = 0 \rightarrow \psi_3 = \psi_2 \phi_1 + \psi_1 \phi_2\)
  • \(\cdots \rightarrow \psi_k = \psi_{k-1}\phi_1 + \psi_{k-2}\phi_2, \quad k \geq 2\)

Relação entre AR(p) e MA(q)

Para um processo MA(q) invertível, \[\begin{align*} \tilde{Y}_t &= \underbrace{\epsilon_t + \theta_1 \epsilon_{t-1} + \cdots + \theta_q \epsilon_{t-q}}_{(1 + \theta_1 B + \theta_2 B^2 + \cdots + \theta_q B^q) \epsilon_t} \\ \tilde{Y}_t &= \theta_q(B) \epsilon_t \\ \pi(B) \tilde{Y}_t &= \epsilon_t \\ \end{align*},\] em que \(\pi(B) = 1 + \pi_1B + \pi_2 B^2 + \cdots\), tal que \(\theta_q(B)\pi(B) = 1\)

Para obter os valores dos \(\pi\)s, basta proceder em forma semelhante ao feito para ao processo AR(p).

Relação entre AR(p) e MA(q)

Para um MA(2), \[\begin{align*} \tilde{Y}_{t} = (1 + \theta_1 B + \theta_2 B^2) &\epsilon_t \\ \tilde{Y}_{t} (1 + \pi_1 B + \pi_2 B^2 + \cdots ) = & \epsilon_t \\ \end{align*}\]

O que implica que \((1 + \theta_1 B + \theta_2 B^2)(1 + \pi_1 B + \pi_2 B^2 + \cdots) = 1\)

Para obtermos os \(\pi\)s, basta garantir que \((1 + \theta_1 B + \theta_2 B^2)(1 + \pi_1 B + \pi_2 B^2 + \cdots) = 1\) seja satisfeito.

\[1 + \pi_1 B + \pi_2 B^2 + \cdots + \theta_1 B + \theta_1 \pi_1 B^2 + \theta_1 \pi_2 B^3 + \cdots \theta_2 B^2 + \theta_2 \pi_1 B^3 + \theta_2 \pi_2 B^4 + \cdots = 1\]

  • \((\pi_1 + \theta_1 ) = 0 \rightarrow \pi_1 = - \theta_1\)
  • \((\pi_2 + \theta_1 \pi_1 + \theta_2) = 0 \rightarrow \pi_2 = - \pi_1 \theta_1 - \theta_2\)
  • \(\cdots \rightarrow \pi_k = - \pi_{k-1}\theta_1 - \pi_{k-2}\theta_2, \quad k \geq 3\)

Relação entre AR(p) e MA(q)

Todo processo estacionário AR(p) (p < \(\infty\)) pode ser escrito como um MA(\(\infty\)) e todo processo MA(q) invertível (q < \(\infty\)) pode ser escrito como um AR(\(\infty\)).

Referências

Carlos Trucíos (IMECC/UNICAMP) | ME607 - Séries Temporais | ctruciosm.github.io