Instituto de Matemática, Estatística e Computação Científica (IMECC), Universidade Estadual de Campinas (UNICAMP).
Introdução
Introdução
Já aprendimos a identificar processos AR(p) através da ACF e PACF.
Aprendimos também como estimar os parâmetros do modelo.
Agora aprenderemos a fazer diagnóstico do modelo e previsão.
Diagnóstico
Diagnóstico
Como sabermos se o modelo ajustado capturou a dinâmica dos dados?
Diagnóstico do modelo!
Na formulação do modelo, assumiu-se que os erros são ruido branco. Se o modelo for adequado, os resíduos deverão estar próximos de erros e, por tanto, deverão ser aproximadamente um ruido branco.
Diagnóstico
Como verificar se os resíduos são ruido branco?
ACF
PACF
Testes de Ljung-Box
Homocedasticidade
Normalidade*
Rejeitarmos a hipótese de que erros são ruido branco implica que ainda há informação não capturada pelo modelo (o que pode gerar previsões ruins) que pode ser melhor explorada por outros modelos (e pode gerar melhores previsões). Neste caso, descarta-se o modelo ajustado e testam-se outras possibilidades até obtermos um modelo em que não podemos rejeitar a hipótese de que os erros são ruido branco.
Diagnóstico
Seja o processo AR(p) \[Y_t = c + \phi_1Y_{t-1} + \cdots + \phi_p Y_{t-p} + \epsilon_t.\]
Definimos os resíduos como \[\hat{\epsilon}_t = y_t - \hat{c}- \hat{\phi}_1 y_{t-1} - \cdots - \hat{\phi}_p y_{t-p}\]
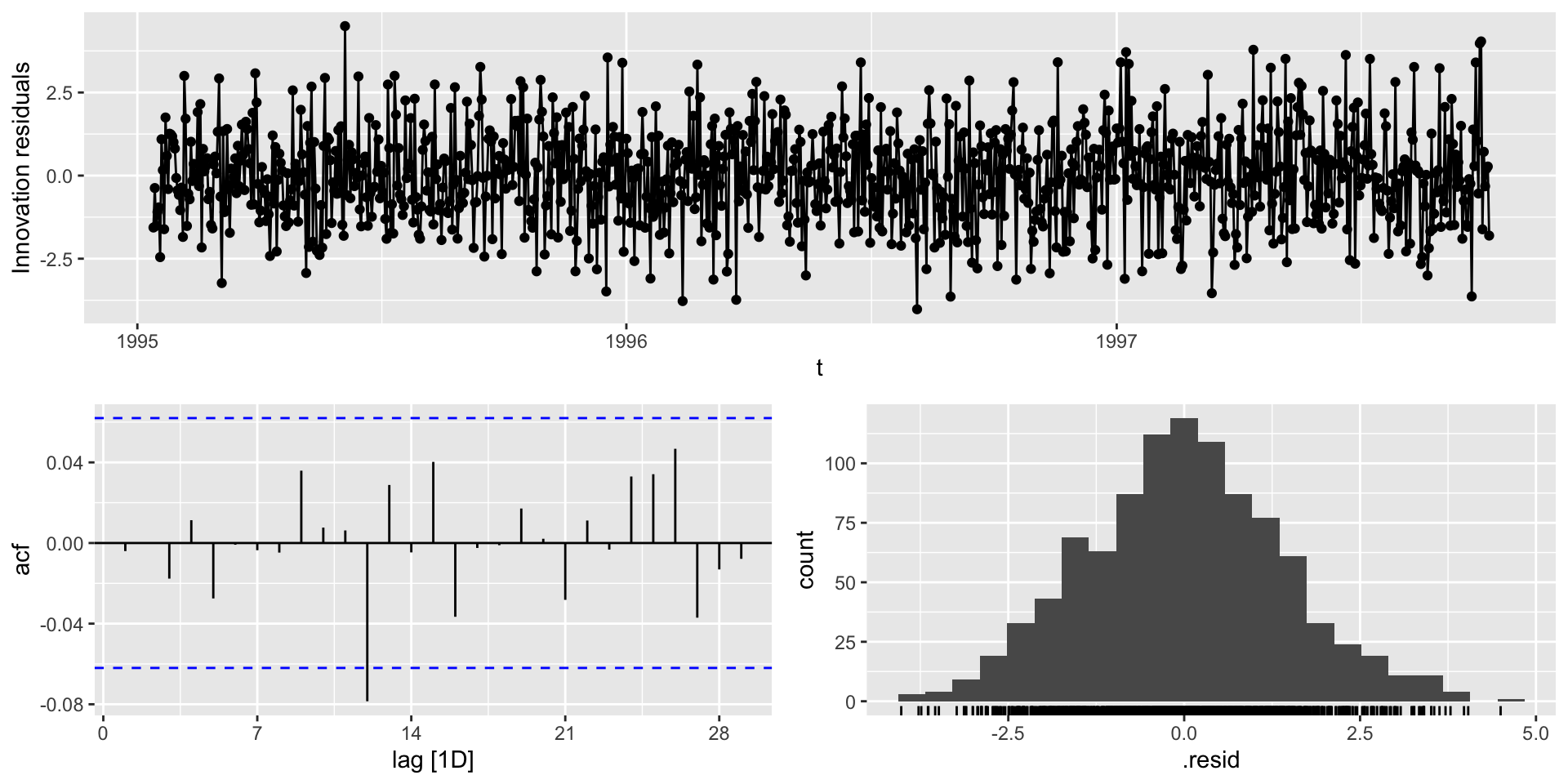
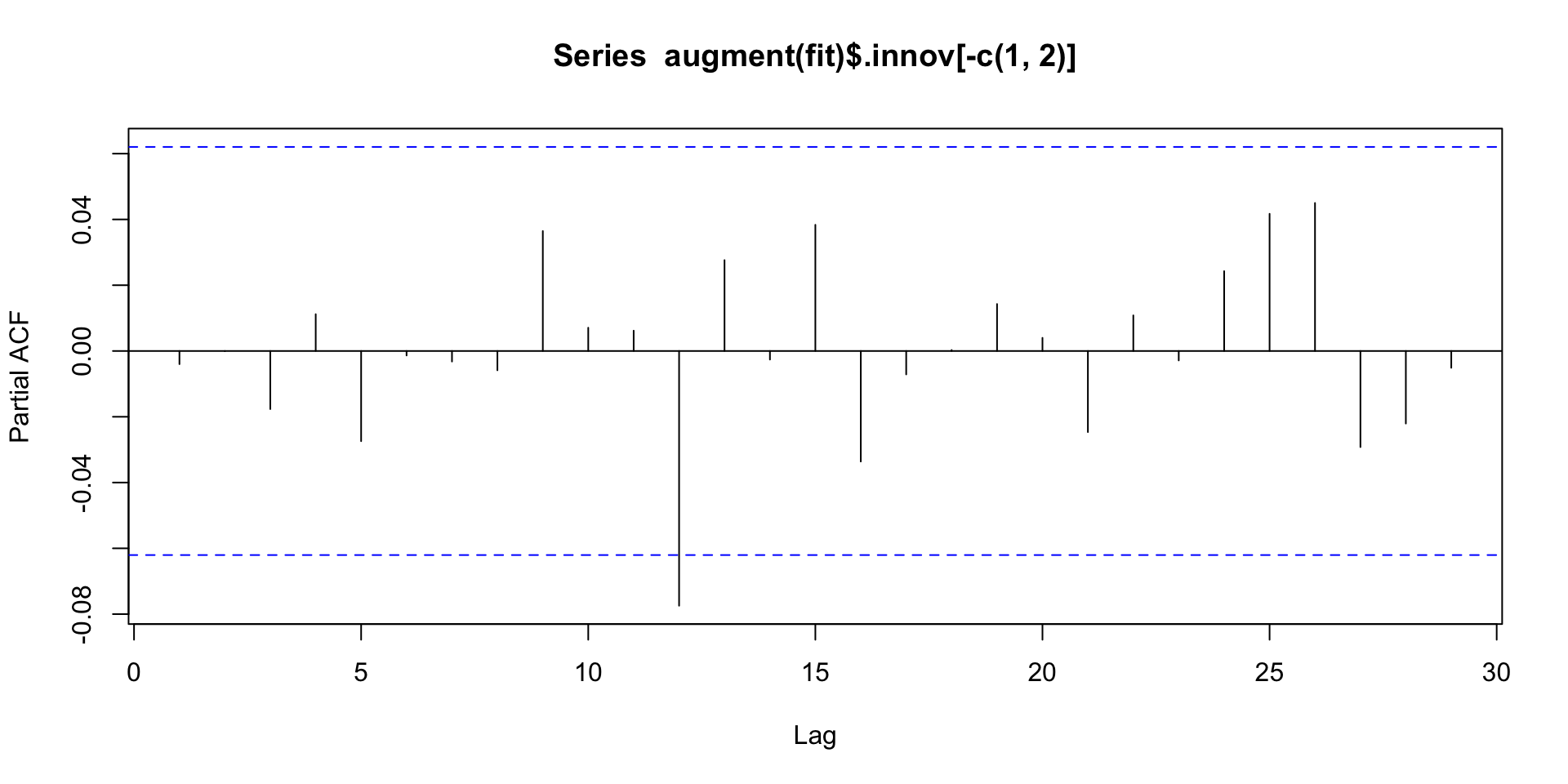
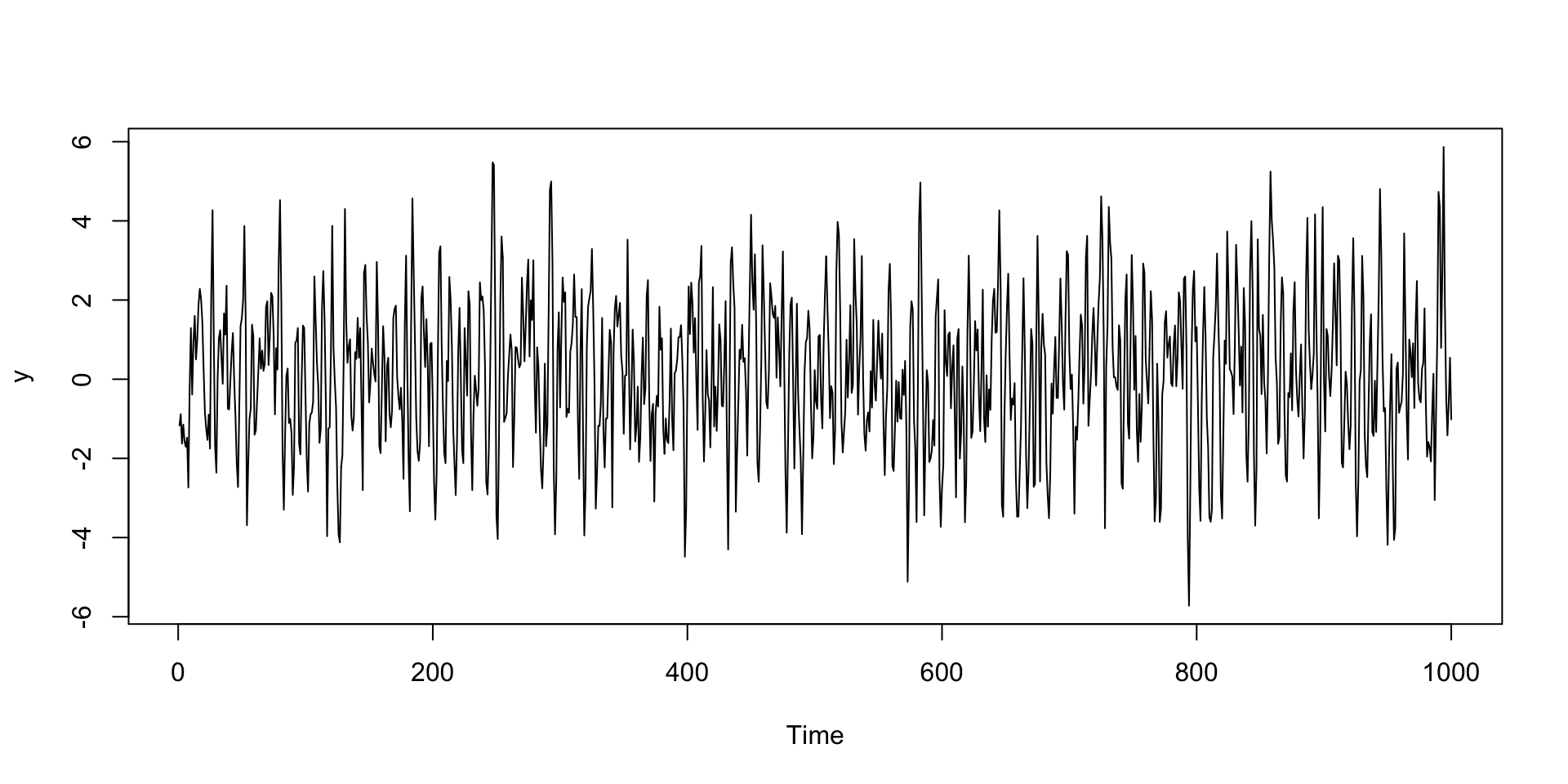
A primeira forma de verificar se os erros (\(\{ \epsilon_t \}\)) são ruido branco é através do gráfico de sequência, ACF e PACF dos resíduos (\(\{ \hat{\epsilon_t} \}\)).
Se \(\{ \hat{\epsilon_t} \}_{t \geq 1}\) for ruido branco: (a) nenhum padrão deveria ser observado no gráfico de sequência, (b) ACF não deveriam indicar \(\rho_k \neq 0\) e (c) PACF não deveriam indicar \(\phi_{kk} \neq 0\).
Em particular, deveriamos ter que, aproximadamente \[\hat{\rho}_k \sim N(0, 1/n).\]
Contudo, \(\mathbb{V}(\hat{\rho}_k)\) pode ser bem menor do que \(1/n\). Por exemplo, Box, Jenkins e Reinsel (1994) provam que, para um AR(1), \[\mathbb{V}(\hat{\rho}_k) \approx \dfrac{1}{n}[1 - \phi^{2(k-1)}(1-\phi^2)].\]
Para \(k\) grande, \(\approx \dfrac{1}{n}\) mas para \(k\) pequeno, a variância pode ser bem menor.
De qualquer modo, a comparação com \(\pm 2/\sqrt{n}\) fornece uma indicação geral da possível quebra de comportamento ruído branco.
Diagnóstico
Teste LM
Também conhecido como teste Breusch-Godfrey, é utilizado para testar autocorrelação dos resíduos. Consiste em regredir os resíduos com seus valores defasados: \[\hat{\epsilon}_t = \beta_1 \hat{\epsilon}_{t-1} + \cdots + \beta_h \hat{\epsilon}_{t-h} + u_t.\]
\[H_0: \beta_1 = \beta_2 = \cdots = \beta_h = 0 \quad vs. \quad H_1: H_0 \text{ não é verdade}\]
Sob \(H_0\), \[LM_h = T \times R^2 \sim \chi^2_h,\] em que \(T\) é o tamanho da série e \(R^2\) é o coeficiente de determinação da regressão.
\[H_0: \beta_1 = \beta_2 = \beta_3 = 0 \quad vs. \quad H_1: H_0 \text{ não é verdade}\]
Code
library(lmtest)e <-augment(fit)$.innov[-c(1,2)]bgtest(e ~lag(e, 1) +lag(e, 2) +lag(e, 3), order =3, type ="Chisq")
Breusch-Godfrey test for serial correlation of order up to 3
data: e ~ lag(e, 1) + lag(e, 2) + lag(e, 3)
LM test = 4.2014, df = 3, p-value = 0.2405
Não rejeitamos \(H_0\)
Diagnóstico
Teste ARCH-LM
Serve para identificar sinais de heterocedasticidade condicional. Consiste em regredir os resíduos ao quadrado com seus valores defasados: \[\hat{\epsilon}_t^2 = \beta_1 \hat{\epsilon}_{t-1}^2 + \cdots + \beta_h \hat{\epsilon}_{t-h}^2 + u_t.\]
\[H_0: \beta_1 = \beta_2 = \cdots = \beta_h = 0 \quad vs. \quad H_1: H_0 \text{ não é verdade}\]
Sob \(H_0\), \[ARCH-LM_h = T \times R^2 \sim \chi^2_h,\] em que \(T\) é o tamanho da série e \(R^2\) é o coeficiente de determinação da regressão.
\[H_0: \beta_1 = \beta_2 = \beta_3 = 0 \quad vs. \quad H_1: H_0 \text{ não é verdade}\]
Code
e2 <-augment(fit)$.innov[-c(1,2)]^2bgtest(e2 ~lag(e2, 1) +lag(e2, 2) +lag(e2, 3), order =3, type ="Chisq")
Breusch-Godfrey test for serial correlation of order up to 3
data: e2 ~ lag(e2, 1) + lag(e2, 2) + lag(e2, 3)
LM test = 5.4761, df = 3, p-value = 0.1401
Não rejeitamos \(H_0\).
Code
augment(fit) |>features(.innov, stat_arch_lm, lag =3)
Na prática, os valores dos parâmetros são desconhecidos e precisam ser estimados.
Mão na massa
Este exercício constiste em analisar duas séries temporais passando por todo o processo visto até aqui: (EDA, identificação, estimação, diagnostico e previsão).
