Suavização Exponencial

ME607 - Séries Temporais

Prof. Carlos Trucíos
ctrucios@unicamp.br

Instituto de Matemática, Estatística e Computação Científica (IMECC),
Universidade Estadual de Campinas (UNICAMP).

Introdução

Introdução

  • Uma das limitações dos termos de tendência utilizados nos modelos de regressão é que raramente encontramos séries com tendência determinística (linear, quadrática, cúbica) na vida real.
  • Uma alternativa a este problema é utilizar splines. Contudo, seu uso para fins de previsão é bastante limitado, pois não sabemos quantas observações passadas utilizar para estimar/predizer o valor futuro da série.
  • Para superar estas limitações, surgiram os modelos de suavização exponencial. A ideia principal destes modelos é permitir com que as últimas observações da série tenham um maior peso nas previsões do que as observações mais antigas.
  • Na aula de hoje veremos alguns dos métodos de suavização exponencial mais conhecidos.

Médias Móveis

Médias Móveis Simples

Médias Móveis

Com fins de suavização (como utilizado no capítulo de decomposição):

\[\hat{Y}_t = \dfrac{Y_{t - \frac{m - 1}{2}} + \cdots + Y_t + \cdots + Y_{t + \frac{m - 1}{2}}}{m}\]

Se alterarmos a fórmula para, em lugar de considerar ambos os lados ao redor de \(Y_t\), considerar apenas as últimas \(m\) observações, temos:

\[\hat{Y}_t = \dfrac{Y_{t - m + 1} + \cdots + Y_{t - 1} + Y_t}{m}\]

Médias Móveis Simples

Dado que, MM utiliza a informação até o tempo T, como podemos utilizar MM para fazer previsão?

Médias Móveis Simples

Para fazermos a previsão através do método de MM, utilizamos a média das passadas \(m\) observações.

\[\hat{Y}_{T+1 | T} = \dfrac{Y_{T - m + 1} + \cdots + Y_{T - 1} + Y_T}{m}\]

\[\hat{Y}_{T+2 | T} = \dfrac{Y_{T - m + 2} + \cdots + Y_{T} + \hat{Y}_{T+1|T}}{m}\]

Fazer previsão com MM é recomendado quando a série não apresenta componentes de tendência e sazonalidade.

Médias Móveis Ponderadas

Uma extensão do método de MM, com a diferença de que não todas as observações tem o mesmo pesso.

\[Y_{T+h|T} = \omega_1 Y_{T + h - m} + \cdots + \omega_nY_{T + h - 1},\] Se \(T + k > T\), então \(Y_{T + k} = \hat{T}_{T + k | T}\).

MMP permite que as últimas observações recebam pesso maior na previsão. Ademais, MMP permite lidar com padrões sazonais (mas não com tendência).

Suavização Exponencial Simples

Suavização Exponencial Simples

  • Conceitualmente semelhante a Médias Móveis.
  • MM utiliza apenas \(m\) observações enquanto que SES utiliza todas as observações.
  • Apropriado quando a série não tem tendência nem sazonalidade.
  • Utiliza uma técnica de média ponderada, mas os pessos tem decaimento exponencial (daí o nome de suavização exponencial) dando maior pesso às observações mais recentes.

Suavização Exponencial Simples

Code 
library(fpp3)
algeria_economy <- global_economy %>%
  filter(Country == "Algeria")
algeria_economy %>%
  autoplot(Exports) +
  labs(y = "% of GDP", title = "Exports: Algeria")

Com este método, a previsão um passo à frente é obtida através de:

\[\hat{y}_{T+1|T} = \alpha y_{T} + (1-\alpha) \hat{y}_{T|T-1} = \hat{y}_{T|T-1} + \alpha (y_T - \hat{y}_{T|T-1}),\] em que \(0 \leq \alpha \leq 1\) é o parâmetro de suavização.

Suavização Exponencial Simples

\[\hat{y}_{T+1|T} = \alpha y_T + (1-\alpha) \underbrace{\hat{y}_{T|T-1}}_{\alpha y_{T-1} + (1-\alpha) \hat{y}_{T - 1|T-2}}\]

\[\hat{y}_{T+1|T} = \alpha y_T + \alpha (1-\alpha)y_{T-1} + (1-\alpha)^2 \underbrace{\hat{y}_{T-1|T-2}}_{\alpha y_{T-2} + (1-\alpha) \hat{y}_{T-2|T-3}}\]

\[\hat{y}_{T+1|T} = \alpha y_{T} + \alpha (1-\alpha) y_{T-1} + \alpha (1-\alpha)^2 y_{T-2} + \ldots,\]

\[\hat{y}_{T+1|T} = \alpha [y_{T} + (1-\alpha) y_{T-1} + (1-\alpha)^2 y_{T-2} + \ldots],\]

Note que \((1 + (1 - \alpha) + (1-\alpha)^2+ \cdots) = 1/\alpha\). Ou seja, a previsão \(\hat{y}_{T+1|T}\) é uma média ponderada (com pesos que somam 1) das observações passadas, em que, as observações mais recentes recebem maior peso.

Suavização Exponencial Simples

Code 
library(ggplot2)
p <- 0:100
alpha <- c(0.05, 0.2, 0.4, 0.6, 0.8, 0.95)
y1 <- alpha[1] * (1 - alpha[1])^p 
y2 <- alpha[2] * (1 - alpha[2])^p 
y3 <- alpha[3] * (1 - alpha[3])^p 
y4 <- alpha[4] * (1 - alpha[4])^p 
y5 <- alpha[5] * (1 - alpha[5])^p 
y6 <- alpha[6] * (1 - alpha[6])^p 
dados <- data.frame(Pesos = c(y1, y2, y3, y4, y5, y6),
                    Alpha = c(rep("0.05", 101), rep("0.2", 101),
                    rep("0.4", 101), rep("0.6", 101), 
                    rep("0.8", 101), rep("0.95", 101)),
                    Tempo = rep(1:101, 6))
ggplot(dados) + geom_line(aes(x = Tempo, y = Pesos, color = Alpha))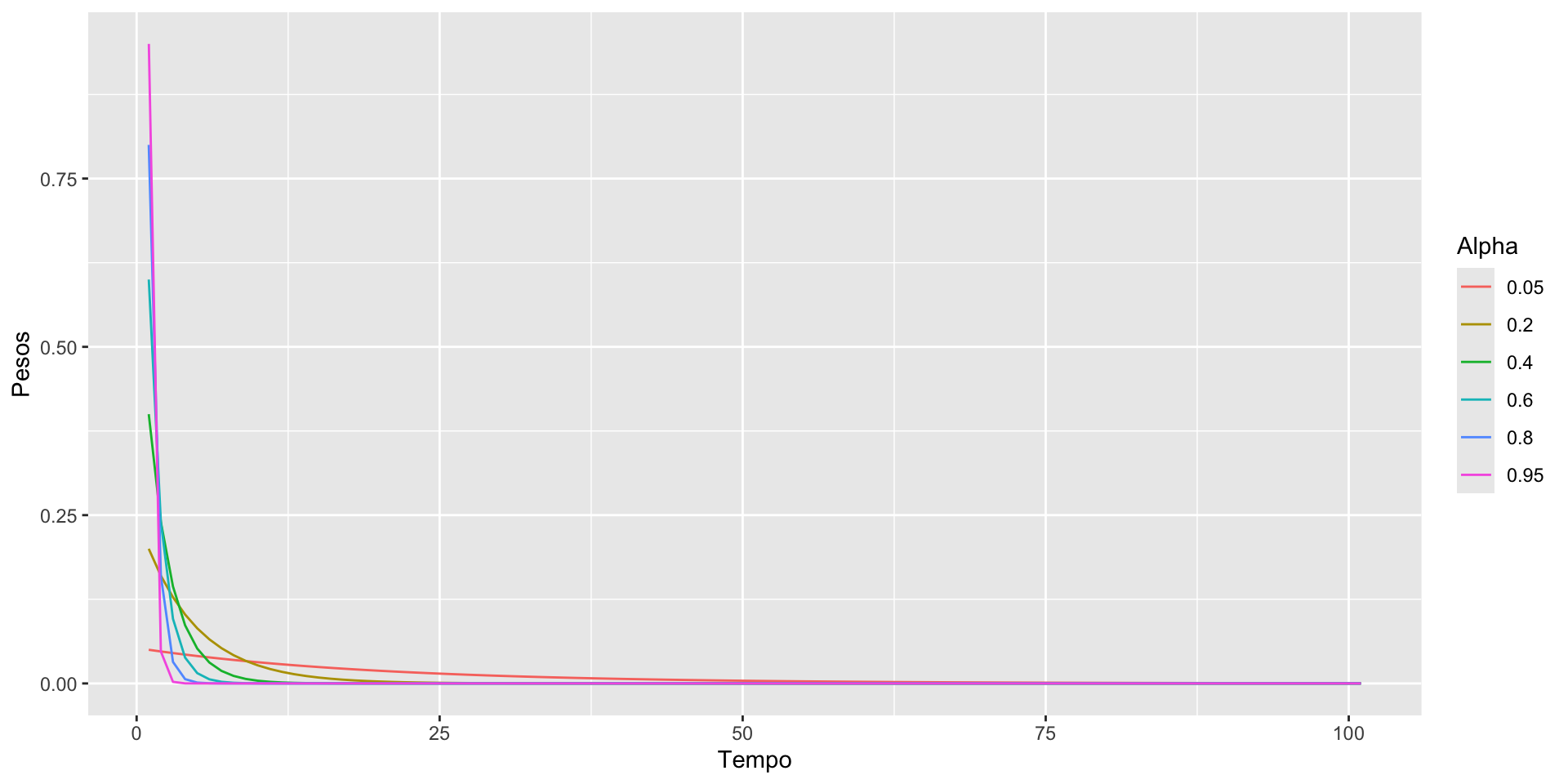

O peso que recebem as observações mais antigas cai rapidamente.

Suavização Exponencial Simples

\[\hat{y}_{T+1|T} = \alpha y_{T} + \alpha (1-\alpha) y_{T-1} + \alpha (1-\alpha)^2 y_{T-2} + \ldots,\]

  • Se \(\alpha = 1\), o método se reduz ao método NAIVE, \(\hat{y}_{T+1|T} = y_T\).
  • A medida que \(\alpha \rightarrow 1\), as observações mais recentes recebem um peso maior.
  • Na prática, não podemos utilizar uma soma infinita mas teremos: \[\hat{y}_{T+1|T} = \alpha y_{T} + \alpha (1-\alpha) y_{T-1} + \alpha (1-\alpha)^2 y_{T-2} + \cdots + \alpha (1 - \alpha)^{T-1} \hat{y}_2,\] em que \(\hat{y}_2 = \alpha y_1 + (1 - \alpha)\underbrace{\hat{y_1}}_{l_0}.\)

Suavização Exponencial Simples

\[\hat{y}_{T+1|T} = \alpha y_{T} + \alpha (1-\alpha) y_{T-1} + \alpha (1-\alpha)^2 y_{T-2} + \cdots + \alpha (1 - \alpha)^{T-1} \hat{y}_2.\]

Note que,

  • \(\hat{y}_{T+1|T} = \alpha y_T + (1-\alpha) \hat{y}_{T|T-1},\)
  • \(\hat{y}_{T|T-1} = \alpha y_{T-1} + (1-\alpha) \hat{y}_{T-1|T-2},\)
  • \(\vdots\)
  • \(\hat{y}_{3|2} = \alpha y_2 + (1-\alpha) \hat{y}_{2|1},\)
  • \(\hat{y}_{2|1} = \alpha y_1 + (1-\alpha) l_0,\)

Embora \(l_0\) e \(\alpha\) podem ser especificados pelo usuário, a prática comum é estimá-los.

Suavização Exponencial Simples

Para obter os valores estimados \(\hat{\alpha}\) e \(\hat{l}_0\), buscamos os valores que minimizem a soma de quadrados dos resíduos, ou seja:

\[SQE = \displaystyle \sum_{t=1}^T (\underbrace{y_t - \hat{y}_{t|t-1}}_{e_t})^2 = \sum_{t=1}^T e_t^2\]

Infelizmente, a solução não tem forma fechada e precisaremos de métodos numéricos para encontrá-la. Na pratica, isto não será problema, utilizaremos a função ETS() ou ses() do R para ajustar o modelo.

Não é dificil escrever um código para resolver o problema de minimização acima. Explore a função optim() do R (lhe sera muito útil no futuro) e tente fazer você mesmo.

Suavização Exponencial Simples

Code 
library(forecast)
library(TSstudio)
head(Coffee_Prices)
           Robusta Arabica
Jan 1960 0.6968643  0.9409
Feb 1960 0.6887074  0.9469
Mar 1960 0.6887074  0.9281
Apr 1960 0.6845187  0.9303
May 1960 0.6906915  0.9200
Jun 1960 0.6968643  0.9123
Code 
robusta <- Coffee_Prices[, 1]
robusta
           Jan       Feb       Mar       Apr       May       Jun       Jul
1960 0.6968643 0.6887074 0.6887074 0.6845187 0.6906915 0.6968643 0.6906915
1961 0.6765823 0.6765823 0.6684254 0.6644572 0.6622526 0.6664412 0.6684254
1962 0.6684254 0.6684254 0.6704095 0.6743777 0.6723936 0.6723936 0.6765823
1963 0.6521116 0.6137521 0.6157362 0.6157362 0.6117679 0.6117679 0.6157362
1964 0.7008326 0.7211145 0.7797561 0.8161315 0.8284771 0.8465545 0.8183361
1965 0.6283022 0.6371205 0.5798017 0.5469536 0.4872098 0.6130906 0.7162645
1966 0.8015813 0.7577103 0.7438216 0.7605763 0.7652059 0.7409557 0.7290510
1967 0.7056826 0.7286101 0.7257441 0.7471284 0.7702765 0.7824016 0.7407352
1968 0.7596945 0.7566082 0.7548445 0.7533013 0.7550649 0.7566082 0.7497740
1969 0.7065644 0.7081076 0.6871642 0.6589457 0.6496865 0.6772437 0.6871642
1970 0.8619865 0.8474364 0.8679388 0.9129121 0.9400282 0.9298873 0.9424534
1971 0.9298873 0.9296668 0.9406896 0.9400282 0.9400282 0.9340759 0.9283440
1972 0.9296668 0.9307690 0.9495080 0.9627353 0.9647195 0.9625149 1.0438630
1973 1.0540050 1.0919230 1.1097800 1.0775930 1.0745070 1.0775930 1.0581930
1974 1.2266220 1.3348670 1.3827060 1.4115860 1.4226080 1.3624240 1.3035620
1975 1.1975220 1.1549740 1.0943480 1.0809000 1.0476110 1.0877340 1.2936410
1976 1.7444760 1.8222970 1.8159040 2.3763050 2.6816380 2.8672630 2.7841500
1977 4.7676010 5.4313970 6.7479660 6.8835470 5.9426360 4.9386760 4.3317580
1978 3.9049530 3.8482960 3.4752830 3.1922160 3.0001980 3.3319850 2.7897260
1979 2.9377000 2.9211000 2.9809000 3.1262000 3.2558000 4.1621000 4.3241000
1980 3.5713000 3.5521000 3.7225000 3.6464000 3.8848000 3.7613000 3.2809000
1981 2.6283000 2.4886000 2.4723000 2.4507000 2.3477000 1.8583000 1.9357000
1982 2.3076000 2.5168000 2.4685000 2.3455000 2.2822000 2.2408000 2.1678000
1983 2.7450000 2.6846000 2.6727000 2.6727000 2.7152000 2.6511000 2.6469000
1984 2.9306000 3.0049000 3.0433000 3.0325000 3.2293000 3.1650000 3.0402000
1985 2.7675000 2.7011000 2.7079000 2.7020000 2.6685000 2.6497000 2.3433000
1986 3.7516000 3.5721000 3.7229000 3.4703000 3.1416000 2.7602000 2.7761000
1987 2.4996000 2.4269000 2.1570000 2.2290000 2.3281000 2.1615000 2.0388000
1988 2.2511000 2.2702000 2.1817000 2.1204000 2.0737000 2.0608000 1.8810000
1989 2.2342000 2.1191000 2.0810000 2.0110000 2.0133000 1.8464000 1.4383000
1990 1.0907000 1.1036000 1.2292000 1.2335000 1.1821000 1.1171000 1.1039000
1991 1.1647000 1.1435000 1.1324000 1.1229000 1.0375000 1.0005000 1.0005000
1992 1.0765000 0.9385000 0.9389000 0.9118000 0.8307000 0.8195000 0.8640000
1993 1.0340000 1.0361000 1.0119000 0.9894000 1.0179000 1.0267000 1.0891000
1994 1.3093000 1.3404000 1.4265000 1.5833000 2.0933000 2.4776000 3.6155000
1995 2.8999000 2.9694000 3.2194000 3.1918000 3.1063000 2.8400000 2.6403000
1996 1.9839000 2.1361000 2.0049000 1.9989000 2.0106000 1.8984000 1.7077000
1997 1.4813000 1.6623000 1.7688000 1.7062000 2.0635000 1.9564000 1.7560000
1998 1.8389000 1.8378000 1.8120000 1.9615000 2.0005000 1.8239000 1.6984000
1999 1.8142000 1.7467000 1.6186000 1.5282000 1.4978000 1.4460000 1.3572000
2000 1.1724000 1.0772000 1.0196000 0.9800000 0.9771000 0.9409000 0.8999000
2001 0.7143000 0.6962000 0.6729000 0.6281000 0.6512000 0.6431000 0.6047000
2002 0.5029000 0.5373000 0.6415000 0.6468000 0.6243000 0.6266000 0.6305000
2003 0.9078625 0.8966190 0.8194572 0.8249688 0.8333463 0.7542005 0.7793332
2004 0.8783206 0.8168117 0.8090955 0.8018203 0.8060091 0.8789820 0.7941041
2005 0.8148276 0.9091853 1.0915074 1.1188446 1.2361304 1.3232129 1.2760341
2006 1.3975086 1.3884697 1.3139535 1.3348974 1.3245357 1.3278426 1.4217594
2007 1.7445158 1.7434135 1.6975574 1.7544366 1.8498966 2.0432418 2.0394940
2008 2.1872035 2.5452338 2.6878727 2.4535216 2.4003903 2.4546239 2.5403836
2009 1.8241026 1.7685462 1.6823455 1.6651495 1.6671336 1.6267891 1.5802716
2010 1.5449977 1.4964961 1.4826070 1.5767442 1.5566822 1.6957937 1.8798795
2011 2.2286504 2.4107520 2.6043176 2.5875625 2.6891955 2.6003493 2.4852681
2012 2.1323085 2.2471692 2.2833249 2.2443032 2.3562979 2.3302833 2.3602662
2013 2.1977857 2.2934662 2.3426292 2.2416576 2.1864367 2.0014753 2.0989516
2014 1.9341131 2.1142306 2.3230081 2.3269764 2.2705381 2.1805896 2.2440827
2015 2.1607481 2.1684642 2.0317778 2.0295732 1.9303653 1.9896695 1.9206649
2016 1.6470716 1.6323006 1.6666927 1.7676643 1.8503376 1.8946504 2.0022359
2017 2.3880444 2.3476998 2.3529909 2.2835454 2.1684642 2.2476101 2.3135282
2018 1.9543956 1.9674029 1.9440339 1.9468999 1.9563798                    
           Aug       Sep       Oct       Nov       Dec
1960 0.6988484 0.7028166 0.7067849 0.7089895 0.6968643
1961 0.6684254 0.6723936 0.6723936 0.6704095 0.6664412
1962 0.6845187 0.6946597 0.6946597 0.6926757 0.7169259
1963 0.6117679 0.6238931 0.6258772 0.6318295 0.6521116
1964 0.8183361 0.7898972 0.7738038 0.7879130 0.7636628
1965 0.7949677 0.7775516 0.8073132 0.7568286 0.7936449
1966 0.7189101 0.6995097 0.7171464 0.7200123 0.7151622
1967 0.7175872 0.7239805 0.7294920 0.7477898 0.7499944
1968 0.7475694 0.7493330 0.7400739 0.7233191 0.7094303
1969 0.7246420 0.7630014 0.8450114 0.8207611 0.8284771
1970 0.9446578 0.9387055 0.9415715 0.9159985 0.9190849
1971 0.9298873 0.9243758 0.9190849 0.9254781 0.9373828
1972 1.0405570 1.0346040 1.0368090 1.0443040 1.0529020
1973 1.0449660 1.1044890 1.1463760 1.1684220 1.1904670
1974 1.2347790 1.1887040 1.2111900 1.2270630 1.2164810
1975 1.6986200 1.6776770 1.6108790 1.5742830 1.6320430
1976 2.9157630 3.0220240 3.3487400 3.8857730 4.4964390
1977 4.4825510 4.4422070 3.8344070 3.6752370 3.7162420
1978 2.8318350 3.2385870 3.3095760 3.1803850 2.9118620
1979 4.0111000 4.2293000 4.0640000 3.9090000 3.9020000
1980 2.9496000 2.7567000 2.7242000 2.5183000 2.5505000
1981 1.9786000 1.9703000 2.1656000 2.3135000 2.2730000
1982 2.2478000 2.4092000 2.5856000 2.6943000 2.8177000
1983 2.6526000 2.6877000 2.8726000 2.8515000 2.9271000
1984 3.0990000 3.1189000 2.9787000 2.9998000 2.7992000
1985 2.3466000 2.2941000 2.4544000 2.7816000 3.3669000
1986 2.9751000 3.6062000 3.2808000 3.1337000 2.7465000
1987 2.0845000 2.1898000 2.2822000 2.3111000 2.2716000
1988 1.8001000 1.9789000 2.0744000 2.0428000 2.2151000
1989 1.3140000 1.3234000 1.1806000 1.1744000 1.1317000
1990 1.1856000 1.2280000 1.2392000 1.2231000 1.2447000
1991 0.9900000 1.0287000 1.0115000 1.1112000 1.1197000
1992 0.8565000 0.9034000 0.9742000 1.0509000 1.1202000
1993 1.2888000 1.3779000 1.2990000 1.3550000 1.3627000
1994 3.5850000 4.0297000 3.7352000 3.3803000 2.8601000
1995 2.8700000 2.5364000 2.4859000 2.4412000 2.0479000
1996 1.7465000 1.6389000 1.6076000 1.5476000 1.3902000
1997 1.6413000 1.6568000 1.6429000 1.6764000 1.8210000
1998 1.7480000 1.7593000 1.7703000 1.7672000 1.8532000
1999 1.3905000 1.3133000 1.2901000 1.3900000 1.4725000
2000 0.8433000 0.8561000 0.7967000 0.7233000 0.6698000
2001 0.5692000 0.5351000 0.5124000 0.5221000 0.5368000
2002 0.6146000 0.7072000 0.7348000 0.8358000 0.8391000
2003 0.8002770 0.8234256 0.7910177 0.7519958 0.7914586
2004 0.7475866 0.7548619 0.6982032 0.7211312 0.8095365
2005 1.1457410 1.0333054 1.0478559 1.1342770 1.2431852
2006 1.6223799 1.6999825 1.6572129 1.6929277 1.6902822
2007 1.9277197 2.0454464 2.0084088 2.0412577 2.0148022
2008 2.4815203 2.3232286 1.9570412 2.0009131 1.8190320
2009 1.5950426 1.6274505 1.6206162 1.5317700 1.5407207
2010 1.8227798 1.7919151 1.8798795 2.0291322 2.0743270
2011 2.4707176 2.3382200 2.1627322 2.1437725 2.1695665
2012 2.3483804 2.3137487 2.3031665 2.1532524 2.1294425
2013 2.0725833 1.9351419 1.8452669 1.7572186 1.9376405
2014 2.2101315 2.2160840 2.3082371 2.2720814 2.1973448
2015 1.8911230 1.7967653 1.8249844 1.8020564 1.7478227
2016 2.0236207 2.1358359 2.2850886 2.2866319 2.2454055
2017 2.3042688 2.1865421 2.1691256 2.0134794 1.9310267
2018
Code 
ts_plot(robusta, title = "The Robusta Coffee Monthly Prices", Ytitle = "Price in USD", Xtitle = "Year")
Code 
robusta_par <- ts_split(robusta, sample.out = 12)
train <- robusta_par$train
test <- robusta_par$test
fore_ses <- ses(train, h = 12,  alpha = 0.8, initial = "simple")
fore_ses_opt <- ses(train, h = 12, initial = "optimal")
Code 
fore_ses$model
Simple exponential smoothing 

Call:
ses(y = train, h = 12, initial = "simple", alpha = 0.8)

  Smoothing parameters:
    alpha = 0.8 

  Initial states:
    l = 0.6969 

  sigma:  0.176
Code 
fore_ses_opt$model
Simple exponential smoothing 

Call:
ses(y = train, h = 12, initial = "optimal")

  Smoothing parameters:
    alpha = 0.9999 

  Initial states:
    l = 0.6957 

  sigma:  0.161

     AIC     AICc      BIC 
1989.646 1989.681 2003.252

Qual valor foi utilizado para \(l_0\)?

           Jan       Feb       Mar       Apr       May       Jun
1960 0.6968643 0.6887074 0.6887074 0.6845187 0.6906915 0.6968643
Code 
test_forecast(actual = robusta,
  forecast.obj = fore_ses_opt,
  test = test)

Suavização Exponencial Simples

Code 
library(fpp3)
algeria_economy <- global_economy |> 
  filter(Country == "Algeria") 
glimpse(algeria_economy)
Rows: 58
Columns: 9
Key: Country [1]
$ Country    <fct> "Algeria", "Algeria", "Algeria", "Algeria", "Algeria", "Alg…
$ Code       <fct> DZA, DZA, DZA, DZA, DZA, DZA, DZA, DZA, DZA, DZA, DZA, DZA,…
$ Year       <dbl> 1960, 1961, 1962, 1963, 1964, 1965, 1966, 1967, 1968, 1969,…
$ GDP        <dbl> 2723648552, 2434776646, 2001468868, 2703014867, 2909351793,…
$ Growth     <dbl> NA, -13.605441, -19.685042, 34.313729, 5.839413, 6.206898, …
$ CPI        <dbl> NA, NA, NA, NA, NA, NA, NA, NA, NA, 2.569025, 2.738580, 2.8…
$ Imports    <dbl> 67.14363, 67.50377, 20.81865, 36.82552, 29.43976, 25.83308,…
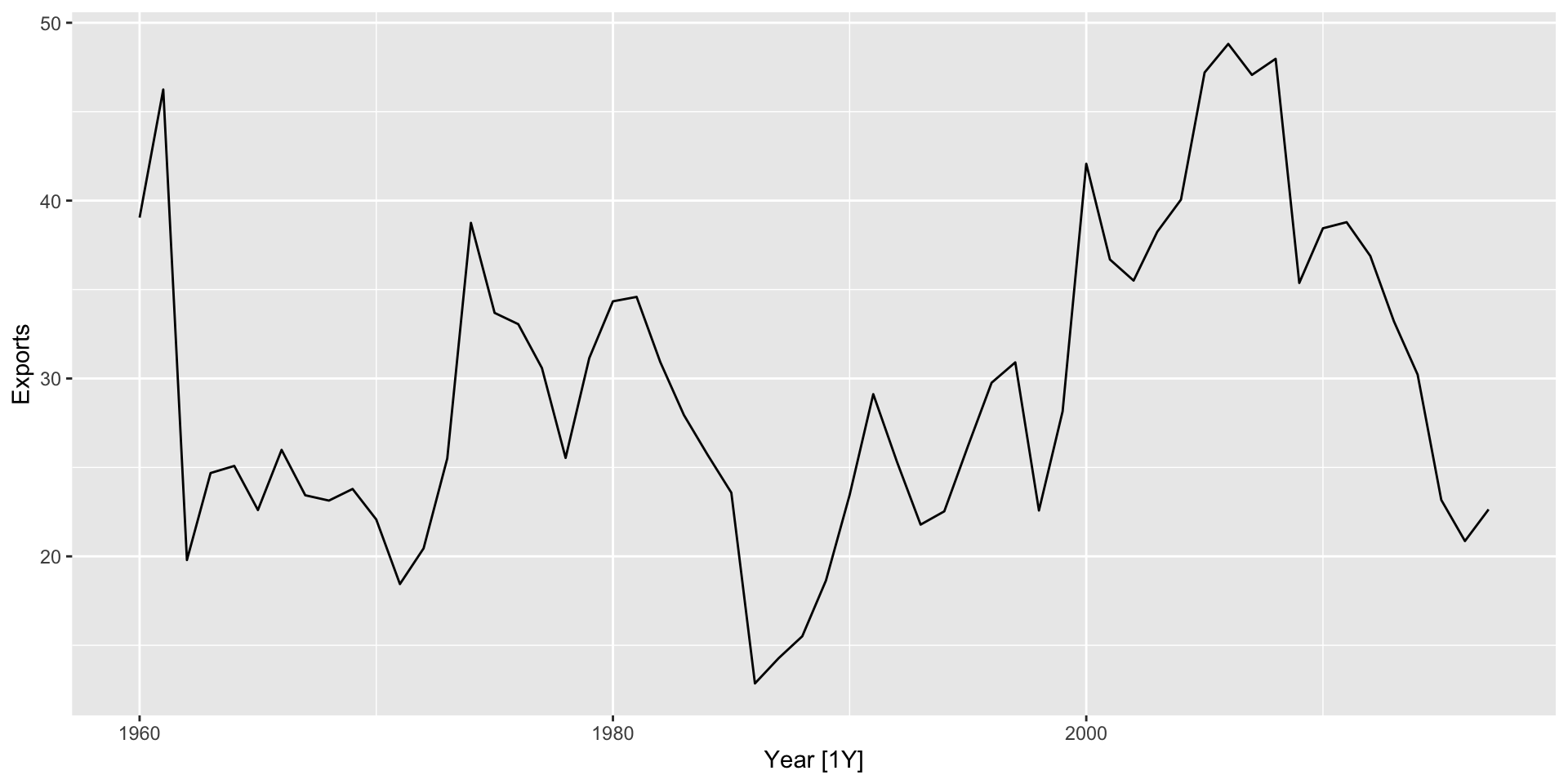
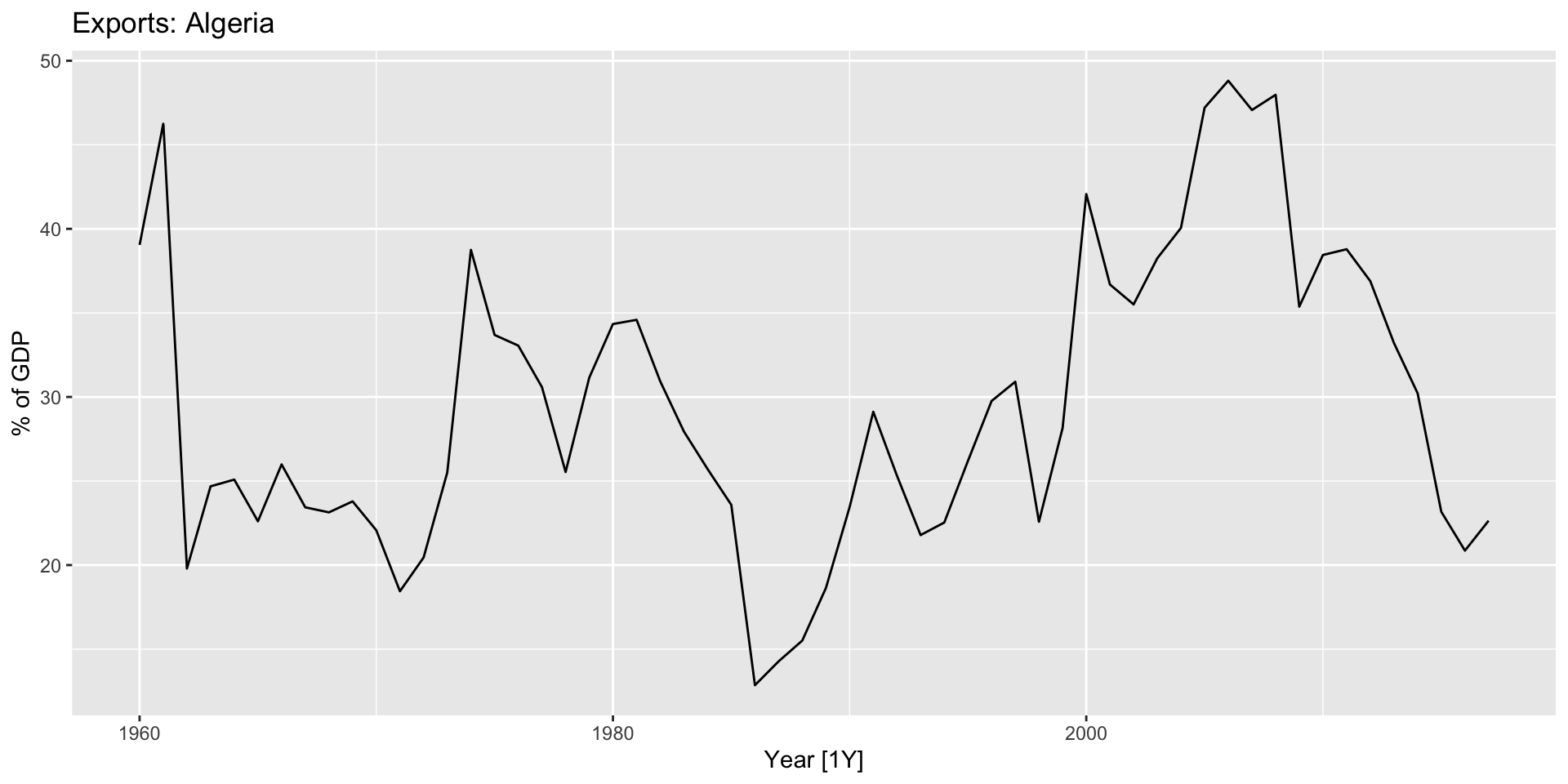
$ Exports    <dbl> 39.04317, 46.24456, 19.79387, 24.68468, 25.08406, 22.60394,…
$ Population <dbl> 11124888, 11404859, 11690153, 11985136, 12295970, 12626952,…
Code 
algeria_economy %>% autoplot(Exports)

Sem tendência nem sazonalidade claras, canditato perfeito para usar suavização exponencial.

Code 
modelo <- algeria_economy %>%
  model(ETS(Exports ~ error("A") )) # "A" para aditivo e "M" para multiplativo
report(modelo)
Series: Exports 
Model: ETS(A,N,N) 
  Smoothing parameters:
    alpha = 0.8399875 

  Initial states:
   l[0]
 39.539

  sigma^2:  35.6301

     AIC     AICc      BIC 
446.7154 447.1599 452.8968
Code 
fore_algeria <- modelo %>% forecast(h = 6)
fore_algeria
# A fable: 6 x 5 [1Y]
# Key:     Country, .model [1]
  Country .model                         Year
  <fct>   <chr>                         <dbl>
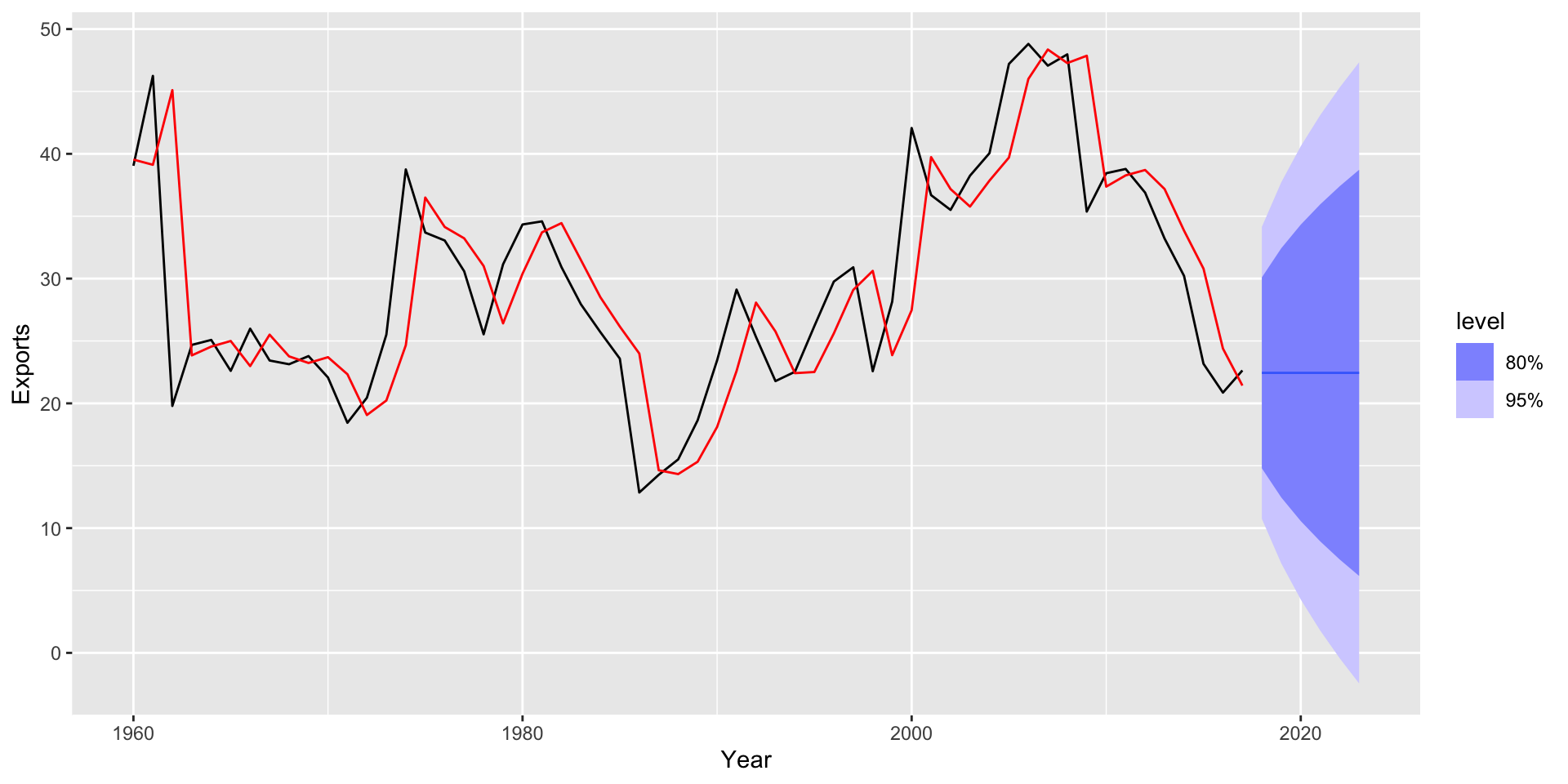
1 Algeria "ETS(Exports ~ error(\"A\"))"  2018
2 Algeria "ETS(Exports ~ error(\"A\"))"  2019
3 Algeria "ETS(Exports ~ error(\"A\"))"  2020
4 Algeria "ETS(Exports ~ error(\"A\"))"  2021
5 Algeria "ETS(Exports ~ error(\"A\"))"  2022
6 Algeria "ETS(Exports ~ error(\"A\"))"  2023
# ℹ 2 more variables: Exports <dist>, .mean <dbl>
Code 
fore_algeria %>% autoplot(algeria_economy) +
  geom_line(aes(y = .fitted), color = "red",  data = augment(modelo))

Suavização Exponencial Simples

Intuição:

Seja o processo gerador de dados da forma \[y_t = \mu_t + e_t,\] em que \(\mu_t\) é a media (não constante) de \(y_t\).

  • Seja \(\hat{\mu}_{T+1|T}\) a previsão um passo à frente do nível.
  • Como a média muda ao longo do tempo, podemos obter \(\hat{\mu}_{T+1|T}\) como a solução de \[\displaystyle \sum_{t = 1}^T (y_t - \mu_{T+1})^2\omega_t.\]
  • Derivando, temos que \(\hat{\mu}_{T+1|T} = \displaystyle \sum_{t = 1}^T y_t \omega_t.\)

Suavização Exponencial Simples

Uma forma de fazer com que as observações recentes recebam peso maior, é fazer \(\omega_t\) descrescer de forma geométrica.

  • \(\omega_T = c\), \(\omega_{T-1} = c\phi\), \(\omega_{T-2} = c\phi^2\), \(\cdots\)
  • \(1 = c(1 + \phi + \phi^2 + \phi^3+ \cdots) = \dfrac{c}{1-\phi}\)
  • \(\hat{\mu}_{T+1|T} = (1-\phi)y_T + (1-\phi)\phi y_{T-1} + (1-\phi)\phi^2 y_{T-2} + \cdots\)

Se fizermos \(1-\phi = \alpha\), temos a mesma Eq. do slide 9.

Suavização Exponencial Simples

veja que o proceso da forma \(y_t = \mu_t + e_t\) é um processo em que nem a tendência nem a sazonalidade são aparentes.

Code 
n <- 1000
e <- rnorm(n, 0, 5)
mu <- runif(n, -10, 10)
y <- mu + e
ts.plot(y)

Suavização Exponencial Simples tem previsão “flat”, i.e. \[\hat{y}_{T+h|T} = \hat{y}_{T+1|T} = \alpha y_T + (1 - \alpha) \hat{y}_{T|T-1}\]

Método de Holt

Método de Holt

  • Também conhecido como suavização exponencial dupla.
  • É uma extensão do SES.
  • Baseia-se na ideia de estimar o nível (a média) e a tendência através de dois parâmetros de suavização.

\[\hat{Y}_{T+h|T} = L_T + hT_T\]

  • Nível: \(L_T = \alpha Y_T + (1 - \alpha) (L_{T-1} + T_{T - 1})\)
  • Tendência: \(T_T = \beta(L_T - L_{T - 1}) + (1 - \beta) T_{T-1}\)
  • Número de passos à frente: \(h\)

Método de Holt

Como no caso do SES, a recursão não pode ser infinita. Assim:

  • \(L_2 = \alpha Y_1 + (1 - \alpha) (L_1 + T_1)\)
  • \(T_2 = \beta (L_2 - L_1) + (1 - \beta) T_1\)
Além do \(\alpha\) e \(\beta\), \(L_1\) e \(T_1\) também precisam ser estimados.

No R

As funções holt() do pacote forecast e ETS() do pacote fable implementam o método de Holt e já calcula os valores initicias de \(L_1\) e \(T_1\), bem como \(\alpha\) e \(\beta\).

Método de Holt

  • Utilizado quando a série apresenta tendência.
  • A previsão envolve duas equações de suavização: uma para o nível e outra para a tendência:
    • \(\text{Previsão: } \quad \hat{Y}_{T+h|T} = L_T + hT_T,\)
    • \(\text{Equação do Nível: } L_T = \alpha Y_T + (1 - \alpha) (L_{T-1} + T_{T - 1})\)
    • \(\text{Equação de Tendência: } \quad T_T = \beta(L_T - L_{T - 1}) + (1 - \beta) T_{T-1}\)

Em que \(0 \leq \alpha, \beta \leq 1\). Ademais, note que no instante \(T=2\) precisaremos de \(L_1\) e \(T_1\)

Para estimar os parâmetros, minimizamos a soma de quadrados dos resíduos.

Método de Holt

Code 
australia_economy <- global_economy |> 
  filter(Country == "Australia") |> 
  mutate(Pop = Population / 1e6) # População em milhoes 1e6 = 10^6
glimpse(australia_economy)
Rows: 58
Columns: 10
Key: Country [1]
$ Country    <fct> "Australia", "Australia", "Australia", "Australia", "Austra…
$ Code       <fct> AUS, AUS, AUS, AUS, AUS, AUS, AUS, AUS, AUS, AUS, AUS, AUS,…
$ Year       <dbl> 1960, 1961, 1962, 1963, 1964, 1965, 1966, 1967, 1968, 1969,…
$ GDP        <dbl> 18573188487, 19648336880, 19888005376, 21501847911, 2375853…
$ Growth     <dbl> NA, 2.4856050, 1.2964777, 6.2142784, 6.9787237, 5.9834500, …
$ CPI        <dbl> 7.960458, 8.142560, 8.116545, 8.168574, 8.402706, 8.688866,…
$ Imports    <dbl> 14.06175, 15.02508, 12.63093, 13.83405, 13.76450, 15.26734,…
$ Exports    <dbl> 12.99445, 12.40310, 13.94301, 13.00589, 14.93825, 13.22018,…
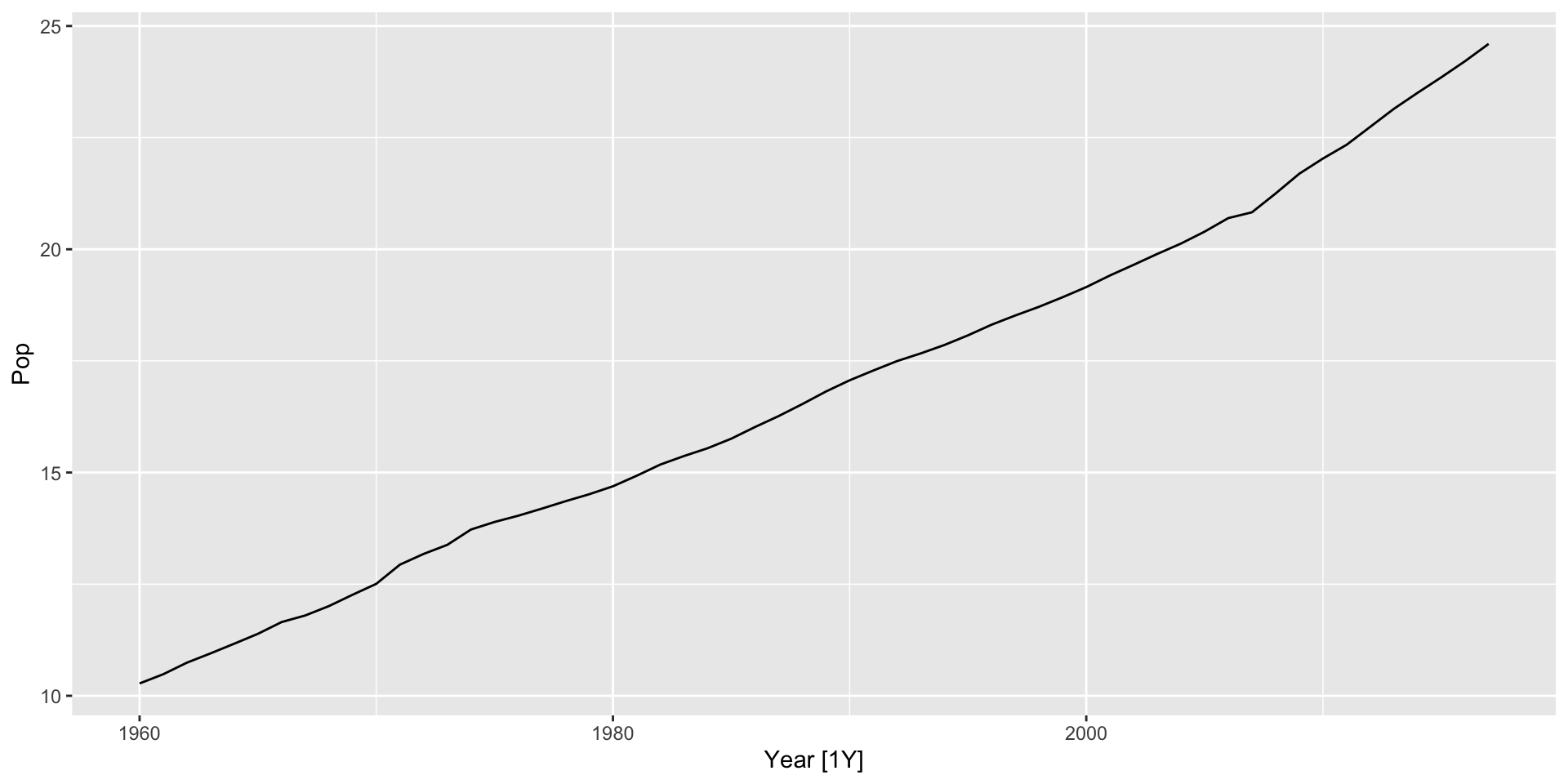
$ Population <dbl> 10276477, 10483000, 10742000, 10950000, 11167000, 11388000,…
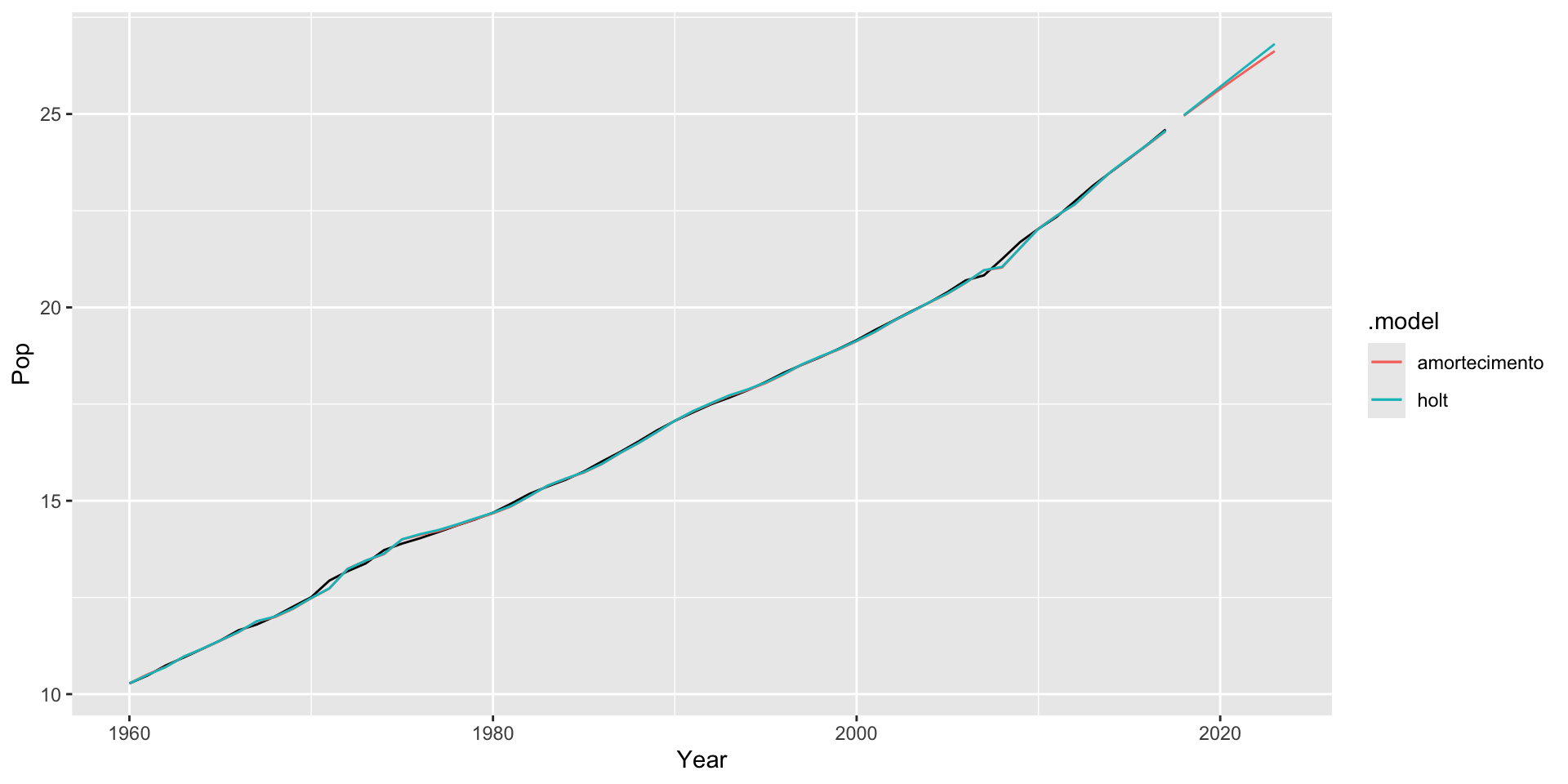
$ Pop        <dbl> 10.27648, 10.48300, 10.74200, 10.95000, 11.16700, 11.38800,…
Code 
australia_economy %>% autoplot(Pop)

Tendência evidente.

Code 
modelo <- australia_economy %>%
  model(ETS(Pop ~ error("A") + trend("A")))
report(modelo)
Series: Pop 
Model: ETS(A,A,N) 
  Smoothing parameters:
    alpha = 0.9999 
    beta  = 0.3266366 

  Initial states:
     l[0]      b[0]
 10.05414 0.2224818

  sigma^2:  0.0041

      AIC      AICc       BIC 
-76.98569 -75.83184 -66.68347
Code 
fore_aus <- modelo %>% forecast(h = 6)
fore_aus
# A fable: 6 x 5 [1Y]
# Key:     Country, .model [1]
  Country   .model                                    Year
  <fct>     <chr>                                    <dbl>
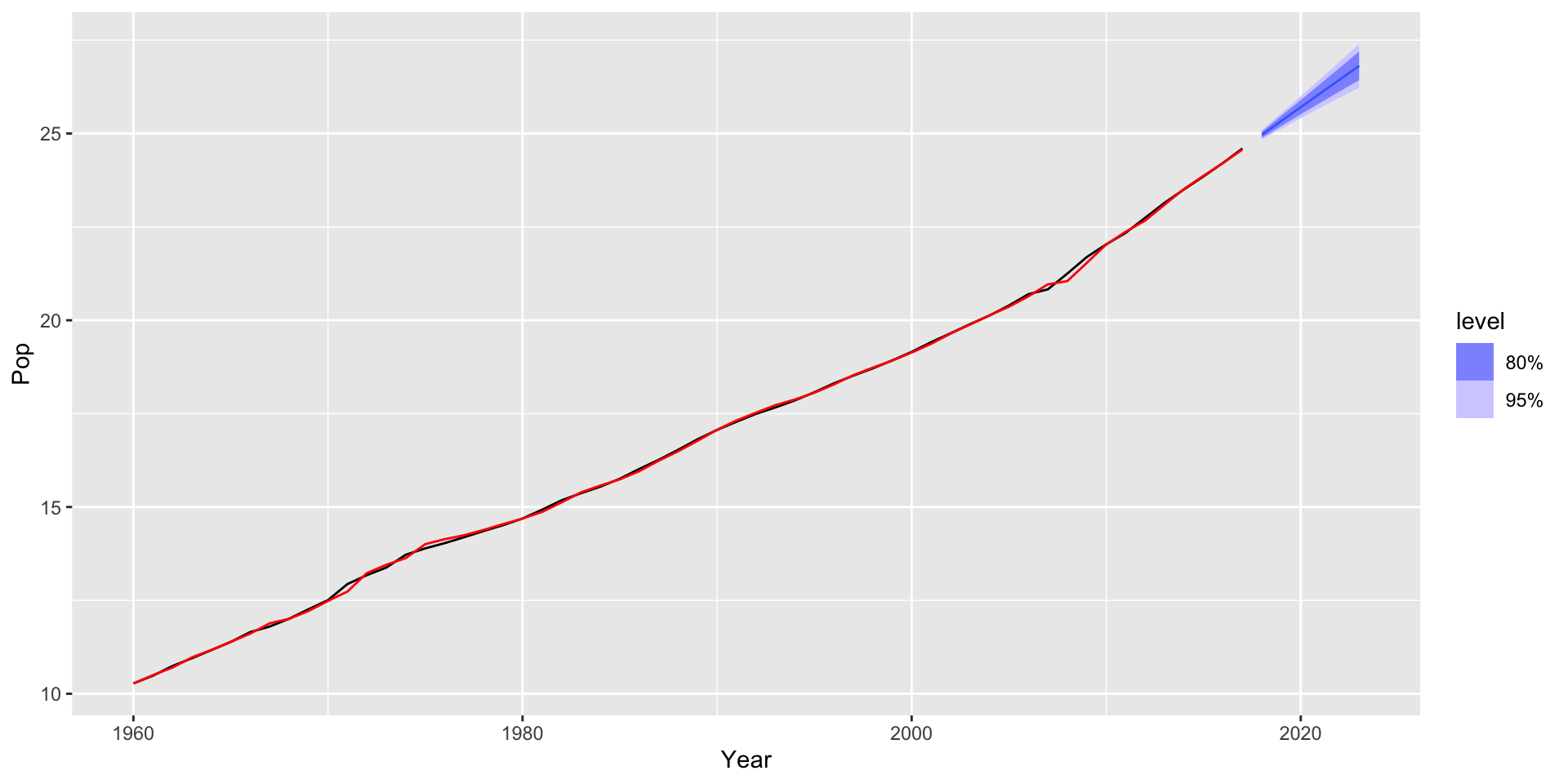
1 Australia "ETS(Pop ~ error(\"A\") + trend(\"A\"))"  2018
2 Australia "ETS(Pop ~ error(\"A\") + trend(\"A\"))"  2019
3 Australia "ETS(Pop ~ error(\"A\") + trend(\"A\"))"  2020
4 Australia "ETS(Pop ~ error(\"A\") + trend(\"A\"))"  2021
5 Australia "ETS(Pop ~ error(\"A\") + trend(\"A\"))"  2022
6 Australia "ETS(Pop ~ error(\"A\") + trend(\"A\"))"  2023
# ℹ 2 more variables: Pop <dist>, .mean <dbl>
Code 
fore_aus %>% autoplot(australia_economy) +
  geom_line(aes(y = .fitted), color = "red",  data = augment(modelo))

Code 
australia_economy_ts <- ts(australia_economy$Pop, frequency = 1, start = "1960")
#info_ts(australia_economy_ts)
fore_holt <- holt(australia_economy_ts, h = 6, initial = "optimal")
fore_holt$model
Holt's method 

Call:
holt(y = australia_economy_ts, h = 6, initial = "optimal")

  Smoothing parameters:
    alpha = 0.9999 
    beta  = 0.3267 

  Initial states:
    l = 10.0541 
    b = 0.2225 

  sigma:  0.0643

      AIC      AICc       BIC 
-76.98568 -75.83184 -66.68347
Code 
fore_aus$.mean
[1] 24.96786 25.33678 25.70571 26.07464 26.44356 26.81249
Code 
fore_holt$mean
Time Series:
Start = 2018 
End = 2023 
Frequency = 1 
[1] 24.96786 25.33679 25.70572 26.07466 26.44359 26.81252

Método de Holt com amortização

  • O método de Holt (1957) assume que, para fazer a previsão, a tendência é constante nos \(h\) passos à frente.
  • Em 1985, foi proposto um método que amortece a tendência. Com este método as equações são definidas como:

\[\begin{align} \hat{y}_{T+h|T} = & L_T + (\phi + \phi^2 + \cdots + \phi^h) T_T, \\ L_T = & \alpha y_T + (1-\alpha) (L_{T-1} + \phi T_{T-1}), \\ T_T = & \beta (L_T - L_{T-1}) + (1 - \beta) \phi T_{T-1}. \end{align}\]

Note que se \(\phi = 1\) temos o método de Holt.

Método de Holt com tendência não constante

Code 
modelo <- australia_economy |> 
  model(holt = ETS(Pop ~ error("A") + trend("A")),
        amortecimento = ETS(Pop ~ error("A") + trend("Ad")))
modelo |> select(amortecimento) |> report()
Series: Pop 
Model: ETS(A,Ad,N) 
  Smoothing parameters:
    alpha = 0.9986305 
    beta  = 0.4271838 
    phi   = 0.98 

  Initial states:
     l[0]      b[0]
 10.03648 0.2478533

  sigma^2:  0.0045

      AIC      AICc       BIC 
-71.01630 -69.36924 -58.65364
Code 
fore_aus <- modelo %>% forecast(h = 6)
fore_aus
# A fable: 12 x 5 [1Y]
# Key:     Country, .model [2]
   Country   .model         Year
   <fct>     <chr>         <dbl>
 1 Australia holt           2018
 2 Australia holt           2019
 3 Australia holt           2020
 4 Australia holt           2021
 5 Australia holt           2022
 6 Australia holt           2023
 7 Australia amortecimento  2018
 8 Australia amortecimento  2019
 9 Australia amortecimento  2020
10 Australia amortecimento  2021
11 Australia amortecimento  2022
12 Australia amortecimento  2023
# ℹ 2 more variables: Pop <dist>, .mean <dbl>
Code 
fore_aus |> autoplot(australia_economy, level = NULL) +
  geom_line(aes(y = .fitted, color = .model),  data = augment(modelo))

Code 
fore_holt <- holt(australia_economy_ts, h = 6, initial = "optimal", damped = TRUE)
fore_holt$model
Damped Holt's method 

Call:
holt(y = australia_economy_ts, h = 6, damped = TRUE, initial = "optimal")

  Smoothing parameters:
    alpha = 0.9984 
    beta  = 0.4272 
    phi   = 0.98 

  Initial states:
    l = 10.0365 
    b = 0.2478 

  sigma:  0.0672

      AIC      AICc       BIC 
-71.01628 -69.36923 -58.65363
Code 
fore_aus$.mean[-c(1:6)]
[1] 24.95437 25.30277 25.64419 25.97879 26.30669 26.62803
Code 
fore_holt$mean
Time Series:
Start = 2018 
End = 2023 
Frequency = 1 
[1] 24.95437 25.30276 25.64419 25.97878 26.30669 26.62804

Método de Holt com tendência não constante

Note que, quando \(h \rightarrow \infty\), \[y_{T+h|T} = \hat{\mu}_{T|T} + (\phi + \phi^2 + \cdots + \phi^h) \hat{\beta}_T \rightarrow l_t + \dfrac{\phi}{1-\phi} \hat{\beta}_T\]

Observação

Quando a tendência é exponencial, podemos usar o argumento exponential = TRUE na função holt().

Método de Holt-Winters

Método de Holt-Winters

  • É uma extensão do método de Holt.
  • Lida com séries temporais que possuem tendência e sazonalidade.
  • Para fazer isto, inclui um terceiro parâmetro de suavização.
  • É necessário conhecer o período sazonal \(m\)

Método de Holt-Winters

Holt-Winters Aditivo

\[\hat{Y}_{T+h|T} = L_T + h T_T + S_{T + h - m (k + 1)},\]

\[L_T = \alpha (Y_T - S_{T-m}) + (1-\alpha) (L_{T-1}+ T_{T-1}),\]

\[T_T = \beta (L_T - L_{T-1}) + (1-\beta) T_{T-1},\]

\[S_T = \gamma (Y_T - L_{T-1} - T_{T-1}) + (1-\gamma) S_{T-m}.\] Em que \(k\) é a parte inteira de \((h-1)/m\).

Método de Holt-Winters

Holt-Winters Multiplicativo

\[\hat{Y}_{T+h|T} = (L_T + h T_T) S_{T+ h - m(k+1)},\]

\[L_t = \alpha \dfrac{Y_T}{S_{T - m}} + (1-\alpha) (L_{T-1} + T_{T-1}),\]

\[T_T = \beta (L_T - L_{T-1}) + (1-\beta) T_{T-1},\]

\[S_T = \gamma \dfrac{Y_T}{L_{T-1} + T_{T-1}} + (1-\gamma) S_{T-m}\]

Método de Holt-Winters

Se a variação sazonal é constante utilizamos o modelo aditivo, caso contrário o multiplicativo.

Utilizando a função ETS():

No R

Além da função ETS(), as funções HoltWinters() do pacote stats e hw() do pacote forecast implementam o método de Holt-Winters. A função hw() permite lidar com tendências exponenciais ou amortecidas.

Note que, além de \(\alpha, \beta, \gamma\) e os valores iniciais de \(L_1\) e \(T_1\), precisamos valores iniciais para \(S_1, \cdots, S_{m}\). Assim como nos casos anteriores, estes valores são obtidos minimizando a soma de quadrados dos resíduos.

Método de Holt-Winters

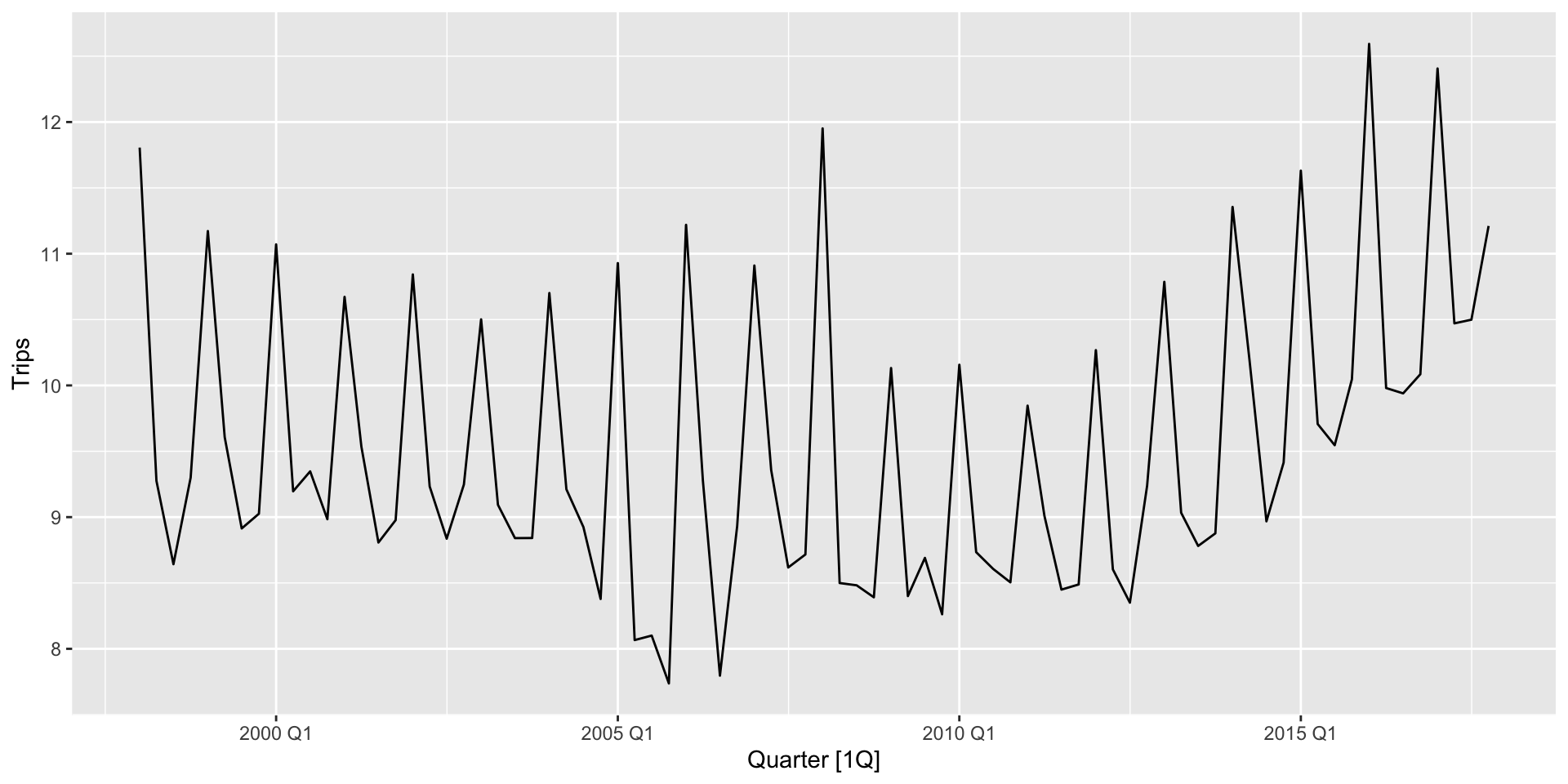
Code 
aus_holidays <- tourism %>% 
  filter(Purpose == "Holiday") %>%
  summarise(Trips = sum(Trips)/1000) # Agrupamos por Quarter e os valores unidades de mil. 
glimpse(aus_holidays)
Rows: 80
Columns: 2
$ Quarter <qtr> 1998 Q1, 1998 Q2, 1998 Q3, 1998 Q4, 1999 Q1, 1999 Q2, 1999 Q3,…
$ Trips   <dbl> 11.806038, 9.275662, 8.642489, 9.299524, 11.172027, 9.607613, …
Code 
aus_holidays %>% autoplot(Trips)

Code 
modelo <- aus_holidays |> 
  model(HWA = ETS(Trips ~ error("A") + trend("A") + season("A")),
        HWM = ETS(Trips ~ error("M") + trend("A") + season("M")))
modelo |> select(HWA) |> report()
Series: Trips 
Model: ETS(A,A,A) 
  Smoothing parameters:
    alpha = 0.2620382 
    beta  = 0.04314266 
    gamma = 0.0001000312 

  Initial states:
     l[0]       b[0]      s[0]      s[-1]      s[-2]    s[-3]
 9.791341 0.02106875 -0.534408 -0.6697662 -0.2937802 1.497954

  sigma^2:  0.1931

     AIC     AICc      BIC 
228.5676 231.1390 250.0058
Code 
modelo |> select(HWM) |> report()
Series: Trips 
Model: ETS(M,A,M) 
  Smoothing parameters:
    alpha = 0.2236926 
    beta  = 0.03042124 
    gamma = 0.0001000009 

  Initial states:
     l[0]        b[0]      s[0]     s[-1]     s[-2]    s[-3]
 10.01351 -0.01141645 0.9430572 0.9270043 0.9692079 1.160731

  sigma^2:  0.0021

     AIC     AICc      BIC 
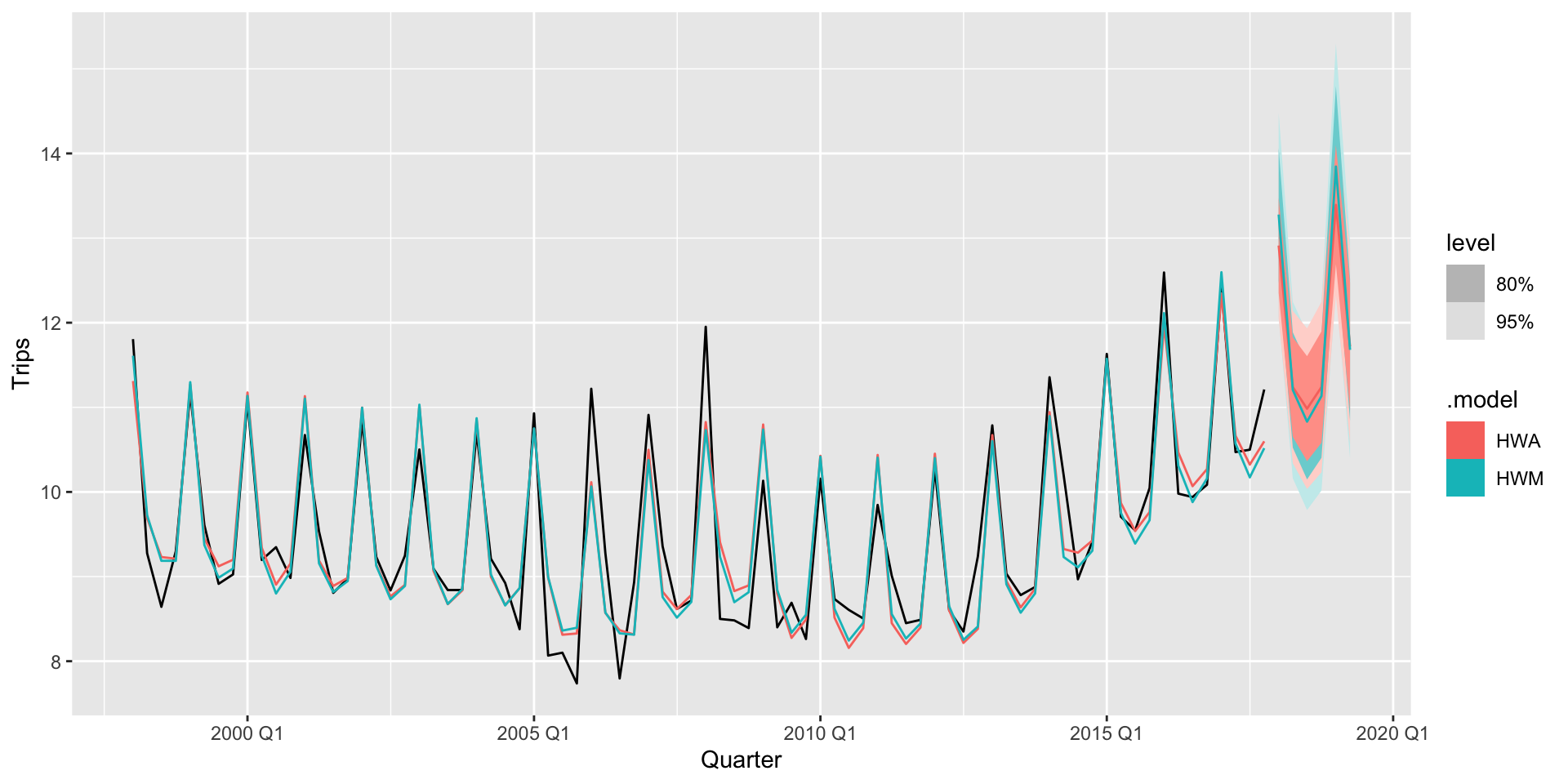
226.7196 229.2910 248.1578
Code 
fore_holidays <- modelo %>% forecast(h = 6)
fore_holidays
# A fable: 12 x 4 [1Q]
# Key:     .model [2]
   .model Quarter
   <chr>    <qtr>
 1 HWA    2018 Q1
 2 HWA    2018 Q2
 3 HWA    2018 Q3
 4 HWA    2018 Q4
 5 HWA    2019 Q1
 6 HWA    2019 Q2
 7 HWM    2018 Q1
 8 HWM    2018 Q2
 9 HWM    2018 Q3
10 HWM    2018 Q4
11 HWM    2019 Q1
12 HWM    2019 Q2
# ℹ 2 more variables: Trips <dist>, .mean <dbl>
Code 
fore_holidays |> autoplot(aus_holidays) +
  geom_line(aes(y = .fitted, color = .model), data = augment(modelo))

Método de Holt-Winters

Code 
aus_holidays_ts <- ts(aus_holidays$Trips, frequency = 4, start = c(1998, 1))
modelo_HoltWinters <- HoltWinters(aus_holidays_ts)
fore_HoltWinters <- forecast(modelo_HoltWinters, h = 6)
modelo_HoltWinters
Holt-Winters exponential smoothing with trend and additive seasonal component.

Call:
HoltWinters(x = aus_holidays_ts)

Smoothing parameters:
 alpha: 0.1998394
 beta : 0.1494321
 gamma: 0.1610995

Coefficients:
         [,1]
a  11.1700046
b   0.1134632
s1  1.6361980
s2 -0.2403544
s3 -0.6159145
s4 -0.3710807
Code 
fore_hw <- hw(aus_holidays_ts, h = 6)
fore_hw$model
Holt-Winters' additive method 

Call:
hw(y = aus_holidays_ts, h = 6)

  Smoothing parameters:
    alpha = 0.262 
    beta  = 0.0431 
    gamma = 1e-04 

  Initial states:
    l = 9.7913 
    b = 0.0211 
    s = -0.5344 -0.6698 -0.2938 1.498

  sigma:  0.4394

     AIC     AICc      BIC 
228.5676 231.1390 250.0058
Code 
fore_holidays$.mean[c(1:6)]
[1] 12.91147 11.23965 10.98369 11.23914 13.39163 11.71981
Code 
fore_HoltWinters$mean
         Qtr1     Qtr2     Qtr3     Qtr4
2018 12.91967 11.15658 10.89448 11.25278
2019 13.37352 11.61043
Code 
fore_hw$mean
         Qtr1     Qtr2     Qtr3     Qtr4
2018 12.91147 11.23964 10.98366 11.23916
2019 13.39163 11.71980

Método de Holt-Winters

Observação

A função HoltWinter() utiliza uma fórmula levemente diferente, por isso \(\alpha, \beta, \gamma\) estimados e os valores iniciais são diferentes.

  • Se quisermos incluir o amorcetimento na componente de tendência quando utilizamos ETS(), basta trocar trend("A") por trend("Ad") nos códigos do slide anterior.
  • Na função hw() basta fazer o argumento damped = TRUE

Comentários finais

  • Além dos métodos mencionados, existem vários outros métodos de suavização.
  • Esses métodos podem ser obtidos como as possíveis configurações que podem ser obtidas com:
    • error(): A (aditivo) ou M (multiplicativo)
    • season(): A, M ou N (nenhum).
    • trend(): N, A, M, Ad (aditivo amortecido), Md (multiplicativo amortecido).
  • A escolha não sempre é facil. Embora não sejam infalíveis, existem métodos automáticos (teste fazendo, por exemplo, modelo <- aus_holidays |> model(auto = ETS(Trips)).
  • Maiores detalhes a respeito do procedimento automático podem ser enconrados em Hydman et al. (2002).
  • Para um maior aprofundamento nos metodos de suavização exponencial, ver Hyndman et al. (2008). Link com código e erratas, aqui.

Referências