Rows: 198
Columns: 6
$ Quarter <qtr> 1970 Q1, 1970 Q2, 1970 Q3, 1970 Q4, 1971 Q1, 1971 Q2, 197…
$ Consumption <dbl> 0.61856640, 0.45198402, 0.87287178, -0.27184793, 1.901344…
$ Income <dbl> 1.0448013, 1.2256472, 1.5851538, -0.2395449, 1.9759249, 1…
$ Production <dbl> -2.45248553, -0.55145947, -0.35865175, -2.18569087, 1.909…
$ Savings <dbl> 5.2990141, 7.7898938, 7.4039841, 1.1698982, 3.5356669, 5.…
$ Unemployment <dbl> 0.9, 0.5, 0.5, 0.7, -0.1, -0.1, 0.1, 0.0, -0.2, -0.1, -0.…Modelos de regressão em dados de séries temporais
ME607 - Séries Temporais
ctrucios@unicamp.br
Instituto de Matemática, Estatística e Computação Científica (IMECC),
Universidade Estadual de Campinas (UNICAMP).
Introdução
Introdução
- Em ME613 estudaram modelos de regressão em um contexto de dados de corte transversal.
- Sob algumas suposições, \(\hat{\beta}\) é o melhor estimador linear não viesado.
- Dados de séries temporais se diferenciam dos dados de corte transversal em que eles tem uma ordem cronológica
- Temperatura
- PBI
- Indice da bolsa de valores de SP
- etc
- Estudaremos MRL em um contexto de séries temporais, estabeleceremos novas hipóteses e propriedades dos estimadores
Introdução
O dataset us_change do pacote fpp3 contém dados trimestrais sobre a variação percentual nas despesas de consumo, variação percentual na renda, variação percentual na produção industrial, variação percentual na poupança e a mudança na taxa de desemprego nos Estados Unidos desde 1970 até 2019.
Queremos criar um modelo da forma
\[\text{Consumption} = \beta_0 + \beta_1 \text{Income } + \beta_2 \text{Production } + \beta_3 \text{Savings } + \beta_4 \text{Unemployment } + e\]
Introdução
Code
Series: Consumption
Model: TSLM
Residuals:
Min 1Q Median 3Q Max
-0.90555 -0.15821 -0.03608 0.13618 1.15471
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.253105 0.034470 7.343 5.71e-12 ***
Income 0.740583 0.040115 18.461 < 2e-16 ***
Production 0.047173 0.023142 2.038 0.0429 *
Savings -0.052890 0.002924 -18.088 < 2e-16 ***
Unemployment -0.174685 0.095511 -1.829 0.0689 .
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.3102 on 193 degrees of freedom
Multiple R-squared: 0.7683, Adjusted R-squared: 0.7635
F-statistic: 160 on 4 and 193 DF, p-value: < 2.22e-16Aparentemente, usamos o modelo como sempre. O que mudou?
No processo de estimação, nada!. Já nas hipóteses, na interpretação dos resultados e nas conclusões, muita coisa!
Modelo de regressão em dados de séries temporais
Modelo de regressão em dados de séries temporais
Hipóteses no modelo de regressão clássico
- HRLM1: O modelo populacional é linear nos parâmetros, \(y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \ldots + \beta_k x_k + e\)
- HRLM2: \((y_1, x_{1,1}, \ldots, x_{1,k}), \cdots, (y_n, x_{n,1}, \ldots, x_{n,k})\) constituem uma a.a. de tamanho \(n\) do modelo populacional
- HRLM3: Não existe colinearidade perfeita entre as variáveis independentes e nenhuma das variáveis independentes é constante.
- HRLM4: \(E(u|X) = 0\)
- HRLM5: Os erros tem variância constante (homocedasticidade)
- HRLM6: O erro populacional \(e\) é independente das variaveis explicativas (\(X\)) e \(e \sim N(0, \sigma^2)\)
Modelo de regressão em dados de séries temporais
Hipóteses no modelo de regressão com dados de séries temporais
- HST1: \(y_t = \beta_0 + \beta_1 x_{t1} + \cdots + \beta_k x_{tk} + e_t\), \(t = 1, \ldots, n\)
- HST2: Não existe colinearidade perfeita entre as variáveis independêntes e nenhuma das variáveis independentes é constante.
- HST3: \(E(e_t|X) = 0\), \(t = 1, \ldots, n\) (implica que \(e_t\) é não correlacionado com as v. explicativas em todos os períodos de tempo)
- HST4: Homocedasticidade, \(V(e_t|X) = V(e_t) = \sigma^2\), \(t=1, \ldots, n\)
- HST5: \(Corr(e_t, e_s | X) = 0\), \(\forall t\neq s\) (sem correlação serial)
- HST6: Os erros \(e_t\) são independentes de \(X\) e \(e_t \sim N(0, \sigma^2)\)
Modelo de regressão em dados de séries temporais
Hipóteses no modelo de regressão com dados de séries temporais
- Sob HST1–HST3, \(E(\hat{\beta}) = \beta\)
- Sob HST1–HST5, \(\hat{\beta}\) é BLUE (melhor estimador linear não viesado)
- HST6, nos permite fazer inferência.
Demostração:
Modelo de regressão em dados de séries temporais

- Verificadas as novas suposições, é só aplicar regressão como sempre?
- Sim, mas deve verificar as suposições!. É muito comúm encontrarmos falsos achados quando trabalhamos com modelos de regressão em dados de séries temporais.
Modelo de regressão em dados de séries temporais
Code
Series: Consumption
Model: TSLM
Residuals:
Min 1Q Median 3Q Max
-0.90555 -0.15821 -0.03608 0.13618 1.15471
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.253105 0.034470 7.343 5.71e-12 ***
Income 0.740583 0.040115 18.461 < 2e-16 ***
Production 0.047173 0.023142 2.038 0.0429 *
Savings -0.052890 0.002924 -18.088 < 2e-16 ***
Unemployment -0.174685 0.095511 -1.829 0.0689 .
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.3102 on 193 degrees of freedom
Multiple R-squared: 0.7683, Adjusted R-squared: 0.7635
F-statistic: 160 on 4 and 193 DF, p-value: < 2.22e-16Code
library(ggplot2)
augment(modelo) |> select(Quarter, Consumption, .fitted) |>
pivot_longer(cols = c("Consumption", ".fitted"), values_to = "values", names_to = "serie") |> ggplot() +
geom_line(aes(x = Quarter, y = values, color = serie)) +
ggtitle("Variação percentual nas despesas de consumo USA. Período 1970.Q1 -- 2019.Q2")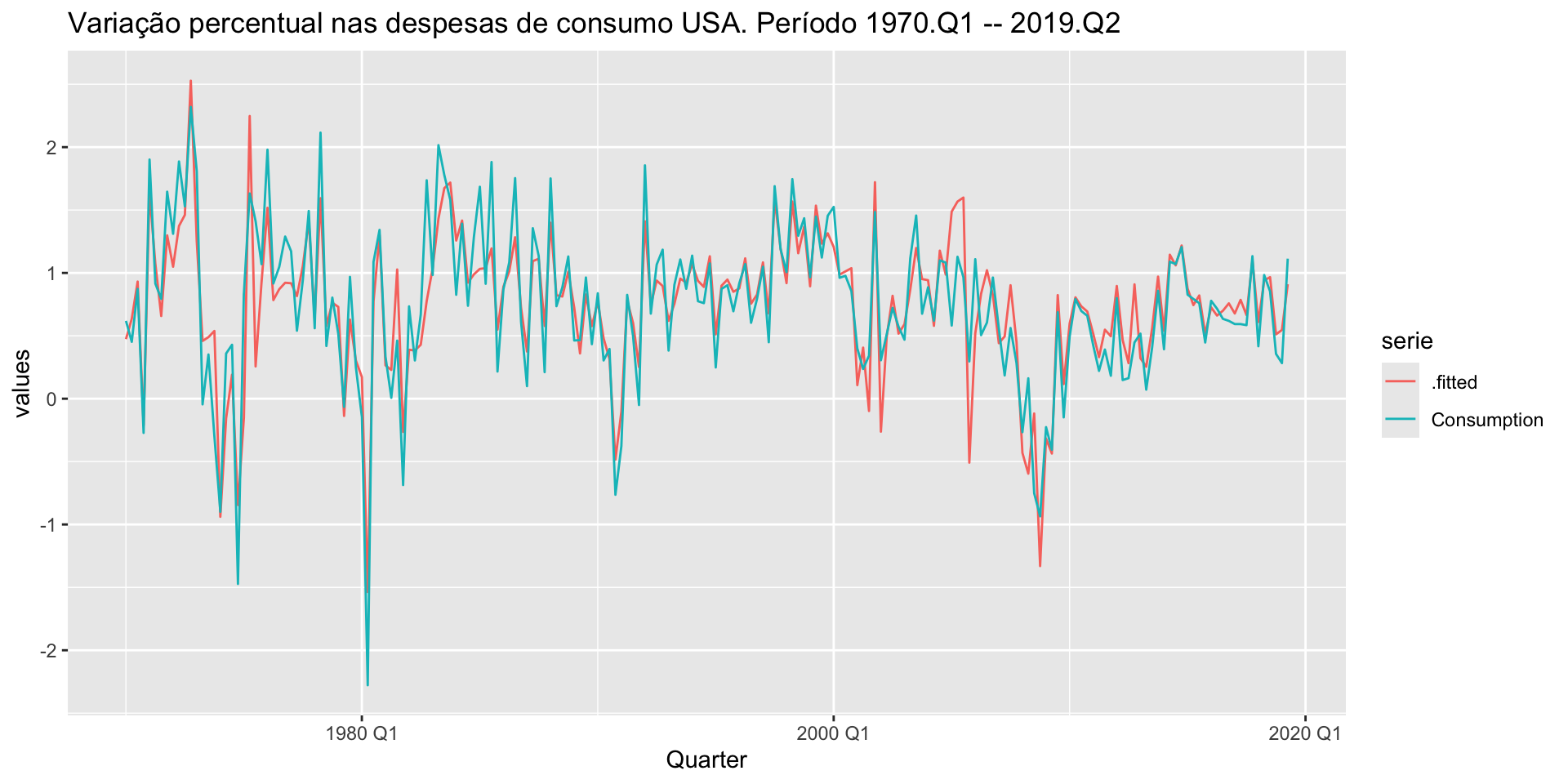
# A tibble: 5 × 6
.model term estimate std.error statistic p.value
<chr> <chr> <dbl> <dbl> <dbl> <dbl>
1 TSLM(Consumption ~ Income + Produ… (Int… 0.253 0.0345 7.34 5.71e-12
2 TSLM(Consumption ~ Income + Produ… Inco… 0.741 0.0401 18.5 1.65e-44
3 TSLM(Consumption ~ Income + Produ… Prod… 0.0472 0.0231 2.04 4.29e- 2
4 TSLM(Consumption ~ Income + Produ… Savi… -0.0529 0.00292 -18.1 2.03e-43
5 TSLM(Consumption ~ Income + Produ… Unem… -0.175 0.0955 -1.83 6.89e- 2# A tibble: 1 × 3
.model bp_stat bp_pvalue
<chr> <dbl> <dbl>
1 TSLM(Consumption ~ Income + Production + Savings + Unemploy… 16.5 0.000879# A tibble: 1 × 3
.model lb_stat lb_pvalue
<chr> <dbl> <dbl>
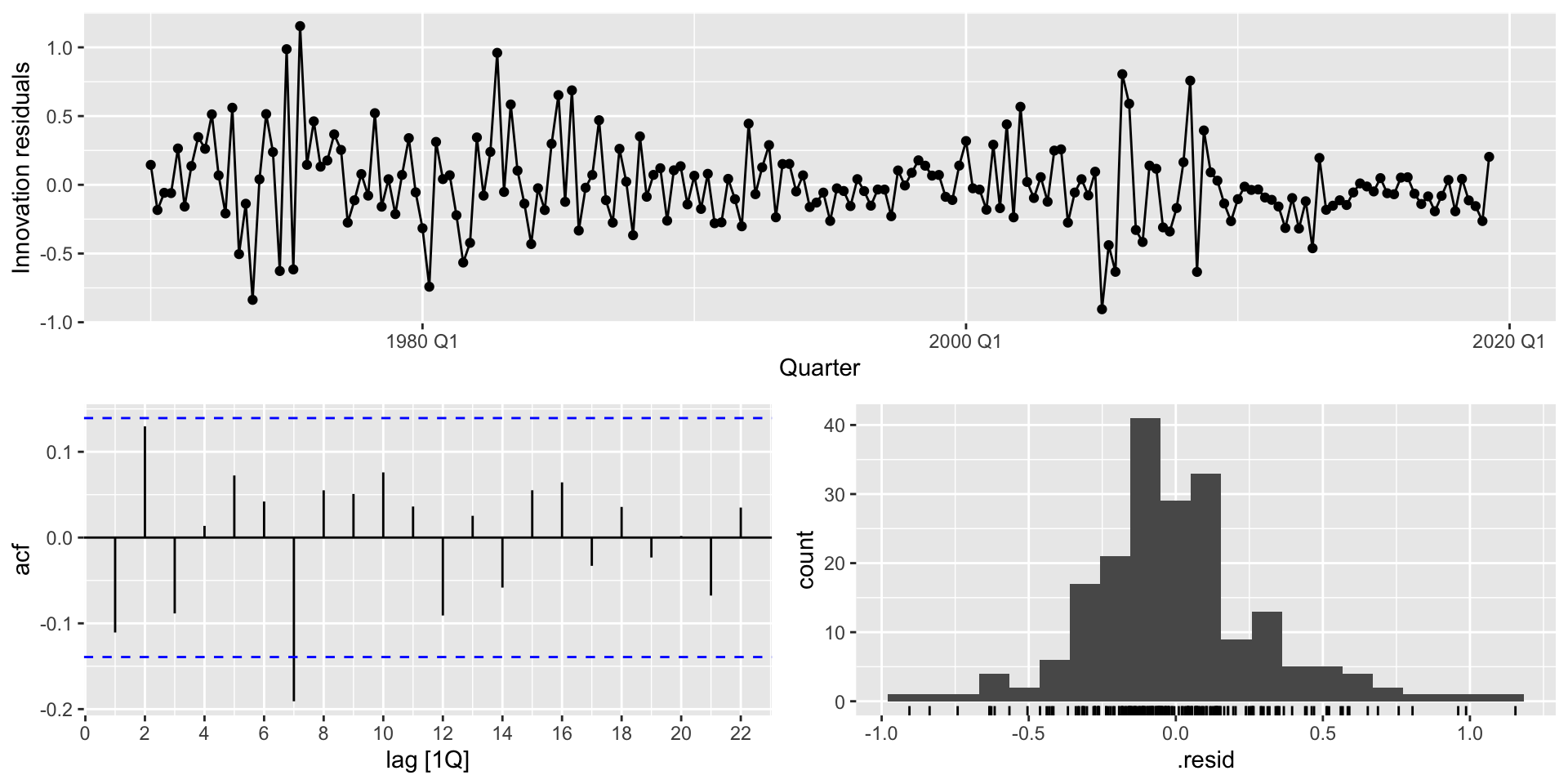
1 TSLM(Consumption ~ Income + Production + Savings + Unemploy… 17.1 0.000671Por quê 8 e 5?
Regressões espúrias
Regressões espúrias
Quando trabalhamos com séries temporais, na maioria das vezes, as séries são não estacionárias, ou seja os valores da série não flutuam ao redor de uma média constante e/ou variância constante.
Processo estacionário
Um proceso estocástico \(\{Y_t\}_{t = -\infty}^{\infty}\) é dito (fracamente) estacionário se:
- \(\mathbb{E}(Y_t^2) < \infty, \quad \forall t\)
- \(\mathbb{E}(Y_t) = \mu_t = \mu, \quad \forall t\)
- \(\mathbb{Cov}(Y_t, Y_{t+h})\) depende somente de \(h\) e não de \(t\).
Na maioria das vezes, ao ajustar um modelo de regressão em séries não estacionárias encontraremos um \(R^2\) alto e \(\beta\)s significativos (parecendo termos encontrado um “bom” modelo). Contudo, esta descoberta é espúria (falsa).
Regressões espúrias
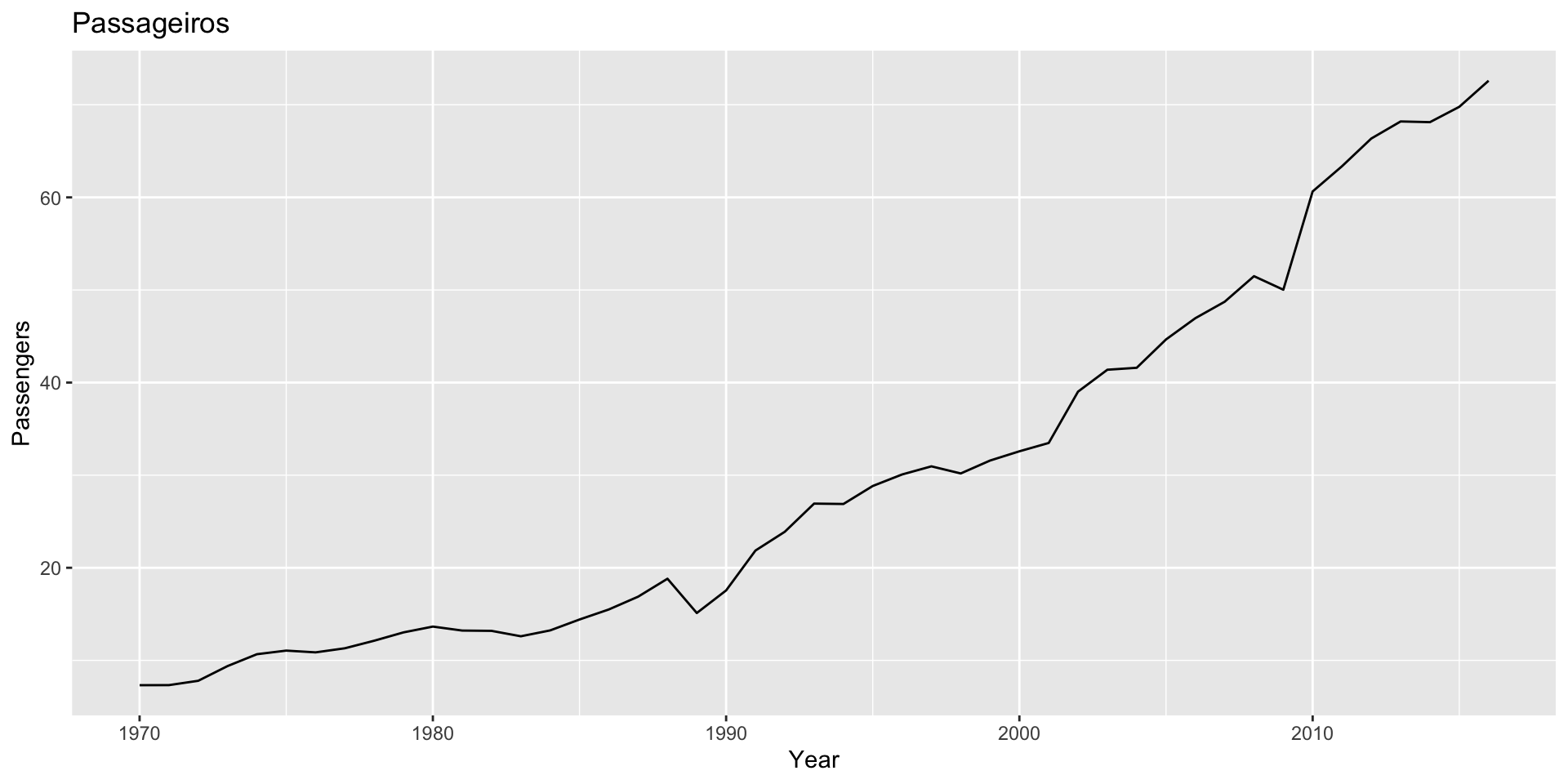
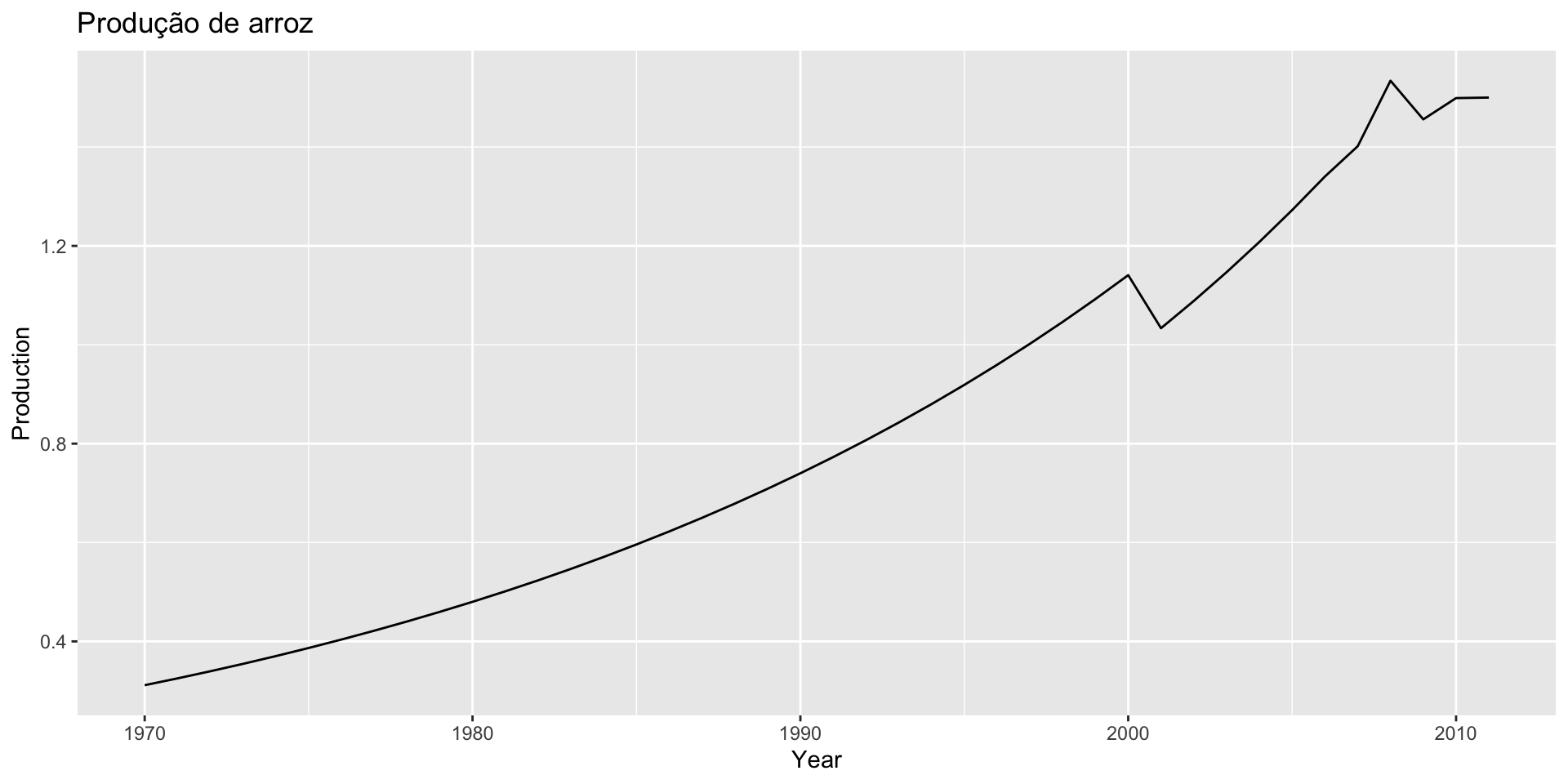
Os datasets aus_airpassengers a guinea_rice do pacote fpp3, contém informações do número total de passageiros (em milhões) na Austrália e da produção anual de arroz (em milhões de toneladas) na Guiné, respectivamente.
As séries não tem nenhuma relação, a não ser que ambas são não estacionárias.
Regressões espúrias
\[Passageiros= \beta_0 + \beta_1 \text{Produção de Arroz} + e\]
Code
Series: Passengers
Model: TSLM
Residuals:
Min 1Q Median 3Q Max
-5.9448 -1.8917 -0.3272 1.8620 10.4210
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -7.493 1.203 -6.229 2.25e-07 ***
Production 40.288 1.337 30.135 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 3.239 on 40 degrees of freedom
Multiple R-squared: 0.9578, Adjusted R-squared: 0.9568
F-statistic: 908.1 on 1 and 40 DF, p-value: < 2.22e-16Aparentemente, temos um achado!! a cada unidade de aumento na produção de arroz na Guiné, o número de passageiros na Austrália aumenta em 40 unidades 🤣
Regressões espúrias
A falsa descoberta (espúria) encontrada anteriormente é devido à não estacionariedade das séries. Informalmente falando, essa não estacionariedade faz com que encontremos relações onde não há (elas são confundidas pelas tendências de ambas as séries).
Cuidado! Muitos dos grandes achados encontrados por aí são, na verdade, relações espúrias. Analise tudo!
Fiz uma regressão em um contexo de séries temporais, como sei se ela é espúria?
- Utilizou séries não estacionárias?
- Obteve um \(R^2\) bem alto?
- Os resíduos são autocorrelacionádos?
Se a resposta for SIM, regressão espúria detetada!
Regressões espúrias
Mas, como sei se a série que estou utilizando é não estacionária?
- Lembre-se da definição da estacionariedade!.
- Graficamente, se a série tiver tendência e/ou a variabilidade aumentar (ou diminuir) ao longo do tempo, a série é não estacionária.
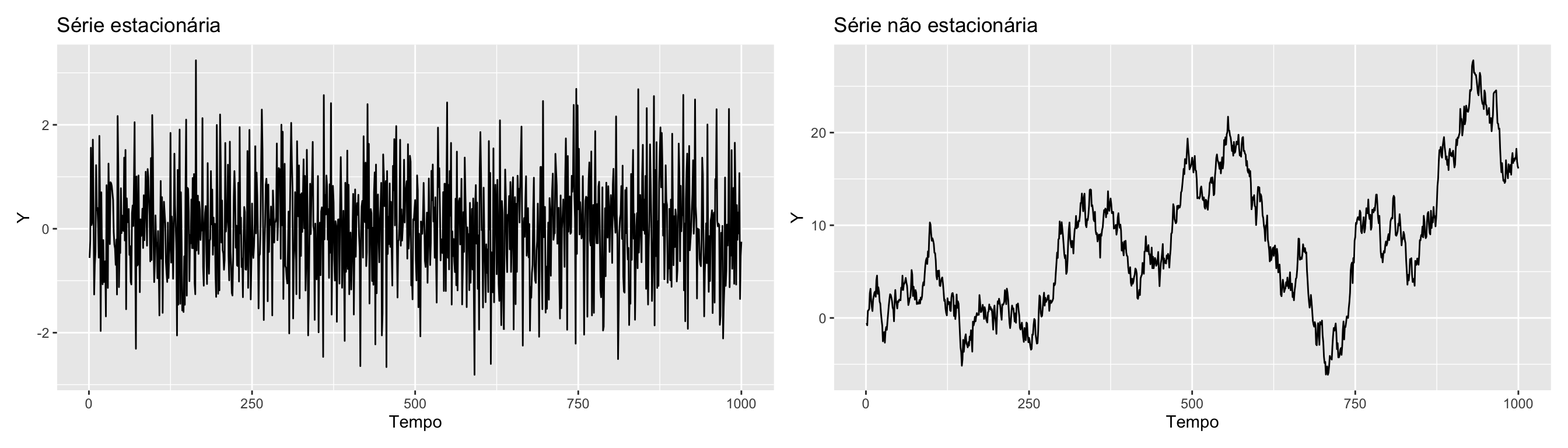
Regressões espúrias
Às vezes, olhando para o gráfico da série temporal, não é facil de verificar se a série é não estacionária.
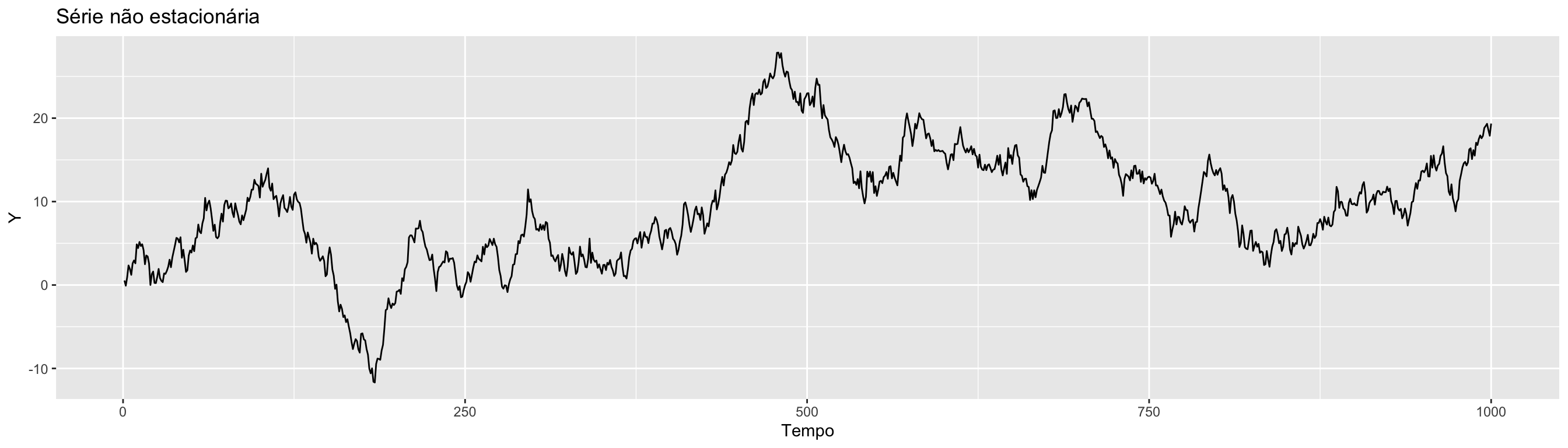
Gráfico alternativo: função de autocorrelação (correlograma): Se as autocorrelações forem significativas e cairem devagar 🐢 , a série é não estacionária.
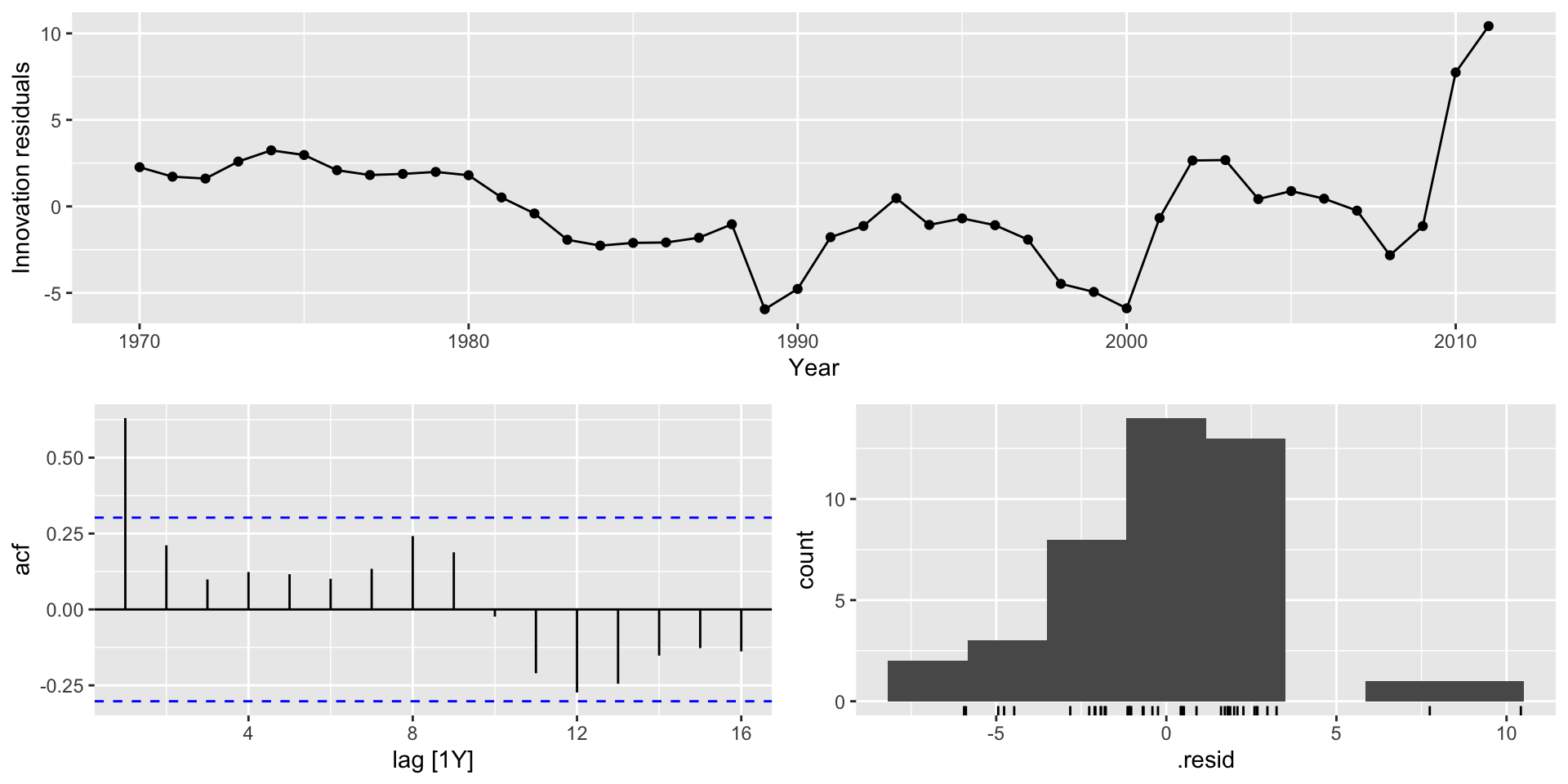
Regressões espúrias
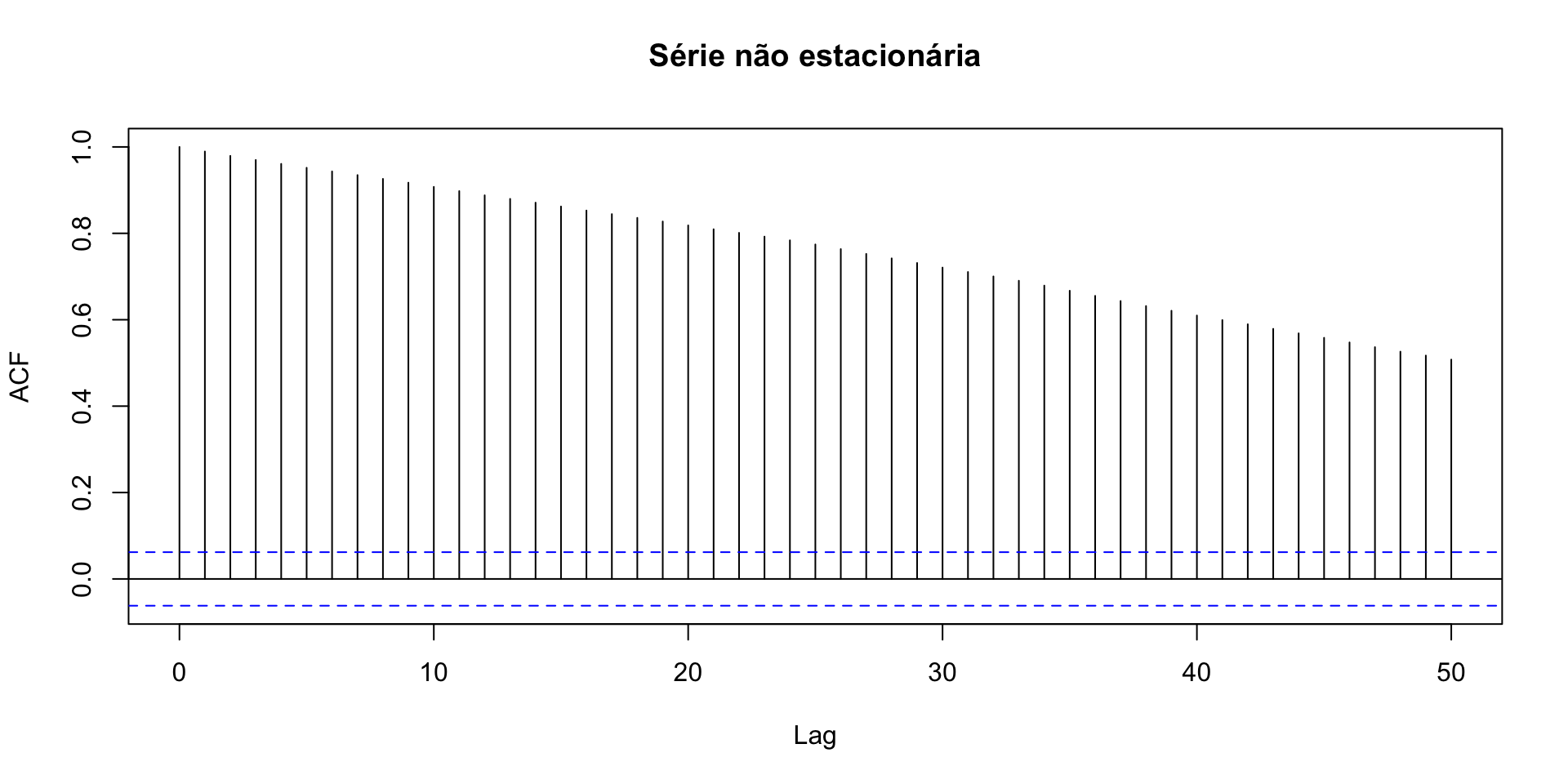
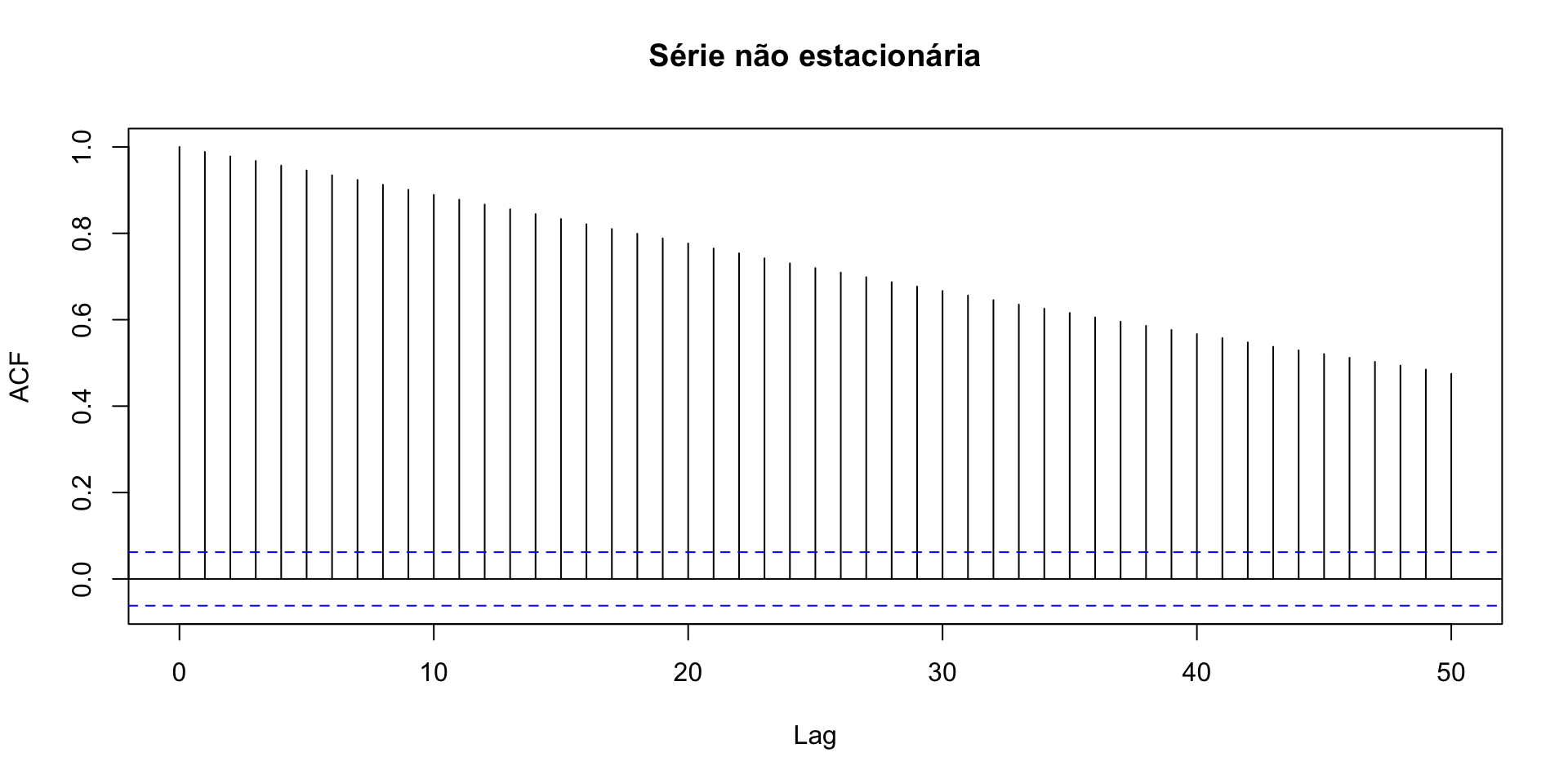
Se as autocorrelações forem significativas e cairem devagar, a série é não estacionária.
Regressões espúrias

Em alguns casos, existem alternativas simples para continuar utilizando modelos de regressão no contexto de séries temporais e não cair na regressão espúria.
Séries com tendência e modelos de regressão
Séries com tendência e modelos de regressão
Lembrando
A decomposição de séries temporais pode ser definida como
\[\underbrace{Y_t = T_t + S_t + R_t}_{\text{Modelo aditivo}} \quad ou \quad \underbrace{Y_t = T_t \times S_t \times R_t}_{\text{Modelo multiplicativo}}\]
Fazendo algumas modificações, podemos transformar a equação acima em um modelo de regressão da forma
\[Y_t = \beta_0 + \beta_1 T_t + \beta_2 S_t + \epsilon_t\]
\[\text{ou} \quad \log(Y_t) = \beta_0 + \beta_1 \log(T_t) + \beta_2 \log(S_t) + \epsilon_t\]
Bastando apenas saber quem utilizarmos como \(T_t\) e quem como \(S_t\).
Séries com tendência e modelos de regressão
Alternativa 1:
Quando as séries têm alguma tendência (linear, quadrática, cúbica, exponencial, etc), podemos incluir algumas variaveis explicativas no modelo que nos ajudarão a capturar o comportamento da tendência e fugir das regressões espúrias.
- Tendência Linear: \(y_t = \alpha_0 + \alpha_1t + e_t\)
- Tendência Quadrática: \(y_t = \alpha_0 + \alpha_1t + \alpha_2 t^2 +e_t\)
- Tendência Cúbica: \(y_t = \alpha_0 + \alpha_1t + \alpha_2 t^2 + \alpha_3 t^3+e_t\)
- Tendência Exponencial: \(\log(y_t) = \alpha_0 + \alpha_1t + e_t\) ( \(y_t > 0\))
Incluir \(t\), \(t^2\), \(t^3\), … no modelo, atuará como um removedor de tendência
Séries com tendência e modelos de regressão
- Incluiremos uma tendência quadrática no modelo.
- Para isso, utilizaremos a função
trend()que funciona como um \(t\) na equação de regressão.
Code
Series: Passengers
Model: TSLM
Residuals:
Min 1Q Median 3Q Max
-4.17183 -1.25445 -0.01282 1.23435 4.08528
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 10.46423 2.94060 3.559 0.00102 **
Production -2.72724 9.45961 -0.288 0.77468
trend() -0.14602 0.16021 -0.911 0.36783
I(trend()^2) 0.03347 0.00452 7.405 7.01e-09 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2.001 on 38 degrees of freedom
Multiple R-squared: 0.9847, Adjusted R-squared: 0.9835
F-statistic: 815.6 on 3 and 38 DF, p-value: < 2.22e-16Séries com tendência e modelos de regressão
- Ao remover o efeito da tendência,
Productionnão é mais estatísticamente significativa, o que faz muito mais sentido 🏄♀️ 🏄♀️. - Mesmo com a variável
Productionnão sendo estatísticamente significativa, o \(R^2\) do modelo deu \(\approx\) 0.98!. Será que o modelo capturou mesmo a dinâmica dos dados?
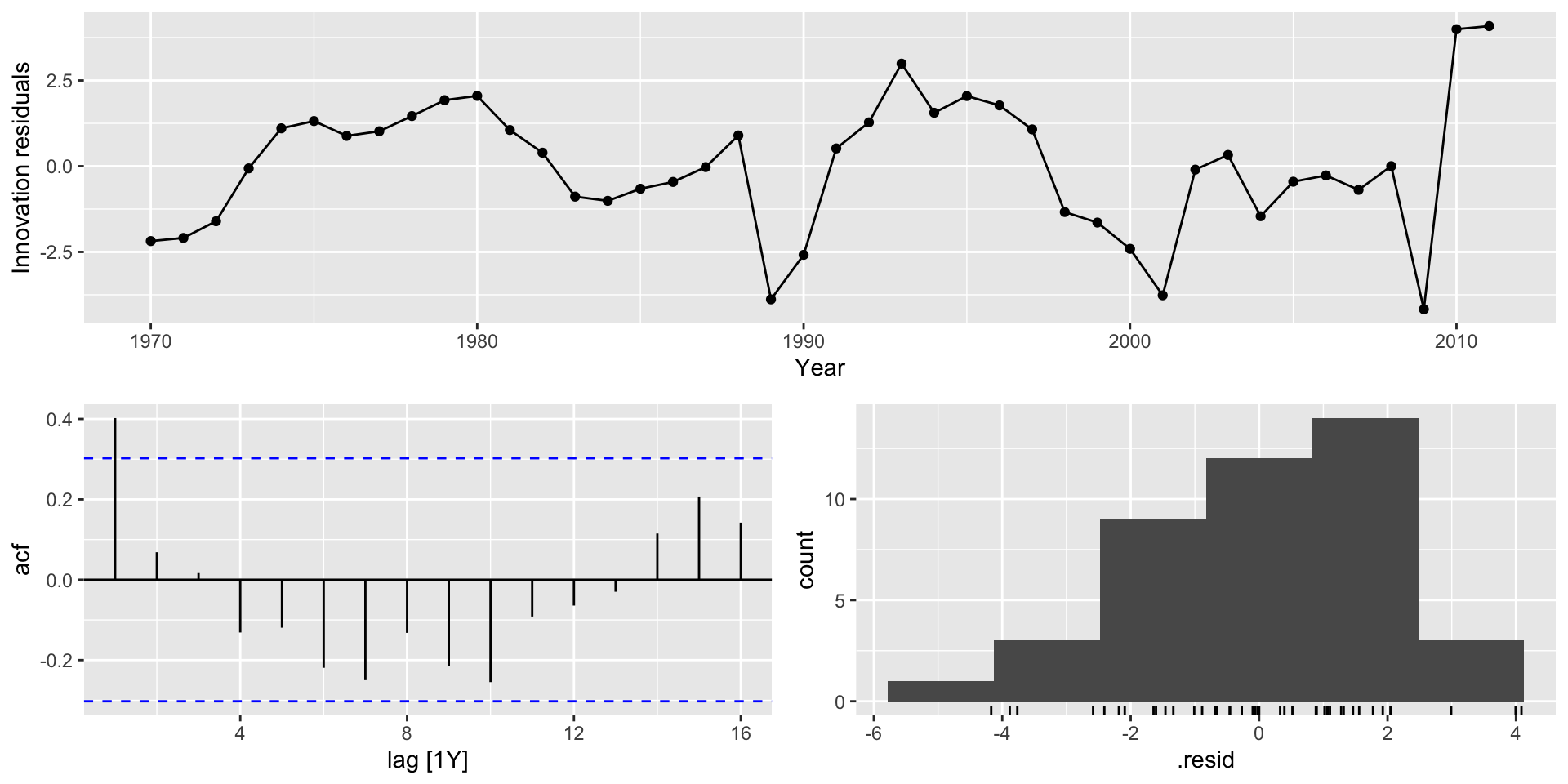
Séries com tendência e modelos de regressão
Cuidado, quando trabalharmos com séries temporais não estacionárias, não devemos olhar para o \(R^2\).
Se quisermos utilizar o \(R^2\) precisamos fazer alguns ajustes. Ver o artigo do Wooldridge (1991) para mais detalhes
Como saber se incluir uma tendência temporal no modelo?
- Se alguma variavel (dependênte ou independênte) apresentar tendência, então incluir t (ou \(t^2\) ou \(t^3\)) é uma boa ideia.
- Se ao incluir a tendência temporal, o termo de tendência for estatísticamente significativo e os resultados mudarem de forma susbtancial, o modelo deve incluir a tendência temporal mesmo.
- Se o tendência temporal não for incluida, então nao ocorrera remoção da tendência e poderemos encontrar relaciones espúrias (grandes achados que na verdade são espúrios).
Referências
- Hyndman, R.J., & Athanasopoulos, G. (2021). Forecasting: principles and practice, 3rd edition, OTexts: Melbourne, Australia. OTexts.com/fpp3.. Chapter 7.
- Krispin, R. (2019). Hands-On Time Series Analysis with R: Perform time series analysis and forecasting using R. Packt Publishing Ltd. Chapter 9
- Wooldridge, Jeffrey M. (2016). Introdução à Econometria: Uma abordagem moderna. Cengage Learning. – Cap 10
- Wooldridge, J. M. (1991). A note on computing r-squared and adjusted r-squared for trending and seasonal data. Economics Letters, 36(1), 49-54.
- Trucíos, C. (2021, Feb. 28). Carlos Trucíos: Teorema de Gauss-Markov. Retrieved from https://ctruciosm.github.io/posts/2021-02-28-teorema-de-gauss-markov/ .

Carlos Trucíos (IMECC/UNICAMP) | ME607 - Séries Temporais | ctruciosm.github.io