Decomposição de séries temporais

ME607 - Séries Temporais

Prof. Carlos Trucíos
ctrucios@unicamp.br

Instituto de Matemática, Estatística e Computação Científica (IMECC),
Universidade Estadual de Campinas (UNICAMP).

Agenda

• Introdução
• Transformações
• Decomposição
• Decomposição clássica
• Outros métodos de decomposição

Introdução

Introdução

• Aprenderemos métodos para extrair essas componentes da séries observada. Isto é feito com fins descritivos (entender a série) mas também para melhorar a acurácia das previsões.

• Tendência: Componente a longo prazo e indica um aumento/diminuição.

• Sazonalidade: Oscilações que se produzem e repetem em curtos períodos de tempo (semanal, mensal, trimestral,…)

• Aleatoriedade: A parte que não é explicada pelas componentes anteriores.

Transformações

Transformações e ajustes

• Quando formos decompor a série, é conveniente primeiro transformar/ajustar a série antes de fazer a decomposição.
• Estes tipo de transformações podem ser to tipo (a) ajustes calendârio, (b) ajustes populacionais, (c) ajustes pela inflação e (d) transformações matemáticas.
• O objetivo destas transformações é remover fontes conhecidas de variação e/ou fazer os padrões mais consistentes ao longo da série toda.

Transformações e ajustes

Ajustes calendário

Quando trabalhamos com dados sazonais, primeiro removemos o efeito calendário. Ex: quando trabalhamos com dados mensais é importante levar em consideração o número de dias úteis (ou dias calendário) dentro de cada mês. Isto pode ser feito utilizando a média diária em lugar do total mensal.

Ajustes populacionais

Qualquer série temporal que esteja afetada população pode ser transformada em séries per capita (ou por milhões de habitantes).

Ajustes de inflação

Dados que são afetados pelo valor do dinheiro devem ser ajustados pela inflação antes de serem analisados.

Transformações e ajustes

Transformações matemáticas

• Se os dados apresentam variações que aumentam ou diminuem com o nível da série, transformações matemáticas podem ser utilizadas.
• Transformação logaritmica: \(\log(\cdot)\) são interessantes pois são interpretáveis. Mudanças nos valores em log são mudanças (em porcentagem) na escala original.
• Transformação potência: \(y_t^p\), valores de \(p\) usuais são 1/2 ou 1/3.
• Transformação Box-Cox: \[\begin{equation} w_t= \begin{cases} \dfrac{sign(y_t)|y_t|^{\lambda}-1}{\lambda} & \text{se } \lambda \neq 0, \\ \log(y_t) & \text{se } \lambda = 0. \end{cases} \end{equation}\]
• Um “bom” valor de \(\lambda\) é aquele que faz com que o tamanho da variação sazonal seja a mesma ao longo de toda a série.

Decomposição

Decomposição

Após o gráfico de sequência, talvez identifiquemos que a série pode ser escrita como:

\[\underbrace{y_t = T_t + S_t + R_t}_{Decomposição \quad aditiva} \quad ou \quad \underbrace{y_t = T_t \times S_t \times R_t}_{Decomposição \quad multiplicativa}\]

• \(T_t:\) componente de tendência (ou tendência-ciclo).
• \(S_t:\) componente sazonal.
• \(R_t:\) componente aleatoria.

Se a magnitude das variações sazonais não varia com o nível, então utilizamos uma decomposição aditiva. Caso contrário, uma decomposição multiplicativa.

Decomposição

Aditivo ou Multiplicativo

Se a magnitude das variações sazonais não varia com o nível, então utilizamos uma decomposição aditiva. Caso contrário, uma decomposição multiplicativa.

Obs: \[y_t = T_t \times S_t \times R_t \quad \rightarrow \quad \log(y_t) = \log(T_t) + \log(S_t) + \log(R_t)\]

Decomposição

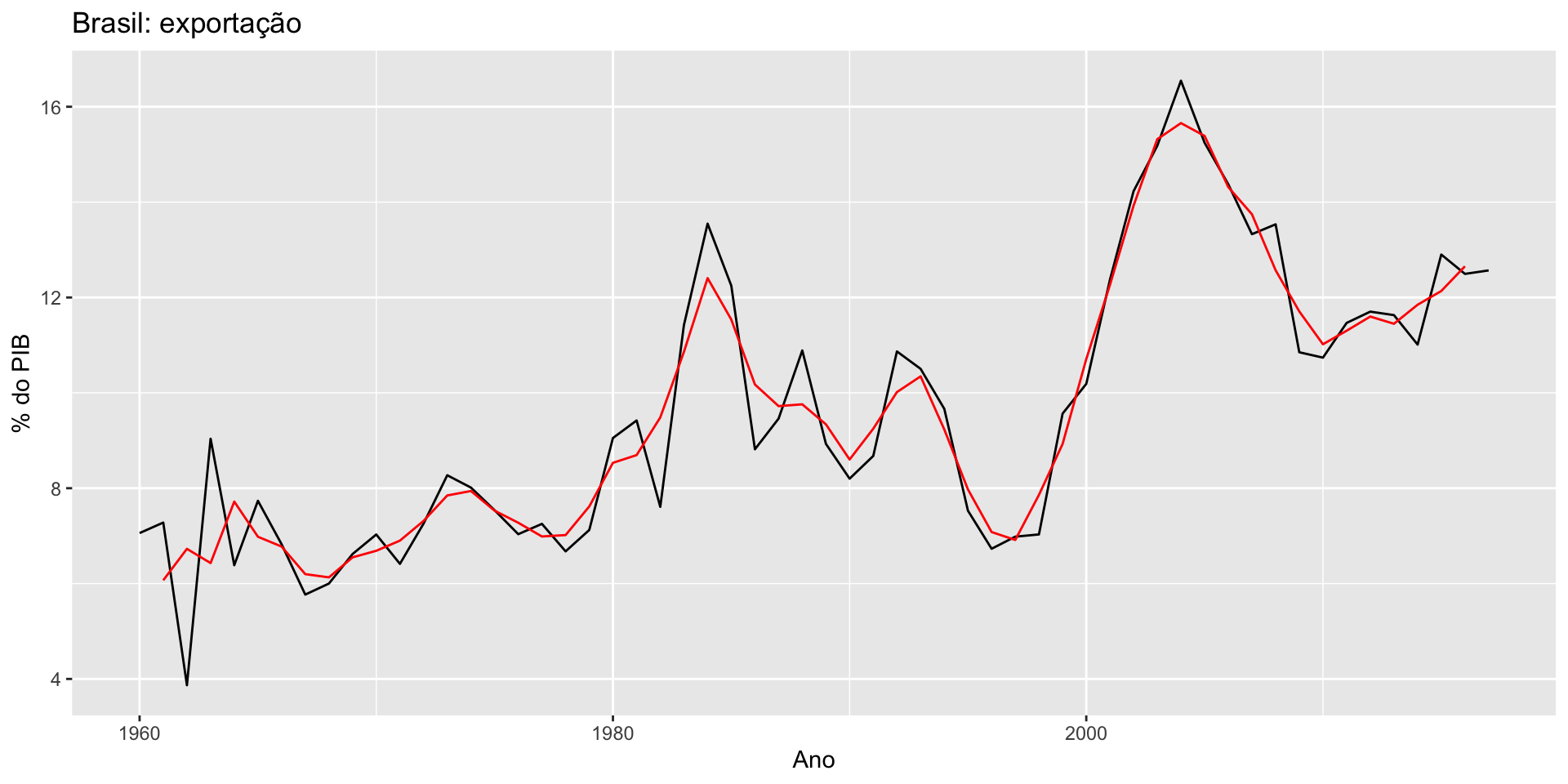
Suponha que temos a seguinte série temporal

Decomposição

O objetivo é decompor a série na suas componentes.

Decomposição

Série sazonalmente ajustada

Se a componente sazonal é removida da série, dizemos que a serié é sazonalmente ajustada. Esta série sazonalmente ajustada é dada (dependendo se utilizarmos uma decomposição aditiva ou multiplicativa) por \[y_t - S_t \quad ou \quad y_t/S_t\]

Decomposição clássica

Decomposição clássica

Antes de entrarmos em detalhes a respeito de como é feita a decomposição, veremos alguns métodos clássicos para estimar \(T_t\).

Médias Móveis (1920s)

É um dos métodos mais clássicos para estimar \(T_t\). Estimamos \(T_t\) por

\[\hat{T}_t = \dfrac{1}{m}\displaystyle \sum_{i=-k}^k y_{t+i},\]em que \(m = 2k+1\) e a média movel é dita de ordem \(m\) (ou \(m\)-MM)

• A MM suaviza a série original e captura os principais movimentos da série
• O valor de \(m\) determina quão suavizada será a série.

Decomposição clássica

• 5-MM
• 9-MM
• 15-MM

Code

global_economy |> 
  filter(Country == "Brazil") |> 
  mutate(`5-MM` = slider::slide_dbl(Exports, mean, .before = 2, .after = 2, .complete = TRUE)) |> 
  autoplot(Exports) + geom_line(aes(y = `5-MM`), colour = "red") +
  labs(y = "% do PIB", title = "Brasil: exportação", x = "Ano")

Code

global_economy |> 
  filter(Country == "Brazil") |> 
  mutate(`9-MM` = slider::slide_dbl(Exports, mean, .before = 4, .after = 4, .complete = TRUE)) |> 
  autoplot(Exports) + geom_line(aes(y = `9-MM`), colour = "red") +
  labs(y = "% do PIB", title = "Brasil: exportação", x = "Ano")

Code

global_economy |> 
  filter(Country == "Brazil") |> 
  mutate(`15-MM` = slider::slide_dbl(Exports, mean, .before = 7, .after = 7, .complete = TRUE)) |> 
  autoplot(Exports) + geom_line(aes(y = `15-MM`), colour = "red") +
  labs(y = "% do PIB", title = "Brasil: exportação", x = "Ano")

Decomposição clássica

• A definição de MM utilizada permite que, para \(m\) ímpar, existe uma simetria.
• O que fazer se quisermos manter a simetria mas utilizar \(m\) par?

Médias Móveis das Médias Móveis

Code

beer <- aus_production |> 
  filter(year(Quarter) >= 1992) |> 
  select(Quarter, Beer)
beer_ma <- beer |> 
  mutate( `4-MM` = slider::slide_dbl(Beer, mean,.before = 1, .after = 2, .complete = TRUE),
          `2x4-MM` = slider::slide_dbl(`4-MM`, mean,  .before = 1, .after = 0, .complete = TRUE))
beer_ma

# A tsibble: 74 x 4 [1Q]
   Quarter  Beer `4-MM` `2x4-MM`
     <qtr> <dbl>  <dbl>    <dbl>
 1 1992 Q1   443    NA       NA 
 2 1992 Q2   410   451.      NA 
 3 1992 Q3   420   449.     450 
 4 1992 Q4   532   452.     450.
 5 1993 Q1   433   449      450.
 6 1993 Q2   421   444      446.
 7 1993 Q3   410   448      446 
 8 1993 Q4   512   438      443 
 9 1994 Q1   449   441.     440.
10 1994 Q2   381   446      444.
# … with 64 more rows

Mas o que estamos fazendo de fato?

Decomposição clássica

Um conceito ainda mais geral que envolve ambos os casos desscritos anteriormente é o de médias móveis ponderadas.

Médias Móveis Ponderadas

\[\hat{T}_t = \displaystyle \sum_{j = -k}^k a_k y_{t+j},\] em que \(\displaystyle \sum_{j = -k}^k a_k = 1\) e \(a_j = a_{-j}\).

• Note que para \(m = 2k + 1\) e \(a_{-k} = \cdots = a_{k} = \dfrac{1}{m}\), temos \(m\)-MM.
• \(2 \times m - MM\) é obtido fazendo \(a_{-k+1} = \cdots = a_{k-1} = 1/m\) e \(a_{-k} = a_k = 1/2m\) (\(a_i = 1/m\) exceto nos extremos, em que \(a_i = 1/2m\)).

Decomposição clássica

Modelo Aditivo

\[y_t = T_t + S_t + R_t\]

• Passo 1: Estimar \(T_t\) através e um \(m\)-MM ou \(2-m-MM\).
• Passo 2: Remover tendência: \(y_t - \hat{T}_t\).
• Passo 3: Estimar \(S_t\) através da média das \(y_t - \hat{T}_t\) para esse ponto sazonal. (Ex: se trabalharmos com dados mensais, calcular a média de todas as observações em Janeiro, depois Fevereiro, ….).
• Passo 4: Calcular \(\hat{R}_t = y_t - \hat{T}_t - \hat{S}_t\).

Modelo Multiplicativo

\[y_t = T_t \times S_t \times R_t\]

• Passo 1: Estimar \(T_t\) através e um \(m\)-MM ou \(2-m-MM\).
• Passo 2: Remover tendência: \(y_t/\hat{T}_t\).
• Passo 3: Estimar \(S_t\) através da média das \(y_t/\hat{T}_t\) para esse ponto sazonal. (Ex: se trabalharmos com dados mensais, calcular a média de todas as observações em Janeiro, depois Fevereiro, ….).
• Passo 4: Calcular \(\hat{R}_t = y_t/(\hat{T}_t \times \hat{S}_t)\).

Decomposição clássica

• Importar dados
• Gráfico
• Decomposição
• Decomposição Gráfico
• Obs

Code

library(tsibble)     
library(dplyr) 
url <- "https://raw.githubusercontent.com/jbrownlee/Datasets/master/airline-passengers.csv"
passageiros <- read.csv(url) 
glimpse(passageiros) # R ainda não sabe que nossos dados são de séries temporais

Rows: 144
Columns: 2
$ Month      <chr> "1949-01", "1949-02", "1949-03", "1949-04", "1949-05", "194…
$ Passengers <int> 112, 118, 132, 129, 121, 135, 148, 148, 136, 119, 104, 118,…

Code

passageiros <- passageiros %>% mutate(Month = yearmonth(Month)) %>% as_tsibble(index = Month)
glimpse(passageiros) # Agora R sabe sim!

Rows: 144
Columns: 2
$ Month      <mth> 1949 Jan, 1949 Feb, 1949 Mar, 1949 Apr, 1949 May, 1949 Jun,…
$ Passengers <int> 112, 118, 132, 129, 121, 135, 148, 148, 136, 119, 104, 118,…

Code

ggplot(passageiros) + geom_line(aes(x = Month, y = Passengers))

Code

dcmp <- passageiros %>%   # passageiros é do tipo tsibble
  model(decomposition = classical_decomposition(Passengers,
                                                type = "mult")) %>% 
  components() 
dcmp

# A dable: 144 x 7 [1M]
# Key:     .model [1]
# :        Passengers = trend * seasonal * random
   .model           Month Passengers trend seasonal random season_adjust
   <chr>            <mth>      <int> <dbl>    <dbl>  <dbl>         <dbl>
 1 decomposition 1949 Jan        112   NA     0.910 NA              123.
 2 decomposition 1949 Feb        118   NA     0.884 NA              134.
 3 decomposition 1949 Mar        132   NA     1.01  NA              131.
 4 decomposition 1949 Apr        129   NA     0.976 NA              132.
 5 decomposition 1949 May        121   NA     0.981 NA              123.
 6 decomposition 1949 Jun        135   NA     1.11  NA              121.
 7 decomposition 1949 Jul        148  127.    1.23   0.952          121.
 8 decomposition 1949 Aug        148  127.    1.22   0.953          121.
 9 decomposition 1949 Sep        136  128.    1.06   1.00           128.
10 decomposition 1949 Oct        119  129.    0.922  1.00           129.
# … with 134 more rows

Code

passageiros %>%   # passageiros é do tipo tsibble
  model(classical_decomposition(Passengers, type = "multiplicative")) %>% 
  components() %>%  # extraimos as componentes T_t, S_t e R_t
  autoplot()

• Além da função yearmonth() do pacote tsibble, outras funções úteis são yearquarter(), yearweek(), as_date(), ymd(), ymd_hms().
• O argumento type dentro de classical_decomposition() pode ser “multiplicative” ou “aditive”, dependendo do tipo de decomposição a ser utilizada.

Decomposição clássica

• Utils 1
• Tt
• St
• St*
• Obs.

Code

media_movel_par <- function(x, m) {
  k <- m/2
  n <- length(x)
  Tt <- rep(NA, n)
  pesos <- rep(1/m, m + 1)
  pesos[1] <- 1/(2*m)
  pesos[m + 1] <- 1/(2*m)
  for (i in (k + 1):(n - k)) {
    Tt[i] <- sum(pesos * x[(i - k):(i + k)])
  }
  return(Tt)
}

Code

library(stringi)
library(stringr)
url <- "https://raw.githubusercontent.com/jbrownlee/Datasets/master/airline-passengers.csv"
passageiros_hand <- read.csv(url) 
passageiros_hand <- passageiros_hand |> 
  mutate(Tt = media_movel_par(Passengers, 12)) |> 
  mutate(At = Passengers/Tt)  # Removemos a tendência
cbind(passageiros_hand$Tt, dcmp$trend)

           [,1]     [,2]
  [1,]       NA       NA
  [2,]       NA       NA
  [3,]       NA       NA
  [4,]       NA       NA
  [5,]       NA       NA
  [6,]       NA       NA
  [7,] 126.7917 126.7917
  [8,] 127.2500 127.2500
  [9,] 127.9583 127.9583
 [10,] 128.5833 128.5833
 [11,] 129.0000 129.0000
 [12,] 129.7500 129.7500
 [13,] 131.2500 131.2500
 [14,] 133.0833 133.0833
 [15,] 134.9167 134.9167
 [16,] 136.4167 136.4167
 [17,] 137.4167 137.4167
 [18,] 138.7500 138.7500
 [19,] 140.9167 140.9167
 [20,] 143.1667 143.1667
 [21,] 145.7083 145.7083
 [22,] 148.4167 148.4167
 [23,] 151.5417 151.5417
 [24,] 154.7083 154.7083
 [25,] 157.1250 157.1250
 [26,] 159.5417 159.5417
 [27,] 161.8333 161.8333
 [28,] 164.1250 164.1250
 [29,] 166.6667 166.6667
 [30,] 169.0833 169.0833
 [31,] 171.2500 171.2500
 [32,] 173.5833 173.5833
 [33,] 175.4583 175.4583
 [34,] 176.8333 176.8333
 [35,] 178.0417 178.0417
 [36,] 180.1667 180.1667
 [37,] 183.1250 183.1250
 [38,] 186.2083 186.2083
 [39,] 189.0417 189.0417
 [40,] 191.2917 191.2917
 [41,] 193.5833 193.5833
 [42,] 195.8333 195.8333
 [43,] 198.0417 198.0417
 [44,] 199.7500 199.7500
 [45,] 202.2083 202.2083
 [46,] 206.2500 206.2500
 [47,] 210.4167 210.4167
 [48,] 213.3750 213.3750
 [49,] 215.8333 215.8333
 [50,] 218.5000 218.5000
 [51,] 220.9167 220.9167
 [52,] 222.9167 222.9167
 [53,] 224.0833 224.0833
 [54,] 224.7083 224.7083
 [55,] 225.3333 225.3333
 [56,] 225.3333 225.3333
 [57,] 224.9583 224.9583
 [58,] 224.5833 224.5833
 [59,] 224.4583 224.4583
 [60,] 225.5417 225.5417
 [61,] 228.0000 228.0000
 [62,] 230.4583 230.4583
 [63,] 232.2500 232.2500
 [64,] 233.9167 233.9167
 [65,] 235.6250 235.6250
 [66,] 237.7500 237.7500
 [67,] 240.5000 240.5000
 [68,] 243.9583 243.9583
 [69,] 247.1667 247.1667
 [70,] 250.2500 250.2500
 [71,] 253.5000 253.5000
 [72,] 257.1250 257.1250
 [73,] 261.8333 261.8333
 [74,] 266.6667 266.6667
 [75,] 271.1250 271.1250
 [76,] 275.2083 275.2083
 [77,] 278.5000 278.5000
 [78,] 281.9583 281.9583
 [79,] 285.7500 285.7500
 [80,] 289.3333 289.3333
 [81,] 293.2500 293.2500
 [82,] 297.1667 297.1667
 [83,] 301.0000 301.0000
 [84,] 305.4583 305.4583
 [85,] 309.9583 309.9583
 [86,] 314.4167 314.4167
 [87,] 318.6250 318.6250
 [88,] 321.7500 321.7500
 [89,] 324.5000 324.5000
 [90,] 327.0833 327.0833
 [91,] 329.5417 329.5417
 [92,] 331.8333 331.8333
 [93,] 334.4583 334.4583
 [94,] 337.5417 337.5417
 [95,] 340.5417 340.5417
 [96,] 344.0833 344.0833
 [97,] 348.2500 348.2500
 [98,] 353.0000 353.0000
 [99,] 357.6250 357.6250
[100,] 361.3750 361.3750
[101,] 364.5000 364.5000
[102,] 367.1667 367.1667
[103,] 369.4583 369.4583
[104,] 371.2083 371.2083
[105,] 372.1667 372.1667
[106,] 372.4167 372.4167
[107,] 372.7500 372.7500
[108,] 373.6250 373.6250
[109,] 375.2500 375.2500
[110,] 377.9167 377.9167
[111,] 379.5000 379.5000
[112,] 380.0000 380.0000
[113,] 380.7083 380.7083
[114,] 380.9583 380.9583
[115,] 381.8333 381.8333
[116,] 383.6667 383.6667
[117,] 386.5000 386.5000
[118,] 390.3333 390.3333
[119,] 394.7083 394.7083
[120,] 398.6250 398.6250
[121,] 402.5417 402.5417
[122,] 407.1667 407.1667
[123,] 411.8750 411.8750
[124,] 416.3333 416.3333
[125,] 420.5000 420.5000
[126,] 425.5000 425.5000
[127,] 430.7083 430.7083
[128,] 435.1250 435.1250
[129,] 437.7083 437.7083
[130,] 440.9583 440.9583
[131,] 445.8333 445.8333
[132,] 450.6250 450.6250
[133,] 456.3333 456.3333
[134,] 461.3750 461.3750
[135,] 465.2083 465.2083
[136,] 469.3333 469.3333
[137,] 472.7500 472.7500
[138,] 475.0417 475.0417
[139,]       NA       NA
[140,]       NA       NA
[141,]       NA       NA
[142,]       NA       NA
[143,]       NA       NA
[144,]       NA       NA

Code

# Calculamos a componente Sazonal
passageiros_st = passageiros_hand |> 
  mutate(Month = month(yearmonth(Month))) |> 
  group_by(Month) |> 
  summarise(St = mean(At, na.rm = TRUE)) |> 
  ungroup()
cbind(passageiros_st$St, dcmp$seasonal[1:12])

           [,1]      [,2]
 [1,] 0.9086244 0.9102304
 [2,] 0.8820663 0.8836253
 [3,] 1.0055889 1.0073663
 [4,] 0.9741842 0.9759060
 [5,] 0.9796465 0.9813780
 [6,] 1.1108125 1.1127758
 [7,] 1.2243915 1.2265555
 [8,] 1.2177586 1.2199110
 [9,] 1.0586209 1.0604919
[10,] 0.9201309 0.9217572
[11,] 0.7997645 0.8011781
[12,] 0.8972386 0.8988244

Code

# Calculamos a componente Sazonal
mu = mean(passageiros_st$St)
mu

[1] 0.9982357

Code

passageiros_st$St/mu

 [1] 0.9102304 0.8836253 1.0073663 0.9759060 0.9813780 1.1127758 1.2265555
 [8] 1.2199110 1.0604919 0.9217572 0.8011781 0.8988244

Code

dcmp$seasonal[1:12]

 [1] 0.9102304 0.8836253 1.0073663 0.9759060 0.9813780 1.1127758 1.2265555
 [8] 1.2199110 1.0604919 0.9217572 0.8011781 0.8988244

• Estimamos \(S_t\) através da média das \(y_t - \hat{T}_t\) (ou \(y_t/\hat{T}_t\) se a decomposição for multiplicativa).
• Na decomposição aditiva, é comum preferir estimar \(S_t\) por \[\hat{S_t}^{\ast} = \hat{S}_t - \dfrac{1}{m} \displaystyle \sum_{i = 1}^m \hat{S}_i\]
• Na decomposição multiplicativa, é comum preferir estimar \(S_t\) por \[\hat{S_t}^{\ast} = \hat{S}_t / \dfrac{1}{m} \displaystyle \sum_{i = 1}^m \hat{S}_i\]

Outros métodos de decomposição

Outros métodos de decomposição

O método clássico de decomposição possui algumas limitações que fazem dele um método pouco recomendado nos dias de hoje:

• Como utilizamos médias móveis, a componente de tendência não possui valores nas primeiras nem últimas observações.
• A componente sazonal \(S_t\) é obtida assumindo que é constante.
• Não é possível obter valores de \(\hat{R}_t\) para as primeiras ou últimas observações.
• Não é robusto a observações atípicas.

Outros métodos de decomposição como X-11, SEATS (Seasonal Extraction in ARIMA Time Series) e STL (Seasonal and Trend decomposition using Loess), resolvem alguns dos pontos mencionados anteriormente.

Outros métodos de decomposição: X11

• X11
• Código
• Gráfico

• Desenvolvido pelo US Census Bureau.
• Baseado no modelo clássico, mas inclui outras etapas para superar as limitações do método original (a componente de tendência está disponível para todas as observações, a componente sazonal pode variar suavemente, etc).
• Existem versões tanto para o modelo aditivo quanto para o multiplicativo.
• É robusto a outliers.
• Mais detalhes desta metodologia podem ser encontrados em Dagum & Bianconcini (2016)
• Desenhando para dados mensais e quatrimestrais.
• No R o default é uma decomposição multiplicativa.

Code

library(seasonal)
library(tsibble)
library(fpp3)
passageiros %>%
  model(X_13ARIMA_SEATS(Passengers ~ x11())) %>% 
  components() %>%
  autoplot()

Outros métodos de decomposição: SEATS

• SEATS
• Código
• Gráfico

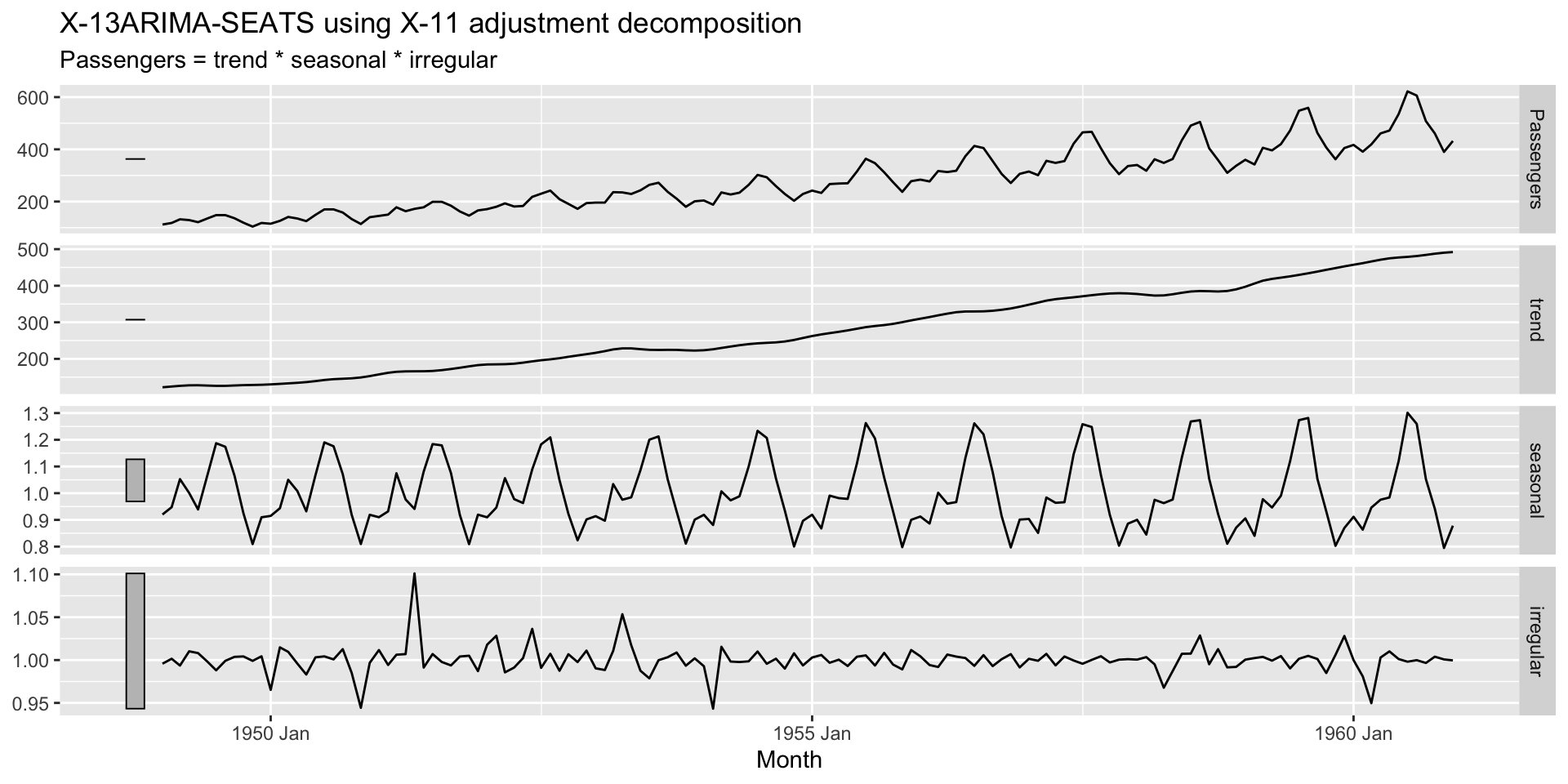
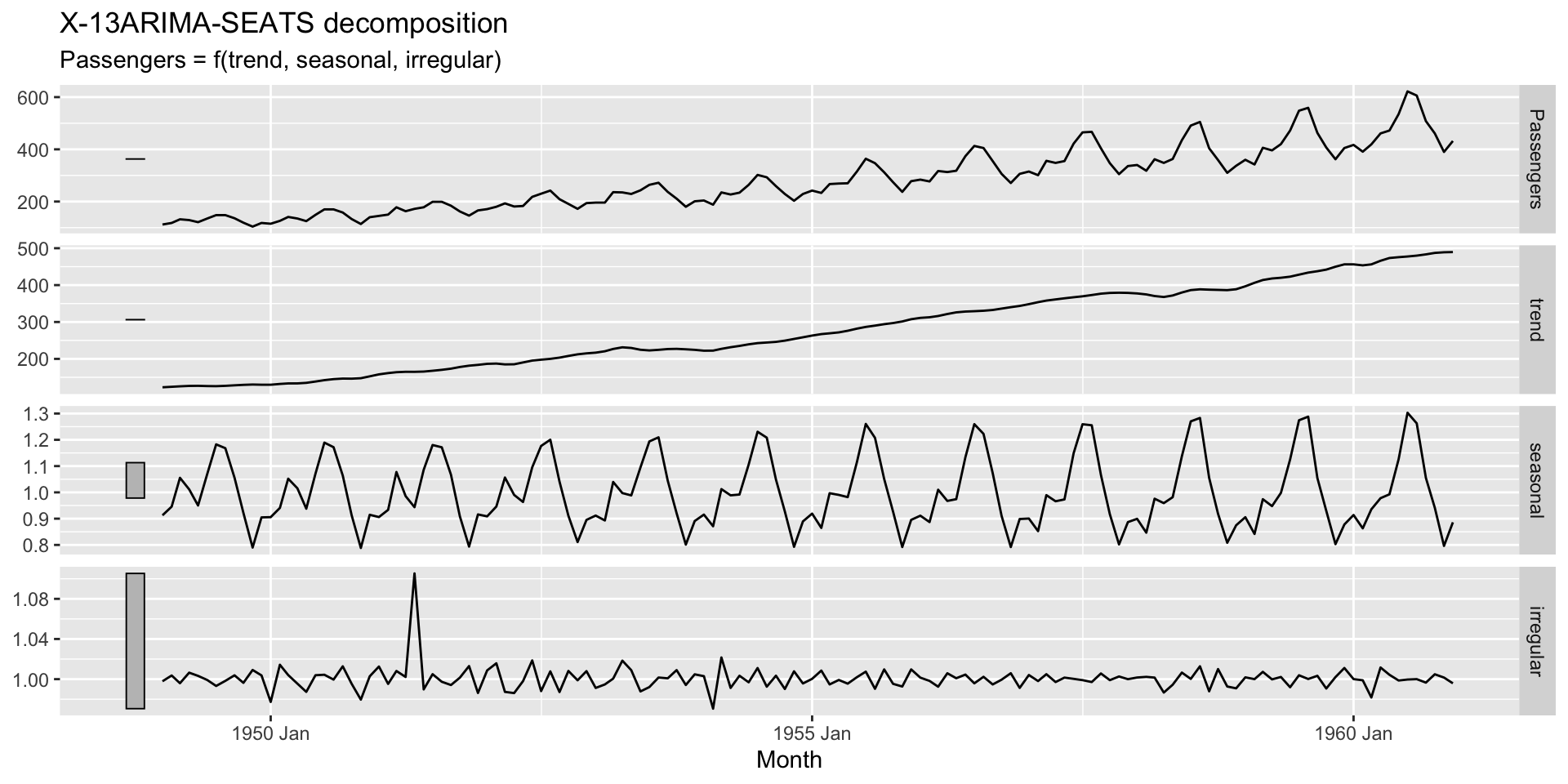
SEATS (Seasonal Extraction in ARIMA Time Series).

• Desenvolvido pelo banco de Espanha.
• Muito utilizado por agências governamentais no mundo todo.
• Desenhando para dados mensais e quatrimestrais.
• Mais detalhes desta metodologia podem ser encontrados em Dagum & Bianconcini (2016)

Code

passageiros %>%
  model(X_13ARIMA_SEATS(Passengers ~ seats())) %>% #<<
  components() %>%
  autoplot()

Outros métodos de decomposição: STL

• STL
• Código
• Gráfico

STL (Seasonal and Trend decomposition using Loess) ¹

• Desenvolvido por Cleveland (1990)
• Funciona com qualquer tipo de sazonalidade (não apenas mensal ou quatrimestral)
• A componente sazonal pode mudar ao longo do tempo.
• Pode ser robusto a observações atípicas (se especificarmos uma decomposição robusta).
• Útil para modelos aditivos
• Se quisermos aplicar o método em modelos multiplicativos, podemos aplicar um \(\log(\cdot)\).

Code

passageiros %>%
  model(STL(log(Passengers) ~ trend() + season(window = "periodic"), robust = TRUE)) %>% 
  components() %>%
  autoplot()

1. Loess é um método para estimar relações não lineares.

Previsão e decomposição

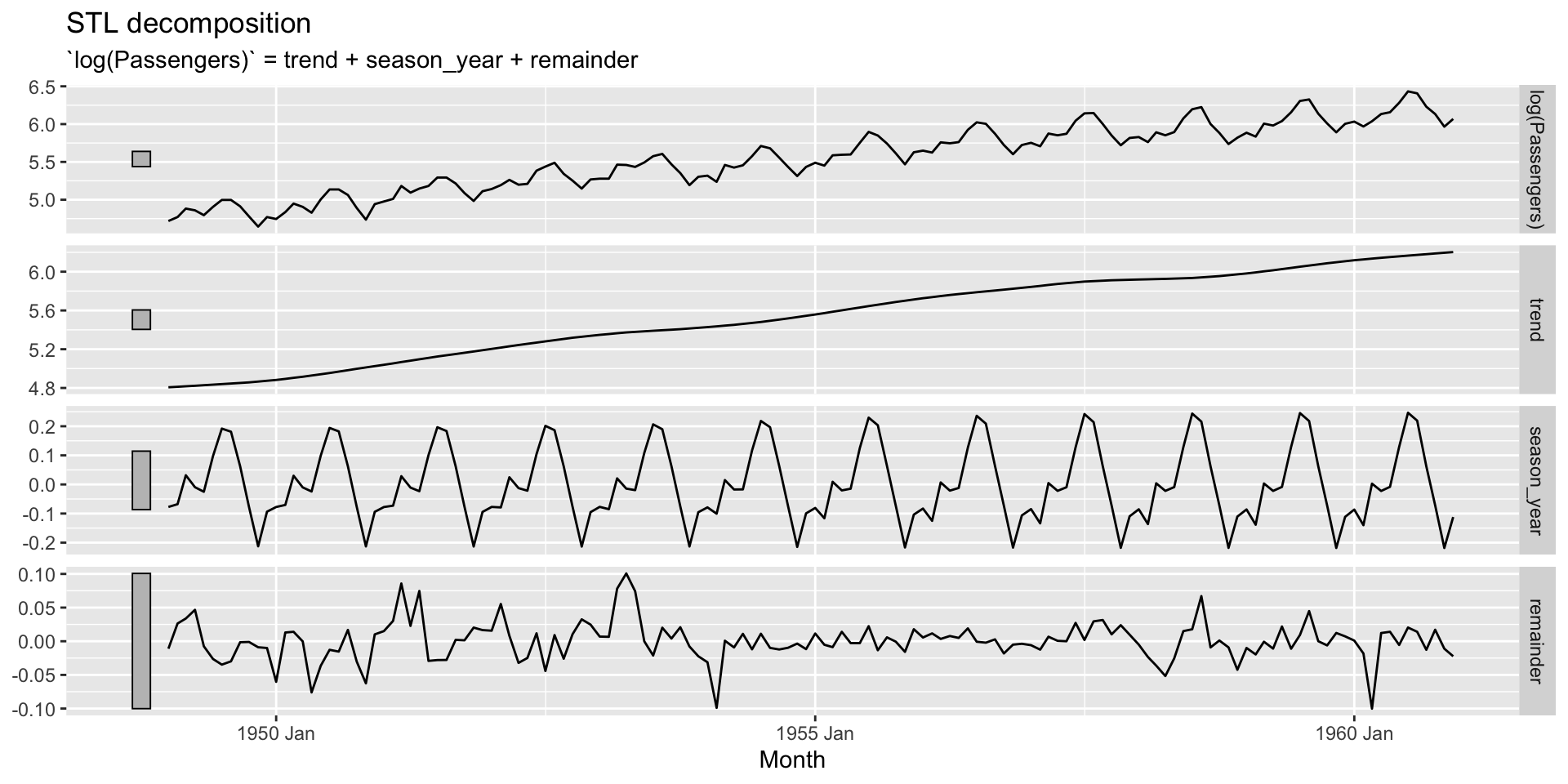
Métodos de decomposição são geralmente utilizados para entender a dinâmica da série mas também podem ser utilizados para fazer previsão.

Dependendo se o modelo for aditivo ou multiplicativo, podemos escrever a série temporal como.

\[y_t = \hat{S}_t + \underbrace{\hat{T}_t + \hat{R_t}}_{\hat{A}_t}\quad \text{ou} \quad y_t = \hat{S}_t \times \underbrace{\hat{T}_t \times \hat{R_t}}_{\hat{A}_t},\] em que \(\hat{A}_t\) é a série ajustada pela sazonalidade.

Para fazer previsão da série original, fazemos previsão da componente sazonal \(\hat{S}_t\) e da série ajustada pela sazonalidade \(\hat{A}_t\) de forma independente e depois combinamos ambas previsões para obter a previsão da série original.

Previsão e decomposição

• Comumente, um método ingênuo (naive) é utilizado para prever \(\hat{S}_t\) (utilizamos os valores de \(\hat{S}_t\) no último ano).
• Para prever \(\hat{A}_t\) utilizamos métodos para dados não sazonais (que veremos nas próximas aulas) como o método de Holt, ARIMA, etc.

Referências

• Hyndman, R.J., & Athanasopoulos, G. (2021). Forecasting: principles and practice, 3rd edition, OTexts: Melbourne, Australia. OTexts.com/fpp3.. Chapter 3.
• Brockwell, P.J & Davis, R.A. (2016). Introduction to Time Series and Forecasting, 3rd editions, Springer. Section 1.5
• Cleveland, R. B., Cleveland, W. S., McRae, J. E., & Terpenning, I. J. (1990). STL: A seasonal-trend decomposition procedure based on loess. Journal of Official Statistics, 6(1), 3–33. http://bit.ly/stl1990
• Dagum, E. B., & Bianconcini, S. (2016). Seasonal adjustment methods and real time trend-cycle estimation. Berlin/Heidelberg, Germany: Springer International Publishing.