Análise exploratória de dados - EDA

ME607 - Séries Temporais

Prof. Carlos Trucíos
ctrucios@unicamp.br

Instituto de Matemática, Estatística e Computação Científica (IMECC),
Universidade Estadual de Campinas (UNICAMP).

Introdução

Introdução

  • Como em todo projeto de análise de dados, análise exploratória de dados (EDA, em inglês) tem um papel fundamental.
  • EDA permitirá que identifiquemos padrões, dados atípicos, mudanças de comportamento em diferentes períodos, etc. Isto todo nos ajudará a escolher como abordar o problema.
  • Na aula de hoje focaremos em alguns gráficos, estatísticas e conceitos fundamentais relacionados com EDA em séries temporais.

Gráficos

Gráfico de sequência

Gráfico de sequência:

graficar todos os pontos (em ordem cronológica) unindo-os por segmentos de reta. No eixo \(X\) teremos o tempo e no eixo \(Y\) teremos os valores da séries temporal. Já temos visto este gráfico antes mas hoje aprenderemos alguns detalhes adicionais dele.

  • É o primeiro gráfico a ser feito quando trabalhamos com séries temporais.
  • Primeiro passo na EDA
  • Permite identificar observações atípicas.
  • Permite identificar mudanças ao longo do tempo.
  • Permite identificar diversos padrões nos dados.

Gráfico de sequência

Code 
library(dplyr)
library(tsibble)
library(ggplot2)
url <- "https://raw.githubusercontent.com/ctruciosm/ctruciosm.github.io/master/datasets/BTCUSDT.csv"
btc <- read.csv(url)
btc <- btc |> 
  select(timestamp, close) |> 
  mutate(timestamp = as.Date(timestamp)) |> 
  as_tsibble(index = timestamp)
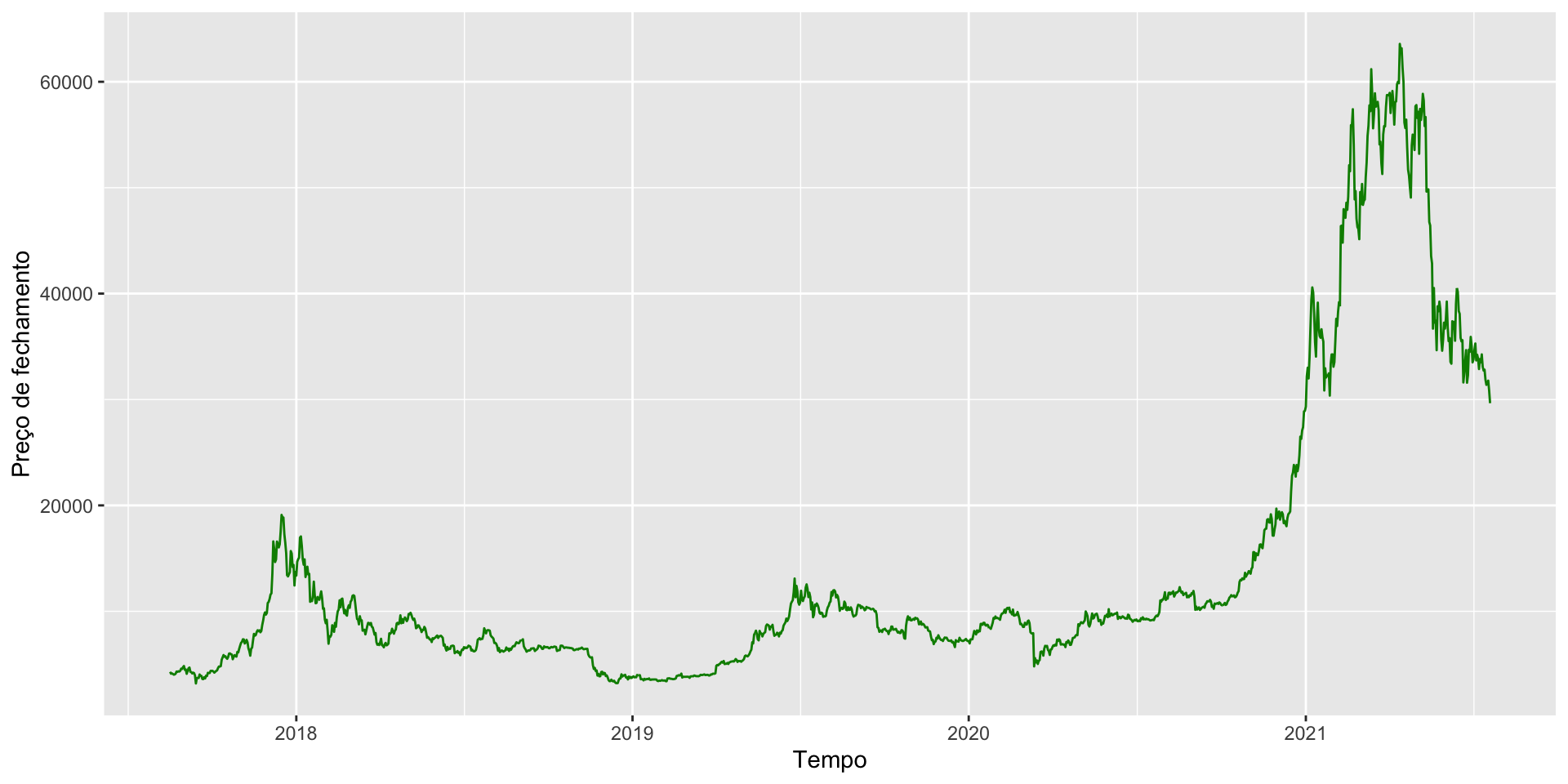
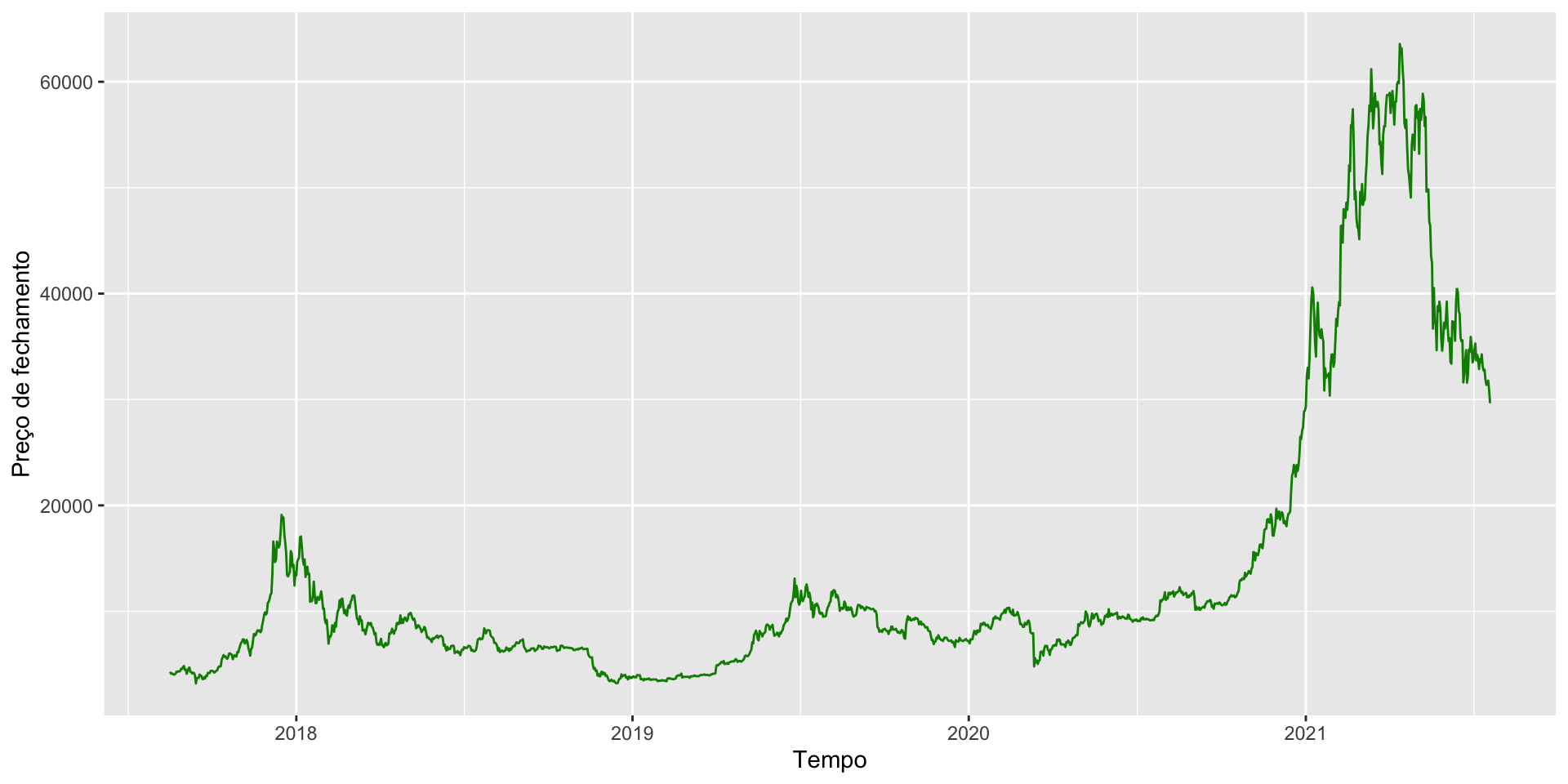
btc |> ggplot() + geom_line(aes(x = timestamp, y = close), color = "green4") +
  ylab("Preço de fechamento") + xlab("Tempo")

Code 
library(fpp3)
ansett |> filter(Airports == "ADL-PER", Class == "Economy") |> 
  autoplot(Passengers) + 
  labs(title = "Ansett airlines clase econômica",
       subtitle = "Adelaide(ADL) - Perth(PER)",
       y = "Número de passageiros",
       x = "Tempo")

Code 
library(fpp3)
PBS |> filter(ATC2 == "A10") |> 
  summarise(TotalC = sum(Cost)) |>
  mutate(Cost = TotalC/1e6) |> 
  autoplot(Cost) + 
  labs(title = "Medicamentos para diabetes na Austrália",
       y = "$ (milhões de dólares)",
       x = "Tempo")

Code 
btc |> mutate(retornos = log(close/lag(close))*100) |> 
  ggplot() + geom_line(aes(x = timestamp, y = retornos)) + 
  labs(title = "Bitcoin: retornos diários",
       y = "Retorno",
       x = "Tempo")

Padrões em séries temporais

Tendência

Dizemos que uma série apresenta tendência quando existe um incremento ou diminuição a longo prazo. A tendência não precisa ser linear.

Sazonalidade

Um padrão sazonal acontece quando o comportamento da série se repete segundo um fator sazonal (dia da semana, mês do ano, trimestre do ano, etc). A sazonalidade sempre acontece em um periodo fixo.

Ciclos

Um ciclo ocorre quando os dados apresentam subidas e quedas mas em uma frequência que não é fixa. Essas mudanças são explicadas pelas condições econômicas, climáticas, políticas, etc. A duração dessas flutuações é de, no mínimo, dois anos.

Identificar esses padrões é util para melhor escolher o modelo de séries temporais a ser utilizado.

Gráfico de sequência

  • Identificar a sazonalidade é muito importante na análise de séries temporais. Se encontrada, esta característica deverá ser incluida no modelo.
  • Uma forma simples de verificar sazonalidade é através de gráficos.

Gráficos sazonais

Code 
PBS |> filter(ATC2 == "A10") |> 
  summarise(TotalC = sum(Cost)) |>
  mutate(Cost = TotalC/1e6) |> 
  gg_season(Cost, labels = "both") + 
  labs(y = "$ (milhões)",
       title = "Gráfico sazonal: vendas de medicamentos para a diabetes")

Code 
vic_elec |>  gg_season(Demand, period = "day") +
  theme(legend.position = "none") +
  labs(y = "MWh", title = "Demanda de energía elétrica: Victoria, Austrália")

Code 
vic_elec |>  gg_season(Demand, period = "week") +
  theme(legend.position = "none") +
  labs(y = "MWh", title = "Demanda de energía elétrica: Victoria, Austrália")

Gráficos de dispersão

Code 
vic_elec |> 
  filter(year(Time) == 2014) |> 
  autoplot(Temperature) +
  labs(
    y = "Graus Celsius",
    title = "Temperatura (30 min)"
  )

Code 
vic_elec |> 
  filter(year(Time) == 2014) |> 
  autoplot(Demand) +
  labs(y = "Gigawatts",
       title = "Demanda energia elétrica (30 min)")

Code 
vic_elec |> 
  filter(year(Time) == 2014) |> 
  ggplot(aes(x = Temperature, y = Demand)) +
  geom_point() +
  labs(x = "Tempertura (graus Celsius)",
       y = "Demanda de energia (Gigawatts)")

Lag plots

Code 
aus_production  |> 
  filter(year(Quarter) >= 2000) |> 
  gg_lag(Beer, geom = "point") +
  labs(x = "lag(Beer, k)")

Autocovariância e autocorrelação

Autocovariância e autocorrelação

Para dois instantes quaquer (\(t\) e \(t+k\)), as funções de autocovariância e autocorrelação são dadas por: \[\gamma(t,t+k) = \mathbb{Cov}(Y_t, Y_{t+k}) = \mathbb{E}[(Y_t - \mu_t)(Y_{t+k}-\mu_{t+k})] \quad \text{e}\] \[\rho(t,t+k) = \mathbb{Cor}(Y_t, Y_{t+k}) = \dfrac{\mathbb{Cov}(Y_t, Y_{t+k})}{\sigma_t \sigma_{t+k}}\]

Se o processo for estacionário, temos que:

\[\gamma(t,t+k) = \mathbb{E}[(Y_t - \mu_t)(Y_{t+k}-\mu_{t+h})] =\mathbb{E}[(Y_t - \mu)(Y_{t+k}-\mu)] = \gamma(k) \quad \text{(pois independe de }t)\]

\[\rho(t,t+k) = \dfrac{\mathbb{Cov}(Y_t, Y_{t+k})}{\sigma_t \sigma_{t+k}} = \dfrac{\gamma(k)}{\sqrt{\gamma(0) \gamma(0)}} = \dfrac{\gamma(k)}{\gamma(0)} = \rho(k) \quad \text{(pois independe de }t)\]

Propriedades

  1. \(\gamma(0) \geq 0\)
  2. \(\gamma(k) = \gamma(-k)\)
  3. \(|\gamma(k)| \leq \gamma(0)\)
  4. \(-1 \leq \rho(k) \leq 1\)
  5. \(\gamma(k)\) é semidefinida positiva, no sentido que \(\displaystyle \sum_{i = 1}^n \sum_{j = 1}^n \alpha_i \alpha_j \gamma(t_j - t_i) \geq 0\) para quaisquer \(\alpha_i, \alpha_j \in \mathbb{R}\) e \(t_j -t_i \in \mathbb{Z}\).

Autocovariância amostral

Seja \(Y_1, \ldots, Y_n\) um processo estocástico estacionário. A autocovariância de \(Y_t\) com \(Y_{t+k}\) é dada por: \[\gamma(k) = \mathbb{E}[(Y_t-\mu)(Y_{t+k}-\mu)] = \mathbb{Cov}(Y_t, Y_{t+k})\]

Na prática, nunca conhecemos o processo estocástico todo, apenas uma realização. Assim, um estimador para \(\gamma(k)\) é dado por: \[\hat{\gamma}(k) = \dfrac{\displaystyle \sum_{t=1}^{n-k} (Y_t - \bar{Y})(Y_{t+k}-\bar{Y})}{n}.\]

Autocorrelação amostral

Seja \(Y_1, \ldots, Y_n\) um processo estocástico estacionário. A autocorrelação de \(Y_t\) com \(Y_{t+h}\) é dada por \[\rho(h) = \mathbb{Cor}(Y_t, Y_{t+h})\]

Na prática, nunca conhecemos o processo estocástico todo, apenas uma realização. Assim, um estimador para \(\rho(k)\) é dado por: \[\hat{\rho}(k) = \dfrac{\hat{\gamma}(k)}{\hat{\gamma}(0)}.\]

Autocovariância e autocorrelação são duas medidas de dependência em séries temporais. Autocorrelação tem a vantagem de que \(|\rho(k)| \leq 1\), o que facilita a interpretação.

Correlograma

As autocorrelações nos permitem graficar o correlograma (um gráfico que reporta as autocorrelações de \(y_t\) vs. \(y_{t-1}\), \(y_t\) vs. \(y_{t-2}\), \(y_t\) vs. \(y_{t-3}\), …)

  • O correlograma traz informação da correlação da série com ela mesma defasada no tempo.
  • Nos permitem identificar tendência: a correlação de \(y_t\) vs. \(y_{t-k}\) para pequenos valores de \(k\) tende a ser grande e positiva.
  • Nos permite identificar padrões sazonais: as autocorrelações serão maiores nos periodos sazonais (e múltiplos deste) do que em outros períodos. Além disso, o padrão (se algúm), repete-se.
  • Quando ambas caracteristicas são observadas, a função de autocorrelação é uma combinação de ambos os casos.

Correlograma

Code 
btc |> ACF(close, lag_max = 50) |> 
  autoplot()

O que diria da série? é estacionária?

Code 
aus_production  |> 
  filter(year(Quarter) >= 2000) |>  
  ACF(Beer, lag_max = 18) |> 
  autoplot() + labs(title = "Correlograma: produção trimestral de cerveja na Austrália")

O que diria da série? é estacionária?

Code 
x = rnorm(1000)
acf(x)

O que diria da série? é estacionária?

Correlograma

Code 
btc |> ggplot() + geom_line(aes(x = timestamp, y = close), color = "green4") +
  ylab("Preço de fechamento") + xlab("Tempo")

Code 
aus_production  |> 
  filter(year(Quarter) >= 2000) |> 
  select(Quarter, Beer) |> 
  autoplot()

Code 
dados <- data.frame(Tempo = 1:length(x), x) |> as_tsibble(index = Tempo)
dados |> autoplot()

Correlograma

Observações:

  1. A definição de \(\hat{\gamma}(k) = n^{-1} \displaystyle \sum_{t = 1}^{t-k} (y_{t + k} - \bar{y})(y_t - \bar{y})\) é preferida (em lugar de utilizar \((n - k)^{-1}\)) pois \(\forall\) \(k \geq 1\), a matriz de covariância amostral \(\hat{\Gamma}_k\) é semidefinida positiva, em que \[\hat{\Gamma}_k = \begin{bmatrix} \hat{\gamma}_0 & \hat{\gamma}_1 & \cdots & \hat{\gamma}_{k-1} \\ \hat{\gamma}_1 & \hat{\gamma}_0 & \cdots & \hat{\gamma}_{k-2} \\ \vdots & \cdots & \ddots & \vdots \\ \hat{\gamma}_{k-1} & \hat{\gamma}_{k-2} & \cdots & \hat{\gamma}_{0} \\ \end{bmatrix}\]

Correlograma

Observações:

  1. As linhas azuis tracejadas no correlograma são bandas de confiança e são obtidas como \(\pm z_{\alpha/2}\dfrac{1}{\sqrt{n}}\) (voltaremos a este ponto mais adiante).
  2. Uma forma simples de verificar se a \(k\)-ésima autocorrelação (\(\rho(k)\)) é significativa, é ver se \(\hat{\rho}(k)\) está fora das bandas de confiança.

Autocorrelação parcial

Autocorrelação parcial

  • Embora a autocorrelação entre \(Y_t\) e \(Y_{t+k}\) seja de vital importância em um contexto de séries temporais. Podemos estar interessados em calcular a autocorrelação entre \(Y_t\) e \(Y_{t+k}\) uma vez que temos removido o efeito da dependência linear de \(Y_{t+1}, \cdots, Y_{t+k-1}\)
  • Este tipo de correlação é conhecido como autocorrelação parcial e é dado por \[\phi_{kk} = \mathbb{C}or(Y_t, Y_{t+k}| Y_{t+1}, \cdots, Y_{t+k-1}).\]
  • Pode-se provar que \[\phi_{11} = \rho_1 \quad e \quad \phi_{kk} = \begin{vmatrix} 1 & \rho_1 & \rho_2 & \cdots & \rho_{k-2} & \rho_{1}\\ \rho_1 & 1 & \rho_1 & \cdots & \rho_{k-3} & \rho_{2}\\ \vdots & \vdots & \vdots & \cdots & \vdots & \vdots\\ \rho_{k-1} & \rho_{k-2} & \rho_{k-3} & \cdots & \rho_{1} & \rho_k\\ \end{vmatrix} \begin{vmatrix} 1 & \rho_1 & \rho_2 & \cdots & \rho_{k-2} & \rho_{k-1}\\ \rho_1 & 1 & \rho_1 & \cdots & \rho_{k-3} & \rho_{k-2}\\ \vdots & \vdots & \vdots & \cdots & \vdots & \vdots\\ \rho_{k-1} & \rho_{k-2} & \rho_{k-3} & \cdots & \rho_{1} & 1\\ \end{vmatrix}^{-1}\]

Ergodicidade

Ergodicidade

  • Séries estacionárias são caracterizadas pela média \(\mu\), variância \(\sigma^2\), autocorrelações \(\rho(k)\).
  • Se conhecessemos todas as possíveis realizações do processo estocástico, poderiamos calcular com exatidado esses valores.
  • Bastariam apenas algumas realizações do processo estocásticos para estimar os parâmetros de interesse.
  • Na prática não observamos multiples realizações mas apenas uma relização.
  • Para séries estacionárias, sob algumas condições, podemos estimar os parâmetros de interesse com a única realização e ainda termos boas propriedades estatísticas.

Ergodicidade

Até agora temos que:

  • Um estimador para \(\mu\) é \(\bar{Y} = n^{-1} \displaystyle \sum_{i = 1}^n Y_i\)
  • Um estimador para \(\gamma(k)\) é \(\hat{\gamma}{(k)} = n^{-1} \displaystyle \sum_{t=1}^{n-k} (Y_t - \bar{Y})(Y_{t+k}-\bar{Y})\)
  • Um estimador para \(\rho(k)\) é \(\hat{\rho}(k) = \hat{\gamma}(k) / \hat{\gamma}(0)\)

Será que esses estimadores possuem boas propriedades estatísticas?

Ergodicidade

\[\bar{Y} = \frac{\displaystyle \sum_{i = 1}^n Y_i}{n}\]

  • \(\mathbb{E}(\bar{Y}) = \dfrac{1}{n}\displaystyle \sum_{i = 1}^n \mathbb{E}(Y_i) = \dfrac{n\mu}{n} = \mu\)
  • \(\mathbb{V}(\bar{Y}) = \dfrac{1}{n^2} \displaystyle \sum_{i = 1}^n \sum_{j = 1}^n \mathbb{C}ov(Y_i, Y_j) = \dfrac{\gamma(0)}{n^2} \displaystyle \sum_{i = 1}^n \sum_{j = 1}^n \rho(j-i) = \dfrac{\gamma(0)}{n} \displaystyle \sum_{k = -(n-1)}^{n-1} \big(1 - \dfrac{|k|}{n}\big)\rho(k)\)

Note que se \(\lim_{n \rightarrow \infty}\displaystyle \sum_{k = -(n-1)}^{n-1} \big(1 - \dfrac{|k|}{n}\big)\rho(k) < \infty\), então \(\mathbb{V}(\bar{Y}) \rightarrow_{n \rightarrow \infty} 0\) e \(\bar{Y} \rightarrow_p \mu.\)

Ergodicidade

Definição

Um processo estacionário é ergódico para o primeiro momento se \[\bar{Y} \rightarrow_p \mu.\]

Definição

Um processo estacionário é ergódico para o segundo momento se \[\hat{\gamma}(k) = \dfrac{1}{n} \displaystyle \sum_{i = 1}^{n-k}(Y_t - \bar{Y})(Y_{t+k}- \bar{Y})\rightarrow_p \gamma(k)\]

Ergodicidade permite que, utilizando uma única realização do processo, possamos estimar os parâmetros do processo estocástico todo.

Ruido branco

Ruido branco

Ruido branco

Coleção de variáveis aleatórias com médias zero, variância constante e que além disso são não correlacionadas.

Ruido branco

Um processo \(\{ \epsilon_t \}\) é chamado de ruido branco se é uma sequência de variáveis aleatórias da distribuição fixa com \(\mathbb{E}(\epsilon_t) = 0\), \(\mathbb{V}(\epsilon_t) = \sigma^2\) e \(\gamma(k) = 0 \quad \forall k\).

Como verificar se estamos ante um ruido branco?

Pode-se provar que se o processo for ruido branco, então \[\rho(k) \rightarrow^D N\big(0, \dfrac{1}{n}\big) \quad e \quad \phi_{kk} \rightarrow^D N\big(0, \dfrac{1}{n}\big)\]

Referências

Carlos Trucíos (IMECC/UNICAMP) | ME607 - Séries Temporais | ctruciosm.github.io