Introdução e conceitos básicos

ME607 - Séries Temporais

Prof. Carlos Trucíos
ctrucios@unicamp.br

Instituto de Matemática, Estatística e Computação Científica (IMECC),
Universidade Estadual de Campinas (UNICAMP).

Introdução

Se pudéssemos saber primeiro onde estamos e para onde vamos, poderíamos julgar melhor o que fazer e como fazê-lo. Abraham Lincoln

O interesse em fazer previsão existe em muitas situações: prever a demanda de um produto, prever a quantidade de megas que serão utilizados nos próximos dias, prever o preço/volatilidade das ações, prever a velocidade do vento, etc.

A previsibilidade de um evento depende de vários fatores, entre eles:

Quantos dados estão disponíveis.
Que tanto conhecemos os fatores que contribuen para fazer a previsão.
Que tão semelhante é o futuro do passado.
Se a previsão afeta o que estamos tentanto prever.

Poderia dar algum exemplo em que todos/alguns desses fatores são satisfeitos?

Introdução

Caso 1: Demanda residencial de eletricidade (curto prazo)

Geralmente, há vários anos de dados sobre a demanda por eletricidade disponíveis e muitas décadas de dados sobre as condições climáticas.
Temos uma boa ideia dos fatores contribuintes: a demanda por eletricidade é impulsionada em grande parte pelas temperaturas, com efeitos menores para variações de calendário, como feriados e condições econômicas.
Para previsões de curto prazo (até algumas semanas), é seguro assumir que o comportamento da demanda será semelhante ao que foi visto no passado.
Para a maioria dos usuários residenciais, o preço da eletricidade não depende da demanda e, portanto, as previsões de demanda têm pouco ou nenhum efeito no comportamento do consumidor.

Introdução

Caso 2: Taxas da câmbio

Muitos dados disponíveis: geralmente temos um histórico de dados contendo décadas de informação.
Temos uma compreensão limitada dos fatores que afetam as taxas de câmbio
O futuro pode muito bem ser diferente do passado se houver uma crise financeira ou política em um dos países
As previsões da taxa de câmbio têm um efeito direto nas próprias taxas: se houver previsões bem divulgadas de que a taxa de câmbio aumentará, então as pessoas ajustarão imediatamente o preço que estão dispostas a pagar afetando exatamente o que estamos tentando prever.

Introdução

Em qual dos casos (1 ou 2),

vocês acham que conseguiremos construir

um bom modelo de previsão?

(Justifique sua resposta)

Introdução

Previsão pode ser feita utilizando métodos ingênuos (como repetir a última observação ou apenas utilizar a média histórica) ou métodos mais complexos (como métodos estatísticos avançados, aprendizado de máquina e redes neurais).

Previsão ajuda às organizações a tomarem melhores decisões e fornece uma guia para o planejamento de médio e longo prazo. É por isso que saber lidar com séries temporais é de vital importância.

Observação:

\[\text{Previsão} \neq \text{Metas} \neq \text{Planejamento}\]

Introdução

\[\text{Previsão} \neq \text{Metas} \neq \text{Planejamento}\]

Previsão: dadas todas as informações disponíveis (historico, outras variáveis, conhecimento sobre eventos futuro que possam afetar a previsão), queremos prever o futuro com a maior acurácia possível.
Metas: aquilo que gostariamos que aconteça (mas não necessáriamente acontece)
Planejamento: ações necessárias para que as previsões alcancem às metas.

Estamos interessados em previsões a curto, médio e longo prazo.

Embora existam métodos qualitativos para fazer previsão quando não temos historico de dados (ver Cap 6 de Hyndman e Athanasopoulos (2021)), focaremos no caso em que possuimos um conjunto de dados históricos e é razoável pensar que algums padrões aprendidos do passado continurão acontecendo.

Introdução

Em qualquer projeto envolvendo previsão precisamos determinar qual é nosso interesse:

Estamos interessados nas vendas de uma loja ou de todas as lojas de uma região?
Estamos interessados em dados diários, semanais, mensais, anuais?
Estamos interessados na demanda de um produto ou um grupo de produtos?
Qual é o horizonte de previsão?
Com que frequência precisaremos fazer a previsão?

Responder corretamente a essas perguntas nos ajudará na escolha da abordagem a ser utilizada.

Séries temporais: Overview

Séries temporal: a grosso modo, todo processo que é observado sequencialmente ao longo do tempo é uma série temporal.

Quando as observações são igualmente espaçadas (diário, semanal, mensal, etc) dizemos que a série temporal é regular. Caso contrário, é chamada de irregular.

Exemplos

Produto interno bruto (anual) do Brasil.
Preço diário do Bitcoin.
Vendas semanais de um produto.
Temperatura diária em Campinas.
Consumo mensal de energia/agua.
Gasto mensal familiar com futilidades.
etc

Séries temporais: Overview

Nesta disciplina, aprenderemos como analisar séries temporais como as vistas anteriormente, ou seja, séries temporais regulares.

Séries temporais: Overview

Análise de Séries Temporais

É o processo de extrair insights (relevantes) a partir de dados de séries temporais, explorando a estrutura e as características da série, bem como identificando padrões que podem ser utilizados para prever valores/eventos futuros da série.

Este processo, pode ser resumido nos seguintes 4 passos:

Coleta de dados: extração de dados de diferentes fontes (csv, sql, txt, xlsx, etc)
Preparação de dados: limpeza, transformação, agregação e reformatação de dados brutos (não estruturados)
Análise descritiva: EDA (Tabelas, Gráficos, estatísticas resumo) para extrair insights dos dados
Análise preditiva: aplicação de métodos estatísticos para prever eventos futuros

Séries temporais: Overview

Observação

Alguns autores também incluem na preparação de dados os métodos para lidar com dados faltantes e outliers. Contudo, nos dias de hoje existem métodos mais complexos que lidam com estes problemas sem precisar preencher dados faltantes ou remover outliers. Ver, por exemplo:

Cascone, M. H., & Hotta, L. K. (2019). Quasi-maximum likelihood estimation of GARCH models in the presence of missing values. Journal of Statistical Computation and Simulation, 89(2), 292–314.
Wee, D. C., Chen, F., & Dunsmuir, W. T. (2023). Estimating GARCH (1, 1) in the presence of missing data. The Annals of Applied Statistics, 17(3), 2596-2618.
Abbara, O., & Zevallos, M. (2022). Stochastic volatility with missing data: Assessing the effects of holidays. Communications in Statistics: Case Studies, Data Analysis and Applications, 8(3), 423-433.
Hotta, L. K., & Trucíos, C. (2018). Inference in (M) GARCH models in the presence of additive outliers: specification, estimation, and prediction. Advances in Mathematics and Applications: Celebrating 50 years of the Institute of Mathematics, Statistics and Scientific Computing, University of Campinas, 179-202.
Trucíos, C., Hotta, L. K., & Ruiz, E. (2017). Robust bootstrap forecast densities for GARCH returns and volatilities. Journal of Statistical Computation and Simulation, 87(16), 3152-3174.
etc

Séries temporais: Overview

Quando falamos em previsão, o objetivo é estimar como a sequência de observações (observadas cronologicamente) continuará no futuro.

\[y_t = f(X_{1}, \cdots, X_{k}, u)\]

\[y_t = f(y_{t-1}, \cdots, y_{t-r}, u)\]

\[y_t = f(y_{t-1}, \cdots, y_{t-r}, X_1, \cdots, X_k, u)\]

Séries temporais: Overview

Após da definição do problema (que não é algo trivial), o processo de modelagem de séries temporais apresenta o seguinte fluxo.

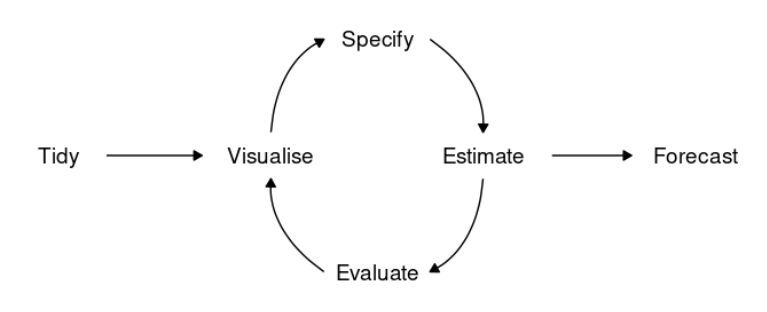
Fonte: Livro ‘Forecasting: Principles and Practice’

Tidy: Precisamos coletar e preparar os dados para podermos utilizar os diversos modelos implementados.
Visualise: Fazer o gráfico da série temporal é muito importante e da os primeiros insights do que deve ser feito.
Especificar, estimar e avaliar o modelo. (Modelagem)
Fazer previsões.

Conceitos básicos

Processo Estocástico

Uma coleção de variáveis aleatórias \(\{ Y_t \}\) indexada pelo tempo \(t\) é chamado de processo estocástico.

Série Temporal

Uma realização (\(\{y_t\}\)) de um processo estocástico é chamado de série temporal.

Na prática nunca observamos o processo estocástico, mas apenas uma realização do processo.

É muito comum chamar de série temporal tanto ao processo estocástico quando à realização do processo.

Ruido branco

Coleção de variáveis aleatórias com médias zero, variância constante e que além disso são não correlacionadas.

Conceitos básicos

Na Figura 1 temos um exemplo da realização de um processo estocástico. Consegue identificar/explicar o conceito de processo estocástico na mesma figura?

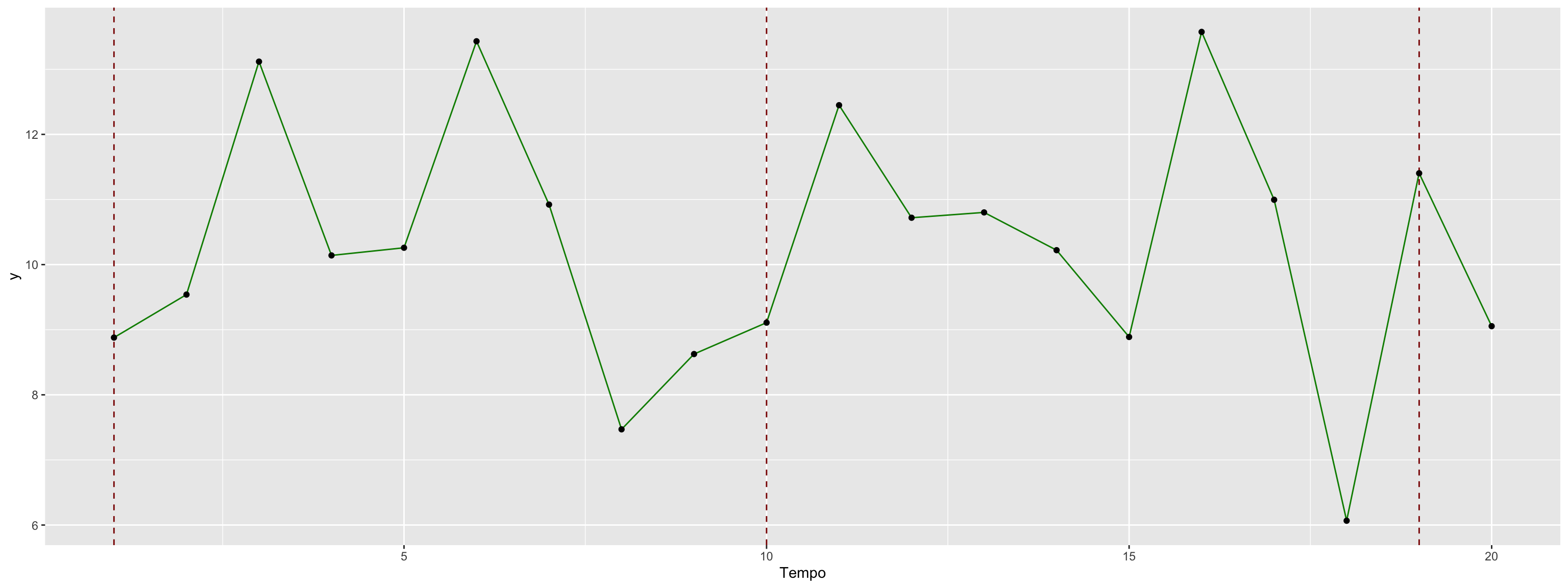
Figura 1: Exemplo de série temporal e processo estocástico.

Conceitos básicos:

Função de médias: para cada instante \(t\), \(\mu_t = \mathbb{E}(Y_t).\)
Função de variâncias: para cada instante \(t\), \(\sigma_t^2 = \mathbb{V}(Y_t).\)
Função de autocovariância e autocorrelação: para dois instantes quaisquer (\(t\) e \(t+h\)), as funções de autocovariância e autocorrelação são dadas por: \[\gamma(t,t+h) = \mathbb{Cov}(Y_t, Y_{t+h}) = \mathbb{E}[(Y_t - \mu_t)(Y_{t+h}-\mu_{t+h})] \quad \text{e}\] \[\rho(t,t+h) = \mathbb{Cor}(Y_t, Y_{t+h}) = \dfrac{\mathbb{Cov}(Y_t, Y_{t+h})}{\sigma_t \sigma_{t+h}}\]

Obs: como o processo estocástico é uma coleção de variáveis aleatórias \(\{Y_t \}\) indexadas pelo tempo \(t\), para cada \(t\) temos que \(Y_t\) tem sua própria distribuição (e então faz sentido pensar na esperança, variância, …).

Conceitos básicos

Processo estritamente estacionário

Um processo estocástico \(\{Y_t\}_{t = -\infty}^{\infty}\) é dito estritamente estacionário se todas as distribuições finito dimensionais permanecem as mesmas sob translações do tempo, ou seja, \[F_{y_{t_1}, \cdots, y_{t_k}}(x_1, \cdots, x_k) = F_{y_{t_1 + h}, \cdots, y_{t_k + h}}(x_1, \cdots, x_k), \quad \forall h\]

Conceitos básicos

Processo (fracamente) estacionário

Um proceso estocástico \(\{Y_t\}_{t = -\infty}^{\infty}\) é dito fracamente estacionário (estacionário de segunda ordem ou simplesmente estacionário) se:

\(\mathbb{E}(Y_t^2) < \infty, \quad \forall t\)
\(\mathbb{E}(Y_t) = \mu_t = \mu, \quad \forall t\)
\(\mathbb{Cov}(Y_t, Y_{t+h})\) depende somente de \(h\) e não de \(t\).

Conceitos básicos

Note que a primeira condição dos processos estacionários afirma que o segundo momento deve ser finito (mesmo que diferente em diferentes períodos do tempo).
A segunda condição afirma que a média é igual para todo o período.
A terceira condição estabelece que variância é constante para todo o período e que a autocovariância depende apenas de \(h\) e não do tempo (\(t\)).

Se a série satisfaz essas condições é dita de estacionária, caso contrário é dita de não estacionária.

Visualmente, observa-se estacionaridade se uma série flutua em torno de uma média fixa e se a variância da série é constante ao longo do tempo. Contudo, são necessários testes de hipóteses para verificar ou não a estacionaridade da série.

Conceitos básicos

Qual das seguintes séries parece ser estacionária?

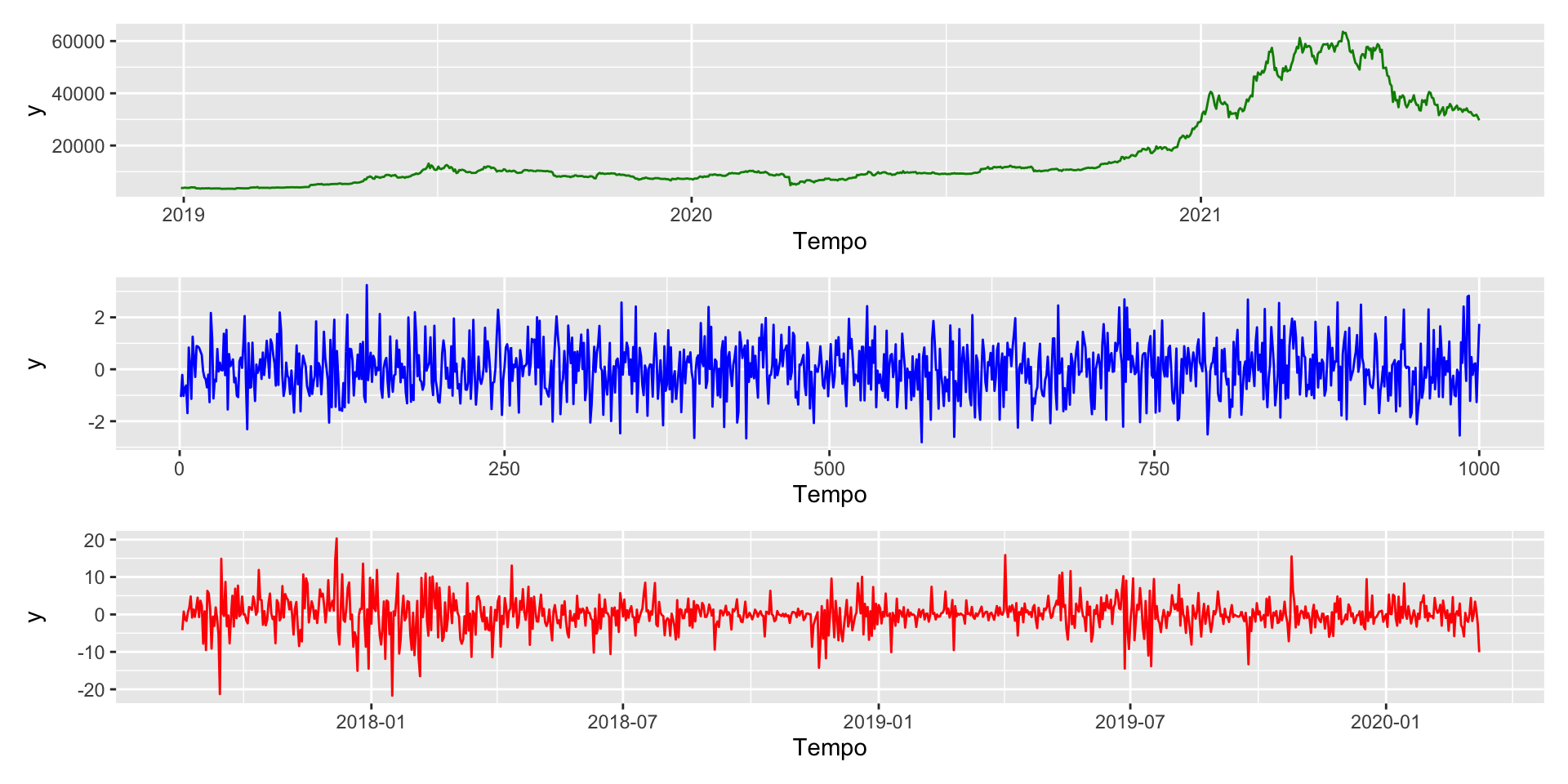
Referências

Hyndman, R.J., & Athanasopoulos, G. (2021). Forecasting: principles and practice, 3rd edition, OTexts: Melbourne, Australia. OTexts.com/fpp3.. Chapter 1.
Bueno, R.D.L.S (2011). Econometria de Séries Temporais, 2ed, CENGAGE. São Paulo, Brasil. Capítulo 2.

Trabalho

O trabalho do curso consiste em analisar uma série temporal, aplicar os conhecimentos adquiridos ao longo da disciplina é, se for preciso, recorrer a métodos mais avançados para melhorrar o ajuste e previsão.

As séries devem ser Brasileiras.
Devem ser séries regulares.
Vocês deverão apresentar no final das aulas, a série escolhida, apresentando uma breve EDA (até receber o OK do professor sobre a série escolhida)
O trabalho é em grupo de até 4 integrantes
Serão 3 apresentações ao longo do semestre, recebendo feedback nas duas primeiras para se prepararem para o trabalho final.