Modelos de Regressão e Previsão (ACA228)

class: center, middle, inverse, title-slide

# Modelos de Regressão e Previsão (ACA228)
## Suavização Exponencial
### Prof. Carlos Trucíos <br><a href="http://ctruciosm.github.io"> <i class="fa fa-desktop fa-fw"></i>  ctruciosm.github.io</a><br> <a href="mailto:carlos.trucios@facc.ufrj.br"><i class="fa fa-paper-plane fa-fw"></i>  carlos.trucios@facc.ufrj.br</a><br>
### Faculdade de Administração e Ciências Contábeis, </br> Universidade Federal de Rio de Janeiro

---

layout: true

<a class="footer-link" href="http://ctruciosm.github.io">ctruciosm.github.io &mdash; Carlos Trucíos (FACC/UFRJ)</a>

---

<div>
<style type="text/css">.xaringan-extra-logo {
width: 200px;
height: 350px;
z-index: 0;
background-image: url(imagens/UFRJ.png);
background-size: contain;
background-repeat: no-repeat;
position: absolute;
top:1em;right:1em;
}
</style>
<script>(function () {
  let tries = 0
  function addLogo () {
    if (typeof slideshow === 'undefined') {
      tries += 1
      if (tries < 10) {
        setTimeout(addLogo, 100)
      }
    } else {
      document.querySelectorAll('.remark-slide-content:not(.title-slide):not(.inverse):not(.hide_logo)')
        .forEach(function (slide) {
          const logo = document.createElement('div')
          logo.classList = 'xaringan-extra-logo'
          logo.href = null
          slide.appendChild(logo)
        })
    }
  }
  document.addEventListener('DOMContentLoaded', addLogo)
})()</script>
</div>

## Introdução

- Proposto nos 1950s

- É uma média ponderada das últimas observações. Observações mais recentes recebem um peso maior do que observações mais "antigas".

- Fornece previsões de uma forma rápida e são uma alternativa útil na prática.

- Estudaremos alguns dos mais famosos métodos de suavização exponencial.

---
class: inverse, right, middle
# Suavização Exponencial Simples
---

## Suavização Exponencial Simples

- Utilizado quando a série temporal não tem um padrão claro de tendência e/ou sazonalidade. Por exemplo:

![](ACA228_ST_06_files/figure-html/unnamed-chunk-1-1.png)

Com este método, a previsão um passo à frente é obtida através de:

`$$\hat{y}_{T+1|T} = \alpha y_{T} + \alpha (1-\alpha) y_{T-1} + \alpha (1-\alpha)^2 y_{T-2} + \ldots,$$` em que `$0 \leq \alpha \leq 1$` é o parâmetro de suavização.

---

## Suavização Exponencial Simples

`$$\hat{y}_{T+1|T} = \alpha y_{T} + \alpha (1-\alpha) y_{T-1} + \alpha (1-\alpha)^2 y_{T-2} + \ldots,$$`

- Se `$\alpha \approx 0$`, as observações mais atigas recebem um peso maior.

- Se `$\alpha \approx 1$`, as observações mais recentes recebem um peso maior.

- Se `$\alpha = 1$`, o método se reduz ao método NAIVE, `$\hat{y}_{T+1|T} = y_T$`.

De forma alternativa, podemos utilizar uma forma recursiva e escrever:

- `$\hat{y}_{T+1|T} = \alpha y_T + (1-\alpha) \hat{y}_{T|T-1},$`
- `$\hat{y}_{T|T-1} = \alpha y_{T-1} + (1-\alpha) \hat{y}_{T-1|T-2},$`
- `$\vdots$`
- `$\hat{y}_{3|2} = \alpha y_2 + (1-\alpha) \hat{y}_{2|1},$`
- `$\hat{y}_{2|1} = \alpha y_1 + (1-\alpha) l_0,$`

> Em que `$l_0$` precisa ser estimado (assim como `$\alpha$`).

---

## Suavização Exponencial Simples

Assim como nos modelos de regressão, precisamos estimar alguns parâmetros. Neste caso precisamos estimar `$\alpha$` e `$l_0$`.

Para obter os valores estimados `$\hat{\alpha}$` e `$\hat{l}_0$`, vamos a minimizar a soma de quadrados dos resíduos, ou seja:

`$$SQE = \displaystyle \sum_{t=1}^T (\underbrace{y_t - \hat{y}_{t|t-1}}_{e_t})^2 = \sum_{t=1}^T e_t^2$$`

- A diferença de regressão por MQO, desta vez a solução não tem forma fechada e precisaremos de métodos numéricos para encontrá-la. Na pratica, isto não será problema, utiliaremos a função `ETS()` do **R** para ajustar o modelo.

---

## Suavização Exponencial Simples

.panelset[
.panel[.panel-name[Dados]

```r
library(fpp3)
algeria_economy <- global_economy %>% filter(Country == "Algeria")
glimpse(algeria_economy)
```

```
## Rows: 58
## Columns: 9
## Key: Country [1]
## $ Country    <fct> "Algeria", "Algeria", "Algeria", "Algeria", "Algeria", "Alg…
## $ Code       <fct> DZA, DZA, DZA, DZA, DZA, DZA, DZA, DZA, DZA, DZA, DZA, DZA,…
## $ Year       <dbl> 1960, 1961, 1962, 1963, 1964, 1965, 1966, 1967, 1968, 1969,…
## $ GDP        <dbl> 2723648552, 2434776646, 2001468868, 2703014867, 2909351793,…
## $ Growth     <dbl> NA, -13.605441, -19.685042, 34.313729, 5.839413, 6.206898, …
## $ CPI        <dbl> NA, NA, NA, NA, NA, NA, NA, NA, NA, 2.569025, 2.738580, 2.8…
## $ Imports    <dbl> 67.14363, 67.50377, 20.81865, 36.82552, 29.43976, 25.83308,…
## $ Exports    <dbl> 39.04317, 46.24456, 19.79387, 24.68468, 25.08406, 22.60394,…
## $ Population <dbl> 11124888, 11404859, 11690153, 11985136, 12295970, 12626952,…
```
]
.panel[.panel-name[Gráfico]

```r
algeria_economy %>% autoplot(Exports)
```

![](ACA228_ST_06_files/figure-html/unnamed-chunk-3-1.png)
Sem tendência nem sazonalidade, canditato perfeito para usar suavização exponencial.
]
.panel[.panel-name[Modelo]

```r
modelo <- algeria_economy %>%
  model(ETS(Exports ~ error("A") ))
report(modelo)
```

```
## Series: Exports 
## Model: ETS(A,N,N) 
##   Smoothing parameters:
##     alpha = 0.8399875 
## 
##   Initial states:
##    l[0]
##  39.539
## 
##   sigma^2:  35.6301
## 
##      AIC     AICc      BIC 
## 446.7154 447.1599 452.8968
```

```r
fore_algeria <- modelo %>% forecast(h = 6)
```
**Obs: "A" para aditivo e "M" para multiplativo**
]
.panel[.panel-name[Gráfico]

```r
fore_algeria %>% autoplot(algeria_economy) +
  geom_line(aes(y = .fitted), color = "red",  data = augment(modelo)) 
```

![](ACA228_ST_06_files/figure-html/unnamed-chunk-5-1.png)
]
]

---
class: inverse, right, middle
# Método de Holt
---

## Método de Holt (1957)

- Utilizado quando a série apresenta tendência.

- A previsão envolve duas equações de suavização: uma para o nível e outra para a tendência.

`$$\text{Previsão:} \quad \hat{y}_{t+h|t} = l_t + h b_t,$$`
`$$\text{Equação do Nível:} \quad l_t = \alpha y_t + (1 - \alpha) (l_{t-1} + b_{t-1}),$$`
`$$\text{Equação de Tendência:} \quad  b_t = \beta (l_t - l_{t-1})  + (1-\beta) b_{t-1}.$$`

Em que `$0 \leq \alpha \leq 1$` e `$0 \leq \beta \leq 1$`. Note que, no instante `$t=1$` precisaremos de `$l_0$` e `$b_0$`

---

## Método de Holt (1957)

.panelset[
.panel[.panel-name[Dados]

```r
library(fpp3)
australia_economy <- global_economy %>% filter(Country == "Australia") %>% 
  mutate(Pop = Population / 1e6) # População em milhoes 1e6 = 10^6
glimpse(australia_economy)
```

```
## Rows: 58
## Columns: 10
## Key: Country [1]
## $ Country    <fct> "Australia", "Australia", "Australia", "Australia", "Austra…
## $ Code       <fct> AUS, AUS, AUS, AUS, AUS, AUS, AUS, AUS, AUS, AUS, AUS, AUS,…
## $ Year       <dbl> 1960, 1961, 1962, 1963, 1964, 1965, 1966, 1967, 1968, 1969,…
## $ GDP        <dbl> 18573188487, 19648336880, 19888005376, 21501847911, 2375853…
## $ Growth     <dbl> NA, 2.4856050, 1.2964777, 6.2142784, 6.9787237, 5.9834500, …
## $ CPI        <dbl> 7.960458, 8.142560, 8.116545, 8.168574, 8.402706, 8.688866,…
## $ Imports    <dbl> 14.06175, 15.02508, 12.63093, 13.83405, 13.76450, 15.26734,…
## $ Exports    <dbl> 12.99445, 12.40310, 13.94301, 13.00589, 14.93825, 13.22018,…
## $ Population <dbl> 10276477, 10483000, 10742000, 10950000, 11167000, 11388000,…
## $ Pop        <dbl> 10.27648, 10.48300, 10.74200, 10.95000, 11.16700, 11.38800,…
```
]
.panel[.panel-name[Gráfico]

```r
australia_economy %>% autoplot(Pop)
```

![](ACA228_ST_06_files/figure-html/unnamed-chunk-7-1.png)
Tendência clara.
]
.panel[.panel-name[Modelo]

```r
modelo <- australia_economy %>%
  model(ETS(Pop ~ error("A") + trend("A")))
report(modelo)
```

```
## Series: Pop 
## Model: ETS(A,A,N) 
##   Smoothing parameters:
##     alpha = 0.9999 
##     beta  = 0.3266366 
## 
##   Initial states:
##      l[0]      b[0]
##  10.05414 0.2224818
## 
##   sigma^2:  0.0041
## 
##       AIC      AICc       BIC 
## -76.98569 -75.83184 -66.68347
```

```r
fore_aus <- modelo %>% forecast(h = 6)
```
**Obs: "A" para aditivo e "M" para multiplativo**
]
.panel[.panel-name[Gráfico]

```r
fore_aus %>% autoplot(australia_economy) +
  geom_line(aes(y = .fitted), color = "red",  data = augment(modelo)) 
```

![](ACA228_ST_06_files/figure-html/unnamed-chunk-9-1.png)
]
]

---

## Tendência não constante

O método de Holt (1957) assume que a tendência é constante ao longo do tempo.

Em 1985, é proposto um método que amortece a tendência. Com este método as equações são definidas como:

`$$\hat{y}_{t+h|t} = l_t + (\phi  + \phi^2 + \cdots + \phi^h) b_t,$$`

`$$l_t = \alpha y_t + (1-\alpha) (l_{t-1} + \phi b_{t-1}),$$`

`$$b_t = \beta ( l_t  - l_{t-1}) + (1 - \beta) \phi b_{t-1}.$$`

Note que se `$\phi = 1$` temos o método de Holt. O **R** estimará esse valor

---

## Tendência não constante

.panelset[
.panel[.panel-name[Dados]

```r
library(fpp3)
australia_economy <- global_economy %>% filter(Country == "Australia") %>% 
  mutate(Pop = Population / 1e6) # População em milhoes 1e6 = 10^6
glimpse(australia_economy)
```

```r
australia_economy %>% autoplot(Pop)
```

![](ACA228_ST_06_files/figure-html/unnamed-chunk-11-1.png)
Tendência clara.
]
.panel[.panel-name[Modelo]

```r
modelo <- australia_economy %>%
  model(holt = ETS(Pop ~ error("A") + trend("A")),
*       amortecimento = ETS(Pop ~ error("A") + trend("Ad")))
modelo %>% select(amortecimento) %>% report()
```

```
## Series: Pop 
## Model: ETS(A,Ad,N) 
##   Smoothing parameters:
##     alpha = 0.9986305 
##     beta  = 0.4271838 
##     phi   = 0.98 
## 
##   Initial states:
##      l[0]      b[0]
##  10.03648 0.2478533
## 
##   sigma^2:  0.0045
## 
##       AIC      AICc       BIC 
## -71.01630 -69.36924 -58.65364
```
**Obs:** "Ad" na tendência para fazer o método de amortecimento.  
]
.panel[.panel-name[Gráfico]

```r
fore_aus <- modelo %>% forecast(h = 6)
fore_aus %>% autoplot(australia_economy, level = NULL) +
  geom_line(aes(y = .fitted), color = "red",  data = augment(modelo)) 
```

![](ACA228_ST_06_files/figure-html/unnamed-chunk-13-1.png)
]
]

---
class: inverse, right, middle
# Case 1

O _dataset_ `WWWusage` do pacote `fpp3` contém informação sobre o número de usuários conectado a uma determinada rede de internet por minuto. Estamos interessados em um modelo para fazer previsão para o próximo minuto.

Utilizaremos os 3 modelos aprendidos até agora e veremos qual nos ajuda a fazer melhores previsões.
---

## Case 1

.panelset[
.panel[.panel-name[Dados]

```r
library(fpp3)
www_usage <- as_tsibble(WWWusage, index = index)
glimpse(www_usage)
```

```
## Rows: 100
## Columns: 2
## $ index <dbl> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 1…
## $ value <dbl> 88, 84, 85, 85, 84, 85, 83, 85, 88, 89, 91, 99, 104, 112, 126, 1…
```
]
.panel[.panel-name[Gráfico]

```r
www_usage %>% autoplot(value)
```

![](ACA228_ST_06_files/figure-html/unnamed-chunk-15-1.png)

]
.panel[.panel-name[Modelos]

```r
# Cross-Validation de tamanho 50 avançando de 1 em 1
www_usage %>% stretch_tsibble(.init = 50, .step = 1) %>%
  model(SES  = ETS(value ~ error("A")),
        Holt = ETS(value ~ error("A") + trend("A")),
        Amortecimento = ETS(value ~ error("A") + trend("Ad"))) %>% 
  forecast(h = 1) %>%
  accuracy(www_usage)
```

```
## Warning: The future dataset is incomplete, incomplete out-of-sample data will be treated as missing. 
## 1 observation is missing at 101
```

```
## # A tibble: 3 × 10
##   .model        .type      ME  RMSE   MAE   MPE  MAPE  MASE RMSSE  ACF1
##   <chr>         <chr>   <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 Amortecimento Test   0.121   3.30  2.78 0.195  2.11 0.614 0.568 0.270
## 2 Holt          Test  -0.0619  3.39  2.94 0.160  2.24 0.651 0.585 0.166
## 3 SES           Test   0.273   3.36  2.88 0.333  2.21 0.637 0.580 0.215
```
Segundo o RMSE e o MAE, qual modelo é melhor?

]

.panel[.panel-name[Modelo Final]
O modelo com amortecimento é o melhor, utilizaremos esse modelo para construir nosso modelo final.

```r
modelo <- www_usage %>%
  model(ETS(value ~ error("A") + trend("Ad")))
report(modelo)
```

```
## Series: value 
## Model: ETS(A,Ad,N) 
##   Smoothing parameters:
##     alpha = 0.9999 
##     beta  = 0.9966439 
##     phi   = 0.814958 
## 
##   Initial states:
##      l[0]        b[0]
##  90.35177 -0.01728234
## 
##   sigma^2:  12.2244
## 
##      AIC     AICc      BIC 
## 717.7310 718.6342 733.3620
```
]

.panel[.panel-name[Gráfico]

```r
fore_www <- modelo %>% forecast(h = 10)
fore_www %>% autoplot(www_usage, level = NULL) +
  geom_line(aes(y = .fitted), color = "red",  data = augment(modelo))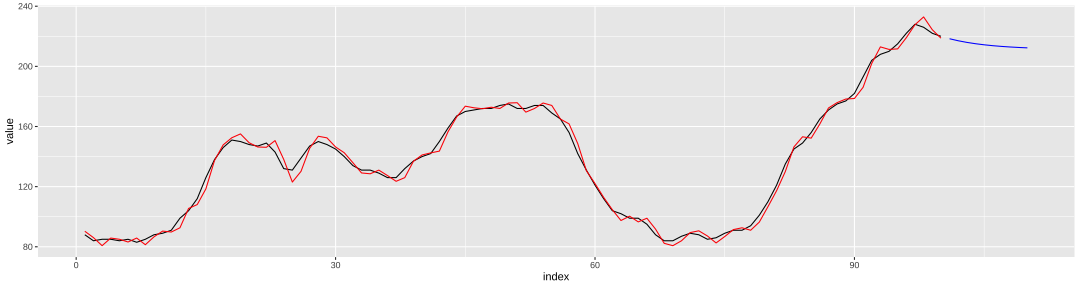 
```

![](ACA228_ST_06_files/figure-html/unnamed-chunk-18-1.png)
]
]

---
class: inverse, right, middle
# Método de Holt-Winters
---

## Método de Holt-Winters

Muitas vezes, a série temporal além de possuir tendência, possui também sazonalidade. Para lidar com estas características, temos o modelo de Holt-Winters, que é uma extensão do método de Holt. Seja `$m$` o período sazonal, então

.pull-left[

**Holt-Winters Aditivo**

`$$\hat{y}_{t+h|t} = l_t + hb_t + s_{t+h-m(k+1)},$$`

`$$l_t = \alpha (y_t - s_{t-m}) + (1-\alpha) (l_{t-1}+  b_{t-1}),$$`

`$$b_t = \beta (l_t - l_{t-1}) + (1-\beta) b_{t-1},$$`

`$$s_t = \gamma (y_t - l_{t-1} - b_{t-1}) + (1-\gamma) s_{t-m}.$$`
Em que `$k$` é a parte inteira de `$(h-1)/m$`.

]

.pull-right[

**Holt-Winters Multiplicativo**

`$$\hat{y}_{t+h|t} = (l_t + hb_t)s_{t+h-m(k+1)},$$`

`$$l_t = \alpha \dfrac{y_t}{s_{t-m}} + (1-\alpha) (l_{t-1} + b_{t-1}),$$`

`$$b_t = \beta (l_t - l_{t-1}) + (1-\beta) b_{t-1},$$`

`$$s_t = \gamma \dfrac{y_t}{l_{t-1} + b_{t-1}} + (1-\gamma) s_{t-m}$$`
]

Se a variação sazonal é constante utilizamos o modelo aditivo, caso contrário o multiplicativo.

```r
error("A") + trend("A") + season("A")  # Quando Aditivo
error("M") + trend("A") + season("M")  # Quando Multiplicativo
```

---

## Método de Holt-Winters

.panelset[
.panel[.panel-name[Dados]

```r
library(fpp3)
library(dplyr)
glimpse(tourism)
```

```
## Rows: 24,320
## Columns: 5
## Key: Region, State, Purpose [304]
## $ Quarter <qtr> 1998 Q1, 1998 Q2, 1998 Q3, 1998 Q4, 1999 Q1, 1999 Q2, 1999 Q3,…
## $ Region  <chr> "Adelaide", "Adelaide", "Adelaide", "Adelaide", "Adelaide", "A…
## $ State   <chr> "South Australia", "South Australia", "South Australia", "Sout…
## $ Purpose <chr> "Business", "Business", "Business", "Business", "Business", "B…
## $ Trips   <dbl> 135.0777, 109.9873, 166.0347, 127.1605, 137.4485, 199.9126, 16…
```

```r
aus_holidays <- tourism %>% 
  filter(Purpose == "Holiday") %>%
  summarise(Trips = sum(Trips)/1000) #Agrupamos por Quarter e os valores em mil unidades.  
```

]
.panel[.panel-name[Gráfico]

```r
aus_holidays %>% autoplot(Trips)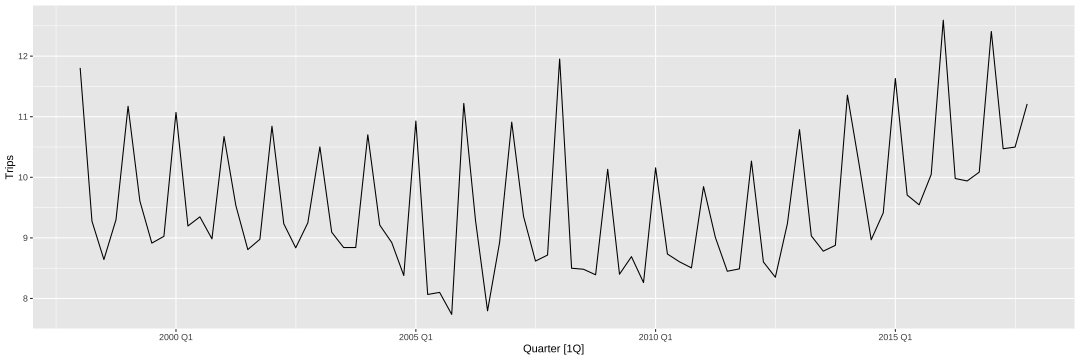
```

![](ACA228_ST_06_files/figure-html/unnamed-chunk-21-1.png)

]
.panel[.panel-name[Modelos]

```r
# Cross-Validation de tamanho 50 avançando de 1 em 1
aus_holidays %>% stretch_tsibble(.init = 50, .step = 1) %>%
  model(HWA = ETS(Trips ~ error("A") + trend("A") + season("A")),
        HWM = ETS(Trips ~ error("M") + trend("A") + season("M"))) %>% 
  forecast(h = 4) %>%
  group_by(.id) %>%
  mutate(h = row_number()) %>%
  ungroup() %>% 
  accuracy(aus_holidays, by = c("h", ".model"))
```

```
## Warning: The future dataset is incomplete, incomplete out-of-sample data will be treated as missing. 
## 4 observations are missing between 2018 Q1 and 2018 Q4
```

```
## # A tibble: 8 × 11
##       h .model .type    ME  RMSE   MAE   MPE  MAPE  MASE RMSSE  ACF1
##   <int> <chr>  <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1     1 HWA    Test  0.264 0.474 0.361  2.68  3.64 0.870 0.878 0.133
## 2     2 HWA    Test  0.302 0.499 0.381  3.02  3.82 0.918 0.925 0.305
## 3     3 HWA    Test  0.372 0.548 0.444  3.76  4.46 1.07  1.01  0.284
## 4     4 HWA    Test  0.449 0.586 0.466  4.50  4.65 1.12  1.09  0.421
## 5     5 HWM    Test  0.270 0.462 0.361  2.77  3.66 0.871 0.857 0.204
## 6     6 HWM    Test  0.312 0.503 0.394  3.14  3.93 0.950 0.932 0.319
## 7     7 HWM    Test  0.360 0.545 0.448  3.63  4.48 1.08  1.01  0.378
## 8     8 HWM    Test  0.434 0.598 0.480  4.37  4.76 1.16  1.11  0.425
```
]
.panel[.panel-name[Modelo Final]

```r
# Como nenhum modelo parece ser superior ao outro
modelo <- aus_holidays %>%
  model(HWA = ETS(Trips ~ error("A") + trend("A") + season("A")),
        HWM = ETS(Trips ~ error("M") + trend("A") + season("M")))
fore_trips <- modelo %>% forecast(h = 4)
```
]
.panel[.panel-name[Previsão]

```r
fore_trips %>% autoplot(aus_holidays, level = NULL)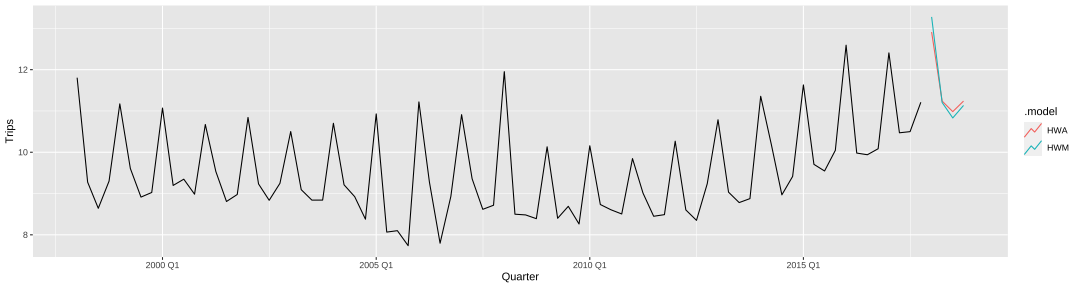
```

![](ACA228_ST_06_files/figure-html/unnamed-chunk-24-1.png)
]
]

---

## Método de Holt-Winters

Se quisermos incluir o amorcetimento na componente de tendência, basta trocar

```r
trend("A")
```
por

```r
trend("Ad")
```
nos códigos do slide anterior.

---

## Exercício

O _dataset_ referente à temperatura de Lajeado/RS está disponível [aqui](https://raw.githubusercontent.com/ctruciosm/ctruciosm.github.io/master/datasets/lajeado_rs.csv).

Estamos interessados em fazer a previsão 1 mês à frente da temperatura média.

- Utilizando validação cruzada (considere `.init = 45` e `.step = 1`), teste os seguintes métodos: NAIVE, MEDIA, SNAIVE, Regressão Linear (com tendência e sazonalidade), Drift, Holt-Winters Aditivo e Holt-Winter Aditivo com amortecimento).
- Escolha o melhor (ou um dos melhores) modelo segundo os resultados do RMSE ou MAE.
- Com o modelo final escolhido faça previsão 1 passo à frente e faça o gráfico correspondente.

> Entregar até antes da próxima aula.

---

### Referências

- [Hyndman, R.J., & Athanasopoulos, G. (2021). Forecasting: principles and practice, 3rd edition, OTexts: Melbourne, Australia. OTexts.com/fpp3.](https://otexts.com/fpp3/). Chapter 8.1--8.3.