class: center, middle, inverse, title-slide # Modelos de Regressão e Previsão (ACA228) ## Introdução aos modelos de previsão ### Prof. Carlos Trucíos <br><a href="http://ctruciosm.github.io"> <i class="fa fa-desktop fa-fw"></i>  ctruciosm.github.io</a><br> <a href="mailto:carlos.trucios@facc.ufrj.br"><i class="fa fa-paper-plane fa-fw"></i>  carlos.trucios@facc.ufrj.br</a><br> ### Faculdade de Administração e Ciências Contábeis, </br> Universidade Federal de Rio de Janeiro --- layout: true <a class="footer-link" href="http://ctruciosm.github.io">ctruciosm.github.io &mdash; Carlos Trucíos (FACC/UFRJ)</a> --- <div> <style type="text/css">.xaringan-extra-logo { width: 200px; height: 350px; z-index: 0; background-image: url(imagens/UFRJ.png); background-size: contain; background-repeat: no-repeat; position: absolute; top:1em;right:1em; } </style> <script>(function () { let tries = 0 function addLogo () { if (typeof slideshow === 'undefined') { tries += 1 if (tries < 10) { setTimeout(addLogo, 100) } } else { document.querySelectorAll('.remark-slide-content:not(.title-slide):not(.inverse):not(.hide_logo)') .forEach(function (slide) { const logo = document.createElement('div') logo.classList = 'xaringan-extra-logo' logo.href = null slide.appendChild(logo) }) } } document.addEventListener('DOMContentLoaded', addLogo) })()</script> </div> ## Introdução .bg-washed-green.b--dark-green.ba.bw2.br3.shadow-5.ph4.mt5[ Se pudéssemos saber primeiro onde estamos e para onde estamos indo, poderíamos julgar melhor o que fazer e como fazê-lo. .tr[ — Abraham Lincoln ]] -- O interesse em fazer previsão existe em muitas situações: prever a demanda de um produto, prever a quantidade de megas que serão utilizados mos próximos dias, prever o preço das ações, prever o clima, etc. -- A previsibilidade de um evento ou quantidade, depende de vários fatores, entre eles: - Quantos dados estão disponíveis. - Que tanto conhecemos os fatores que contribuen para fazer a previsão. - Que tão semelhante é o futuro do passado. - Se a previsão afeta o que estamos tentanto prever. -- > Previsão pode ser feita utilizando métodos ingênuos (como repetir a última observação) ou métodos mais complexos (como métodos estatísticos avançados e redes neurais) --- ## Introdução Previsão ajuda às organizações a tomarem melhores decisões e fornece uma guia para o planejamento de médio e longo prazo. -- .red[ `$$\text{Previsão} \neq \text{Metas} \neq \text{Planejamento}$$`] -- - **Previsão:** dadas todas as informações disponíveis (historico, outras variáveis, conhecimento sobre eventos futuro que possam afetar a previsão), .blue[prever o futuro com a maior acurácia possível.] -- - **Metas:** aquilo que gostariamos que aconteça (mas elas não necessáriamente acontecem) -- - **Planejamento:** ações necessárias para que nossas previsões alcancem as metas. -- Estamos interessados em previsões a: - curto prazo - médio prazo - longo prazo -- > Embora existam métodos qualitativos para fazer previsão quando não temos historico de dados, focaremos no caso em que possuimos um conjunto de dados históricos e é razoável pensar que algums padrões aprendidos do passado continurão acontecendo. --- class: inverse, right, middle # Séries Temporais --- ## Séries Temporais **Séries temporal:** todo processo que é observado sequencialmente ao longo do tempo é uma série temporal. -- .pull-left[ **Exemplos** - Produto interno bruto (anual) do Brasil - Preço diário do Bitcoin - Vendas semanais - Temperatura diária - Consumo mensal de energia/agua - etc ] -- .pull-right[ 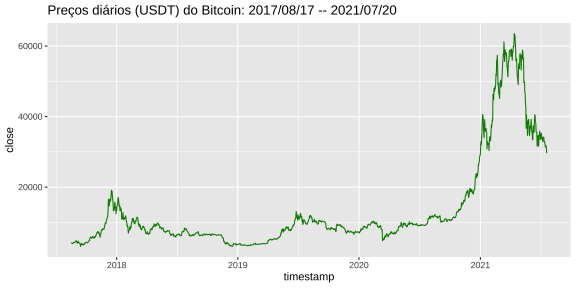<!-- --> ] -- > Quando falamos em previsão, o objetivo é estimar como a sequência de observações (observadas cronologicamente) continuará no futuro. --- # Séries Temporais .center[ <!-- --> ] -- `$$y_t = f(X_{1}, \cdots, X_{k}, u)$$` -- `$$y_t = f(y_{t-1}, \cdots, y_{t-r}, u)$$` -- `$$y_t = f(y_{t-1}, \cdots, y_{t-r}, X_1, \cdots, X_k, u)$$` --- class: inverse, right, middle # Decomposição das Séries Temporais --- ## Decomposição das Séries Temporais .bg-washed-green.b--dark-green.ba.bw2.br3.shadow-5.ph4.mt5[ Assume que a série temporal pode ser decomposta em: - Componente de tendência (ou tendência-ciclo): `\(T_t\)` - Componente Sazonal: `\(S_t\)` - Componente aleatória ou _resto_ ou _irregular_: `\(a_t\)` (ou `\(R_t\)` ou `\(I_t\)`). `$$y_t = \underbrace{T_t + S_t + a_t}_{\text{Modelo Aditivo}} \quad \text{ou} \quad y_t = \underbrace{T_t \times S_t \times a_t}_{\text{Modelo Multiplicativo}}$$`] -- - **Tendência:** Componente a longo prazo e indica um aumento/diminuição. - **Sazonalidade:** Oscilações que se produzem e repetem em curtos períodos de tempo (semanal, mensal, trimestral,...) - **Aleatoriedade:** A parte que não é explicada pelas componentes anteriores. --- ## Decomposição das Séries Temporais > Se as flutuações sazonais em torno da tendência não variam com o nível da série, estamos ante um **modelo aditivo**. Já se as flutuações sazonais em torno da tendência parecem ser proporcionais com o nível da série, estamos ante um **modelo multiplicativo**. -- 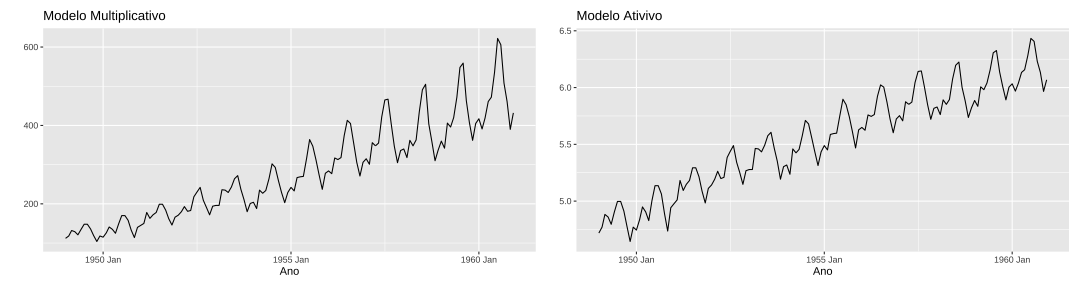<!-- --> -- > Aprenderemos várias técnicas para estimar essas componentes. --- class: inverse, right, middle # Médias Móveis (MM) --- ## Médias Móveis (1920s) É um dos métodos mais clássicos para estimar `\(T_t\)`. `$$\hat{T}_t = \dfrac{1}{m}\displaystyle \sum_{i=-k}^k y_{t+i},$$`em que `\(m = 2k+1\)` e a média movel é dita de ordem `\(m\)` (ou `\(m\)`-MM) -- | tempo| y| |-----:|---:| | 2005| 105| | 2006| 109| | 2007| 111| | 2008| 116| | 2009| 121| | 2010| 126| | 2011| 129| | 2012| 134| | 2013| 138| | 2014| 143| | 2015| 147| | 2016| 151| | 2017| 154| | 2018| 158| | 2019| 162| | 2020| 166| --- ## Médias Móveis (1920s) .panelset[ .panel[.panel-name[Dataset] O _dataset_ `global_economy` do pacote `fpp3` possui informação econômica de 263 países desde 1960 até 2017. ``` ## Rows: 15,150 ## Columns: 9 ## Key: Country [263] ## $ Country <fct> "Afghanistan", "Afghanistan", "Afghanistan", "Afghanistan",… ## $ Code <fct> AFG, AFG, AFG, AFG, AFG, AFG, AFG, AFG, AFG, AFG, AFG, AFG,… ## $ Year <dbl> 1960, 1961, 1962, 1963, 1964, 1965, 1966, 1967, 1968, 1969,… ## $ GDP <dbl> 537777811, 548888896, 546666678, 751111191, 800000044, 1006… ## $ Growth <dbl> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA,… ## $ CPI <dbl> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA,… ## $ Imports <dbl> 7.024793, 8.097166, 9.349593, 16.863910, 18.055555, 21.4128… ## $ Exports <dbl> 4.132233, 4.453443, 4.878051, 9.171601, 8.888893, 11.258279… ## $ Population <dbl> 8996351, 9166764, 9345868, 9533954, 9731361, 9938414, 10152… ``` Selecionaremos unicamente os dados para o Brasil e calcularemos a média móvel para a variável `Exports`. ] .panel[.panel-name[MM] Para calcular a média móvel, utilizamos a função `slide_dbl` do pacote `slider`. ```r library(fpp3) # contém o dataset global_economy library(slider) # para calcular as MM de forma fácil br_export <- global_economy %>% filter(Country == "Brazil") %>% mutate(MM5 = slide_dbl(Exports, mean,.before = 2, .after = 2, .complete = TRUE)) ``` ] .panel[.panel-name[MM-Dataset] ```r tail(br_export) ``` ``` ## # A tsibble: 6 x 10 [1Y] ## # Key: Country [1] ## Country Code Year GDP Growth CPI Imports Exports Population MM5 ## <fct> <fct> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> ## 1 Brazil BRA 2012 2.47e12 1.93 112. 13.1 11.7 200560983 11.3 ## 2 Brazil BRA 2013 2.47e12 3.01 119. 13.9 11.6 202408632 11.7 ## 3 Brazil BRA 2014 2.46e12 0.508 127. 13.7 11.0 204213133 11.9 ## 4 Brazil BRA 2015 1.80e12 -3.55 138. 14.1 12.9 205962108 12.1 ## 5 Brazil BRA 2016 1.79e12 -3.47 150. 12.1 12.5 207652865 NA ## 6 Brazil BRA 2017 2.06e12 0.976 156. 11.6 12.6 209288278 NA ``` ] .panel[.panel-name[Gráfico] .left-column[ GDP (Gross Domestic Product) `\(\equiv\)` PIB ] .right-column[ 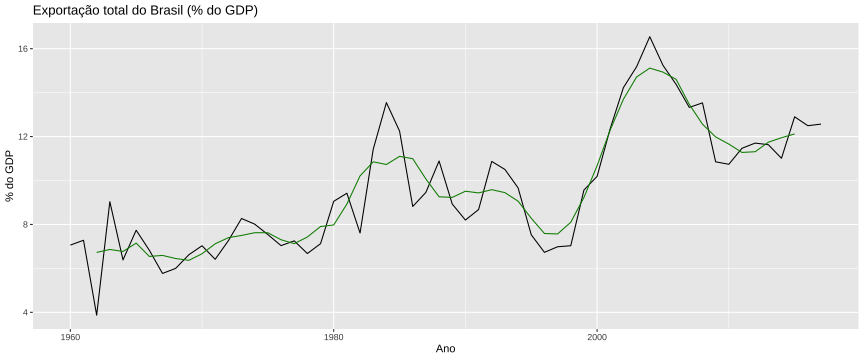<!-- --> ] ] .panel[.panel-name[Código completo] ```r library(fpp3) # contém o dataset global_economy library(slider) # para calcular as MM de forma fácil library(ggplot2) # Para fazer os gráficos br_export <- global_economy %>% filter(Country == "Brazil") %>% mutate(MM5 = slide_dbl(Exports, mean,.before = 2, .after = 2, .complete = TRUE)) ggplot(br_export) + geom_line(aes(x = Year, y = Exports)) + geom_line(aes(x = Year, y = MM5), color = "green4") + ylab("% do GDP") + xlab("Ano") + ggtitle("Exportação total do Brasil (% do GDP)") ``` ] ] --- ## Médias Móveis (1920s) - A MM `suaviza` a série original e captura os principais movimentos da série - O valor de `\(m\)` determina quão suavizada será a série. -- <!-- --> > Modificações de MM como `Média Móvel da Média Móvel` e `Média Móvel Ponderada` são também úteis. --- class: inverse, right, middle # Método Clássico de Decomposição --- ## Método Clássico de Decomposição .pull-left[ #### Modelo Aditivo `$$y_t = T_t + S_t + R_t$$` - **Passo 1:** Estimar `\(T_t\)` (ou seja calcular `\(\hat{T}_t\)`) através do método de médias móveis. - **Passo 2:** Calcular `\(y_t - \hat{T}_t\)` (tiramos o efeito da tendência) - **Passo 3:** Estimar `\(S_t\)` (ou seja calcular `\(\hat{S}_t\)`) através da média das `\(y_t - \hat{T}_t\)` para esse ponto sazonal. (Ex: se trabalharmos com dados mensais, calcular a média de todas as observações em Janeiro, depois Fevereiro, ....) - **Passo 4:** Calcular `\(\hat{R}_t = y_t - \hat{T}_t - \hat{S}_t\)` ] -- .pull-right[ #### Modelo Multiplicativo `$$y_t = T_t \times S_t \times R_t$$` - **Passo 1:** Estimar `\(T_t\)` (ou seja calcular `\(\hat{T}_t\)`) através do método de médias móveis. - **Passo 2:** Calcular `\(y_t/\hat{T}_t\)` (tiramos o efeito da tendência) - **Passo 3:** Estimar `\(S_t\)` (ou seja calcular `\(\hat{S}_t\)`) através da média das `\(y_t - \hat{T}_t\)` para esse ponto sazonal. (Ex: se trabalharmos com dados mensais, calcular a média de todas as observações em Janeiro, depois Fevereiro, ....) - **Passo 4:** Calcular `\(\hat{R}_t = y_t/(\hat{T}_t \times \hat{S}_t)\)` ] --- ## Método Clássico de Decomposição .panelset[ .panel[.panel-name[Importando dados] ```r # Importando dados library(tsibble) # Para trabalhar com séries temporais library(dplyr) url <- "https://raw.githubusercontent.com/jbrownlee/Datasets/master/airline-passengers.csv" passageiros <- read.csv(url) glimpse(passageiros) # R ainda não sabe que nossos dados são de séries temporais ``` ``` ## Rows: 144 ## Columns: 2 ## $ Month <chr> "1949-01", "1949-02", "1949-03", "1949-04", "1949-05", "194… ## $ Passengers <int> 112, 118, 132, 129, 121, 135, 148, 148, 136, 119, 104, 118,… ``` ```r passageiros <- passageiros %>% mutate(Month = yearmonth(Month)) %>% as_tsibble(index = Month) glimpse(passageiros) # Agora R sabe sim! ``` ``` ## Rows: 144 ## Columns: 2 ## $ Month <mth> 1949 Jan, 1949 Fev, 1949 Mar, 1949 Abr, 1949 Mai, 1949 Jun,… ## $ Passengers <int> 112, 118, 132, 129, 121, 135, 148, 148, 136, 119, 104, 118,… ``` outras funções úteis do pacote `tsibble` são `yearquarter()`, `yearweek()`, `as_date()`, `ymd()`, `ymd_hms()`. ] .panel[.panel-name[Gráfico] ```r ggplot(passageiros) + geom_line(aes(x = Month, y = Passengers)) ``` <!-- --> ] .panel[.panel-name[Decomposição] ```r passageiros %>% # passageiros é do tipo tsibble * model(classical_decomposition(Passengers, type = "multiplicative")) %>% components() %>% # extraimos as componentes T_t, S_t e R_t autoplot() ``` `type` pode ser "multiplicative" ou "aditive" dependendo do tipo de decomposição. ] .panel[.panel-name[Decomposição-Gráfico] <!-- --> ] ] --- class: inverse, right, middle # Outros Métodos de Decomposição --- ## Outros Métodos de Decomposição O **método clássico de decomposição** possui algumas limitações que fazem dele um método pouco recomendado nos dias de hoje: - Como utilizamos médias móveis, a componente de tendência não possui valores nas primeiras nem últimas observações. - A componente sazonal `\(S_t\)` é obtida assumindo que é constante. - Não é possível obter valores de `\(\hat{R}_t\)` para as primeiras ou últimas observações. - Não é robusto a observações atípicas. -- > Outros métodos de decomposição como **X-11**, **SEATS** (Seasonal Extraction in ARIMA Time Series) e **STL** (Seasonal and Trend decomposition using Loess), resolvem algumas das frequezas encontradas no método clássico. --- ## Outros Métodos de Decomposição .panelset[ .panel[.panel-name[Método X-11] - Desenvolvido pelo US Census Bureau. - Baseado no modelo clássico, mas inclui outras etapas para superar as limitações do método original (a componente de tendência está disponível para todas as observações, a componente sazonal pode variar suavemente, etc). - Existem versões tanto para o modelo aditivo quanto para o multiplicativo. - É robusto a outliers. > **Importante:** Desenhando para dados mensais e quatrimestrais. ] .panel[.panel-name[Código] ```r library(seasonal) library(tsibble) library(fpp3) passageiros %>% * model(X_13ARIMA_SEATS(Passengers ~ x11())) %>% components() %>% autoplot() ``` `X_13ARIMA_SEATS` chama funções do pacote `seasonal` ] .panel[.panel-name[Gráfico] <!-- --> `X_13ARIMA_SEATS` chama funções do pacote `seasonal` ] ] --- ## Outros Métodos de Decomposição .panelset[ .panel[.panel-name[Método SEATS] - Desenvolvido pelo banco de Espanha. - Muito utilizado por agências governamentais no mundo todo. - Desenhando para dados mensais e quatrimestrais. ] .panel[.panel-name[Código] ```r library(seasonal) passageiros %>% * model(X_13ARIMA_SEATS(Passengers ~ seats())) %>% components() %>% autoplot() ``` `X_13ARIMA_SEATS` chama funções do pacote `seasonal` ] .panel[.panel-name[Gráfico] <!-- --> ] ] --- ## Outros Métodos de Decomposição .panelset[ .panel[.panel-name[Método STL] STL (Seasonal and Trend decomposition using Loess) - Desenvolvido por Cleveland (1990) - Funciona com qualquer tipo de sazonalidade (não apenas mensal ou quatrimestral) - A componente sazonal pode mudar ao longo do tempo. - É robusto a observações atípicas - Útil para modelos **aditivos** - Se quisermos aplicar o método em modelos multiplicativos, podemos aplicar um `\(\log(\cdot)\)`. `$$Y_t = T_t \times S_t \times R_t$$` `$$\log(Y_t) = \log(T_t) + \log(S_t) + \log(R_t)$$` ] .panel[.panel-name[Código] ```r passageiros %>% * model(STL(log(Passengers) ~ trend() + season(), robust = TRUE)) %>% components() %>% autoplot() ``` ] .panel[.panel-name[Gráfico] <!-- --> ] ] --- ## Previsão e decomposição > Métodos de decomposição são geralmente utilizados para entender a dinâmica da série mas também podem ser utilizados para fazer previsão. Dependendo se o modelo for aditivo ou multiplicativo, podemos escrever a série temporal como. `$$y_t = \hat{S}_t + \underbrace{\hat{T}_t + \hat{R_t}}_{\hat{A}_t}\quad \text{ou} \quad y_t = \hat{S}_t \times \underbrace{\hat{T}_t \times \hat{R_t}}_{\hat{A}_t},$$` em que `\(\hat{A}_t\)` é a série ajustada pela sazonalidade. Para fazer previsão da série original, fazemos previsão da componente sazonal `\(\hat{S}_t\)` e da série ajustada pela sazonalidade `\(\hat{A}_t\)` de forma independente e depois combinamos ambas previsões para obter a previsão da série original. -- - Comumente, um método ingênuo (naive) é utilizado para prever `\(\hat{S}_t\)` (utilizamos os valores de `\(\hat{S}_t\)` no último ano). - Para prever `\(\hat{A}_t\)` utilizamos métodos para dados não sazonais (que veremos nas próximas aulas) como o método de Holt, ARIMA, etc. --- ## Exercícios. 1. Utilize o _dataset_ `global_economy` do pacote `fpp3` e aplique o método de médias moveis de ordem 7 na variável GDP. (Faça também o gráfico correspondente incluindo a série original e a série suavizada por MM7) 2. Utilize a variável `Electricity` do _dataset_ `aus_production` disponível no pacote `fpp3` e aplique os métodos de decomposição * clássico * X-11 * SEATS * LTS -- > **Entregar até antes da próxima aula** (enviar o código pelo Google Class) --- ### Referências - [Hyndman, R.J., & Athanasopoulos, G. (2021) Forecasting: principles and practice, 3rd edition, OTexts: Melbourne, Australia. OTexts.com/fpp3.](https://otexts.com/fpp3/). Chapters 1--3 --